For two springs connected in series, the effective spring factor is …………. than the individual spring factor of each spring.
To find the effective spring factor for two springs connected in series, we can follow these steps:
Step 1: Understand the Concept of Spring Constants
- Each spring has a spring constant (k), which measures its stiffness. A higher spring constant means a stiffer spring.
Step 2: Define the Spring Constants
- Let the spring constants of the two springs be k1 and k2.
Step 3: Use the Formula for Springs in Series
- When two springs are connected in series, the effective spring constant kequiv can be calculated using the formula:
1kequiv=1k1+1k2
Step 4: Rearrange the Formula
- Rearranging the formula gives:
kequiv=k1k2k1+k2
Step 5: Analyze the Result
- The effective spring constant kequiv is a fraction of the product of k1 and k2 divided by their sum. This means that kequiv will always be less than either k1 or k2 unless both springs have the same spring constant.
Conclusion
- Therefore, we conclude that for two springs connected in series, the effective spring factor is less than the individual spring factor of each spring.
---
- Each spring has a spring constant (k), which measures its stiffness. A higher spring constant means a stiffer spring.
- Let the spring constants of the two springs be k1 and k2.
- When two springs are connected in series, the effective spring constant kequiv can be calculated using the formula:
1kequiv=1k1+1k2
- Rearranging the formula gives:
kequiv=k1k2k1+k2
- The effective spring constant kequiv is a fraction of the product of k1 and k2 divided by their sum. This means that kequiv will always be less than either k1 or k2 unless both springs have the same spring constant.
- Therefore, we conclude that for two springs connected in series, the effective spring factor is less than the individual spring factor of each spring.
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Revision Exercises (Short Answer Questions)
24 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Revision Exercises (Long Answer Questions)
5 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Revision Exercises (Additional Question )
3 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
Knowledge Check
A mass m is suspended from the two coupled springs connected in series. The force constant for spring are k1 and k2. The time period of the suspended mass will be:
AT=2π√mk1−k2BT=2π√mk1k2k1+k2CT=2π√mk1+k2DT=2π√m(k1+k2)k1k2If two similar springs each of spring constant K1 are joined in series, the new spring constant and time period would be changed by a factor:
A12,√2B14,√2C14,2√2D12,√2Two springs of spring constantsK1 and K2 are joined in series. The effective spring constant of the combination is given by
A√k1k2B(k1+k2)2Ck1+k2Dk1k2(k1+k2)
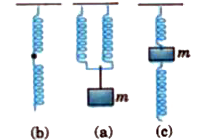
Two identical springs, each of spring factor k, may be connected in the following ways. Deduce the spring factor of the oscillation of the body in each case.
View SolutionTwo identical springs (springs constant K) are connected together in three different ways. In which case will the spring factor of the oscillation of the body be least ?
View SolutionSpring force and cutting OF springs
View SolutionTwo spring of spring constant k1 and k2 are joined in series The effective spring constant of the combination is given by
View SolutionThe effective spring constant of two spring system as shown in figure will be

View Solution
