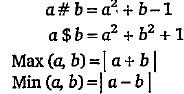a#b=a2+b−1
a$b=a2+b2+1
Max (a,b)=|a+b|
Min (a, b)=|a−b|
Max [(2#3)$(3#4),(4$4)] is equal to :
a. 1234
b. 1236
c. 1335
d. none of these
The correct Answer is:D
To solve the problem step by step, we need to evaluate the expressions given in the question using the defined operations. Let's break it down:
Step 1: Calculate 2#3
The operation a#b is defined as:
a#b=a2+b−1
Substituting a=2 and b=3:
2#3=22+3−1
Calculating:
=4+3−1=6
Step 2: Calculate 3#4
Using the same operation a#b:
3#4=32+4−1
Calculating:
=9+4−1=12
Step 3: Calculate 4$4
The operation a$b is defined as:
a$b=a2+b2+1
Substituting a=4 and b=4:
4$4=42+42+1
Calculating:
=16+16+1=33
Step 4: Calculate 6$12
Now we need to evaluate (2#3)$(3#4), which is 6$12:
6$12=62+122+1
Calculating:
=36+144+1=181
Step 5: Find the maximum of 181 and 33
Finally, we need to find:
Max(181,33)
Calculating:
=181
Final Answer
Thus, the maximum value is:
181
The operation a#b is defined as:
a#b=a2+b−1
Substituting a=2 and b=3:
2#3=22+3−1
Calculating:
=4+3−1=6
Using the same operation a#b:
3#4=32+4−1
Calculating:
=9+4−1=12
The operation a$b is defined as:
a$b=a2+b2+1
Substituting a=4 and b=4:
4$4=42+42+1
Calculating:
=16+16+1=33
Now we need to evaluate (2#3)$(3#4), which is 6$12:
6$12=62+122+1
Calculating:
=36+144+1=181
Finally, we need to find:
Max(181,33)
Calculating:
=181
Thus, the maximum value is:
181
Topper's Solved these Questions
- BOOK - ARIHANT SSCCHAPTER - FUNCTIONS AND GRAPHEXERCISE - EXERCISE(LEVEL 2)48videos
FUNCTIONS AND GRAPH
- BOOK - ARIHANT SSCCHAPTER - FUNCTIONS AND GRAPHEXERCISE - Final Round40videos
FUNCTIONS AND GRAPH
- BOOK - ARIHANT SSCCHAPTER - FUNCTIONS AND GRAPHEXERCISE - INTRODUCTORY EXERCISE - 17.317videos
FUNCTIONS AND GRAPH
- BOOK - ARIHANT SSCCHAPTER - ELEMENTS OF ALGEBRAEXERCISE - EXERCISE(LEVEL 1)32videos
ELEMENTS OF ALGEBRA
- BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 240videos
FUNDAMENTALS
Similar Questions
Knowledge Check
- Question 1 - Select One
a#b=a2+b−1
a$b=a2+b2+1
Max (a,b)=|a+b|
Min (a, b)=|a−b|
Max [Min (1$2),(2$3)),Max ((3#4),(4#5))] is equal to :A24B40C42Dnone of these - Question 2 - Select One
a#b=a2+b−1
a$b=a2+b2+1
Max (a,b)=|a+b|
Min (a, b)=|a−b|
Find the value of Min [(1#2)$3,4#(5$6)]$ Max (6#7),(7#8)]:A13574B14573C13575D14674 - Question 3 - Select One
If 2a+ba+4b=3, the value of a+ba+2b is equal to
A59B27C43D109
If f(a,b)=a+b2
g(a,b)=a2+b2
h(a,b)=max (a,b)
Find the value of f(g(3,9)),h(−1,1)View SolutionIf a3−b3=208anda−b=4 then (a+b)2−ab is equal to
View SolutionIf a + b = 1, then 'a^(4) + b^(4) - a^(3) - b^(3) – 2a ^(2)b^(2)' + ab is equal to
View SolutionIf a3−b3=208anda−b=4 then (a+b)2−ab is equal to
View SolutionIf a3−b3=208anda−b=4 then (a+b)2−ab is equal to
View Solution