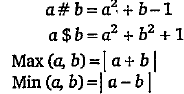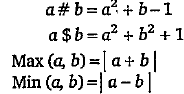![Max [Min (1$2), (2$3), Max ((3#4), (4#5))] is equal to :](https://d10lpgp6xz60nq.cloudfront.net/physics_images/AHT_SKV_QCT_C17_E04_024_Q01.png)
Max [Min (1$2), (2$3), Max ((3#4), (4#5))] is equal to :
A
24
B
40
C
42
D
none of these
Video Solution
Text Solution
The correct Answer is:B
|
Answer
Step by step video & image solution for Max [Min (1$2), (2$3), Max ((3#4), (4#5))] is equal to : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
a#b=a2+b−1
a$b=a2+b2+1
Max (a,b)=|a+b|
Min (a, b)=|a−b|
Max [(2#3)$(3#4),(4$4)] is equal to :Aa. 1234Bb. 1236Cc. 1335Dd. none of thesea#b=a2+b−1
a$b=a2+b2+1
Max (a,b)=|a+b|
Min (a, b)=|a−b|
Find the value of Min [(1#2)$3,4#(5$6)]$ Max (6#7),(7#8)]:A13574B14573C13575D14674The value of [Max(2,4)$Min(6,8)]#[Min(10,12)$Max(14,16)]
A227B225C224Dnone of these
The total number of solution of the equation max(sin,cosx)=12 for x∈(−2π,5π) is equal to
View Solutionlimz→0[{max(sin−1x+cos−1x)2,min(x2+4x+7))}.sin−1zz] is equal to ( where [.] denotes greatest integer function )
View SolutionLet P be a point on the circle |z+2−5i|=6 and A be the point (4 - 3i). Let D = max(AP), then 132D is equal to ____________.
View SolutionIf f(x,y)=(max(x,y))min(x,y) and g(x,y)=max(x,y)−min(x,y), then f(g(−1,−32),g(−4,−1.75)) equals
View SolutionIf f(x,y)=max(x,y)+min(x,y) and g(x,y)=max(x,y)−min(x,y) then the value of f(g(−23,−32),g(−3,−4)) is greater than
View Solution