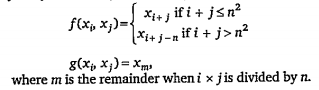The following functions are defined for the set of variables x1,x2,x3,...xn
f(xi,xj)={xi+jifj≤n2xi+j−nifi+j>n2
g(xi,xj)=xm,
where m is the remainder when i×j is divided by n.
Find the value of f(f(x2,x3),f(x5,x6) if n=3
A
x5
B
x10
C
x13
D
none of these
Text Solution
The correct Answer is:B
|
Topper's Solved these Questions
- FUNCTIONS AND GRAPHBOOK - ARIHANT SSCCHAPTER - FUNCTIONS AND GRAPHEXERCISE - Final Round
40 Videos
- FUNCTIONS AND GRAPHBOOK - ARIHANT SSCCHAPTER - FUNCTIONS AND GRAPHEXERCISE - EXERCISE(LEVEL 1)
84 Videos
- ELEMENTS OF ALGEBRABOOK - ARIHANT SSCCHAPTER - ELEMENTS OF ALGEBRAEXERCISE - EXERCISE(LEVEL 1)
32 Videos
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 2
40 Videos
Similar Questions
Knowledge Check
The following functions are defined for the set of variables x1,x2,x3,...xn
f(xi,xj)={xi+jifj≤n2xi+j−nifi+j>n2
g(xi,xj)=xm,
where m is the remainder when i×j is divided by n.
Find the value of g(g(x2,x3),g(x7,x8) if n=5Ax1Bx2Cx5Dnone of theseIf the mean of a set of observations x1,x2,…,xn is ¯¯¯X, then the mean of the observations xi+2i,i=1,2,...,n is
A¯x+2B¯x+nC¯x+2nD¯x+n+1Let f(x)=x2+3x−3,x≥0 if in points x1,x2,x3,...xn are so chosed on the x-axis such that
(i) 1nn∑i=1f−1(xi)=f(1nn∑i=1xi)
(ii) n∑i=1f−1(xi)=n∑i=1xi wehre f−1 denots the inverser of f. then mean of x1,x2,x3,....xn is :A1B2C3D4
The means and variance of n observations x1,x2,x3,…xn are 0 and 5 respectively. If n∑i=1x2i=400, then find the value of n
View SolutionLet f(x)=|3−|2−|x−1|∣∣,∀x∈R be not differentiable at x1,x2,x3,….xn , then n∑i=1x2i equal to :
View SolutionIf f:N→N,andx2>x1⇒f(x2)>f(x)∀x1,x2∈Nandf(f(n))=3n∀n∈N, then f(2)= _______.
View SolutionIf f:N→N,andx2>x1⇒f(x2)>f(x)∀x1,x2∈Nandf(f(n))=3n∀n∈N, then f(2)= _______.
View Solutionif f(x)=(a−xn)1n, where a>0andn is a positive integer, then f(f(x))= (i) x3 (ii) x2 (iii) x (iv) −x
View Solution