दो बल (→P+→Q) व (→P−→Q) परस्पर किस कोण पर कार्य करें कि उनका परिणामी √(P2+Q2) हो ?
यदि दो बलों →A व →B का परिणामी R हो तो
R2=A2+B+2ABcosθ
जहाँ θ दोनों बलों में मध्य का कोण है। प्रश्नानुसार,
(P2+Q2)=(→P+→Q)2+(→P−→Q)2+2∣∣→P+→Q∣∣∣∣→P−→Q∣∣cosθ
P2+Q2=P2+Q2+2→P.→Q+P2+Q2−2→P.→Q+2(P2−Q2)cosθ
0=P2+Q2+2(p2−Q2)cosθ
cosθ=−(P2+Q2)2(P2−Q2)
θ=cos−1[Q2+P22(Q2−P2)]
नोट-यहाँ यह अनिवार्य है कि θ एक वास्तविक राशि हो,
अर्थात् ∣∣∣Q2+P22(Q2−P2)∣∣∣≤1 चूँकि |cosθ|≤1∀θ∈R
Topper's Solved these Questions
- BOOK - SCIENCE PUBLICATIONCHAPTER - समतल में गति EXERCISE - NCERT TEXTBOOK PROBLEMS25videos
समतल में गति
- BOOK - SCIENCE PUBLICATIONCHAPTER - समतल में गति EXERCISE - NCERT TEXTBOOK PROBLEMS (अतिरिक्त अभ्यास)7videos
समतल में गति
- BOOK - SCIENCE PUBLICATIONCHAPTER - समतल में गति EXERCISE - विविध प्रश्न (अतिलघुत्तरात्मक प्रश्न)22videos
समतल में गति
- BOOK - SCIENCE PUBLICATIONCHAPTER - मात्रक एवं मापन EXERCISE - आंकिक प्रश्न21videos
मात्रक एवं मापन
- BOOK - SCIENCE PUBLICATIONCHAPTER - सरल रेखा में गति EXERCISE - अन्य महत्त्वपूर्ण प्रश्न आंकिक प्रश्न (एक समान त्वरित गति पर आधारित प्रश्न)19videos
सरल रेखा में गति
Similar Questions
निम्नलिखित भौतिक राशियों में से बतलाइए कि कौम-सी सदिश हैं और कौन-सी अदिश : आयतन, द्रव्यमान, चाल, त्वरण, घनत्व, मोल संख्या, वेग, कोणीय आवृत्ति, विस्थापन, कोणीय वेग।
01:45View Solutionकिसी सदिश में परिमाण व दिशा दोनों होते हैं। क्या दिक्रस्थान में इसकी कोई स्थिति होती है? क्या यह समय के साथ परिवर्तित हो सकता है। क्या दिक्रथान में भिन्न स्थानों पर दो बराबर सदिशों →aव →b का समान भौतिक प्रभाव अवश्य पड़ेगा? अपने उत्तर के समर्थन में उदाहरण दीजिए।
01:55View Solutionदिये गये चित्र में (i) →Aव →B के y- घटक के क्या चिन्ह हैं ? (ii) (→A+→B) के x-घटक तथा y-घटक के क्या चिन्ह हैं?
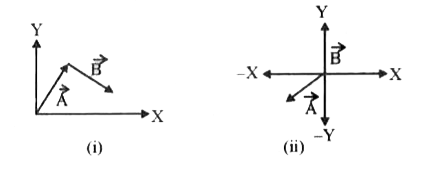 01:53View Solution
01:53View Solutionहवा में ध्वनि का वेग 332 m/s है यदि उसकी लम्बाई को किलोमीटर में तथा समय को घण्टे में नापा जाये तो वेग का नया मान क्या होगा ?
01:56View Solutionएक पिण्ड विरामावस्था से प्रारंभ कर 20मी./से.^2 त्वरण से गति करता है। 6वें सेकण्ड में तय की गई दूरी का मान ज्ञात करो।
03:04View SolutionIf vecP+vecQ=vecR and vecP-vecQ=vecS , prove that vecR^2+vecS^2=2(vecP^2+vecQ^2)
03:12View SolutionIf |vecP + vecQ|= | vecP| -|vecQ| , the angle between the vectors vecP and vecQ is
02:22View Solutionif |vecP + vecQ| = |vecP| + |vecQ| , the angle between the vectors vecP and vecQ is
14:24View SolutionIf |vecP + vecQ| = |vecP -vecQ| the angle between vecP and vecQ is
02:25View Solutionif vecP +vecQ = vecP -vecQ , then
04:09View SolutionIf vecP+vecQ=vecR and |vecP|=|vecQ|=sqrt(3) and |vecR|=3 , then the angle between vecP and vecQ is
04:27View SolutionFor three vectors vecP, vecQ and vecR, vecP+vecQ=vecR and P+Q=R Then prove that vecP and vecQ are parallel to each other.
05:48View SolutionIf →p,→q and →r are perpendicular to →q+→r,→r+→p and →p+→q respectively and if |→p+→q|=6,|→q+→r|=4√3 and |→r+→p|=4 then |→p+→q+→r| is
03:24View SolutionThree vectors →P,→Q,→R obeyP2+Q2=R2 angle between →P & →Q . is
02:53View SolutionTwo vectors →P and →Q are having their magnitudes in the ratio √3:1.Further।→P+→Q।=।→P−→Q। then the angle between the vectors (→P+→Q) and (→P−→Q) is
02:19View Solution

