Find the type of triangle formed by (1,-1), (1,1) and (−√3,√3)Solution in Tamil
Step by step video & image solution for Find the type of triangle formed by (1,-1), (1,1) and (- sqrt(3), sqrt(3)) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COORDINATE GEOMETRYBOOK - FULL MARKSCHAPTER - COORDINATE GEOMETRYEXERCISE - ASSIGNMENT (FILL IN THE BLANKS)
5 Videos
- COORDINATE GEOMETRYBOOK - FULL MARKSCHAPTER - COORDINATE GEOMETRYEXERCISE - ASSIGNMENT (CHOOSE THE CORRECT ANSWER)
7 Videos
- COORDINATE GEOMETRYBOOK - FULL MARKSCHAPTER - COORDINATE GEOMETRYEXERCISE - ADDITIONAL QUESTIONS (MULTIPLE CHOICE QUESTIONS)
15 Videos
- ALGEBRA BOOK - FULL MARKSCHAPTER - ALGEBRA EXERCISE - Assignment Answer the following questions :
1 Videos
- GEOMETRYBOOK - FULL MARKSCHAPTER - GEOMETRYEXERCISE - Assignment (IV. Answer the following questions)
9 Videos
Similar Questions
The abscissa of the origin is ....
View SolutionThe mid point of the line joining (a,-b) and (3a, 5b) is ......
View SolutionOn which quadrant does the point (-4,3) lie ?
View SolutionSubtract 5x2−4y2+6y−3 from 7x2−4xy+5y2+5x−3y
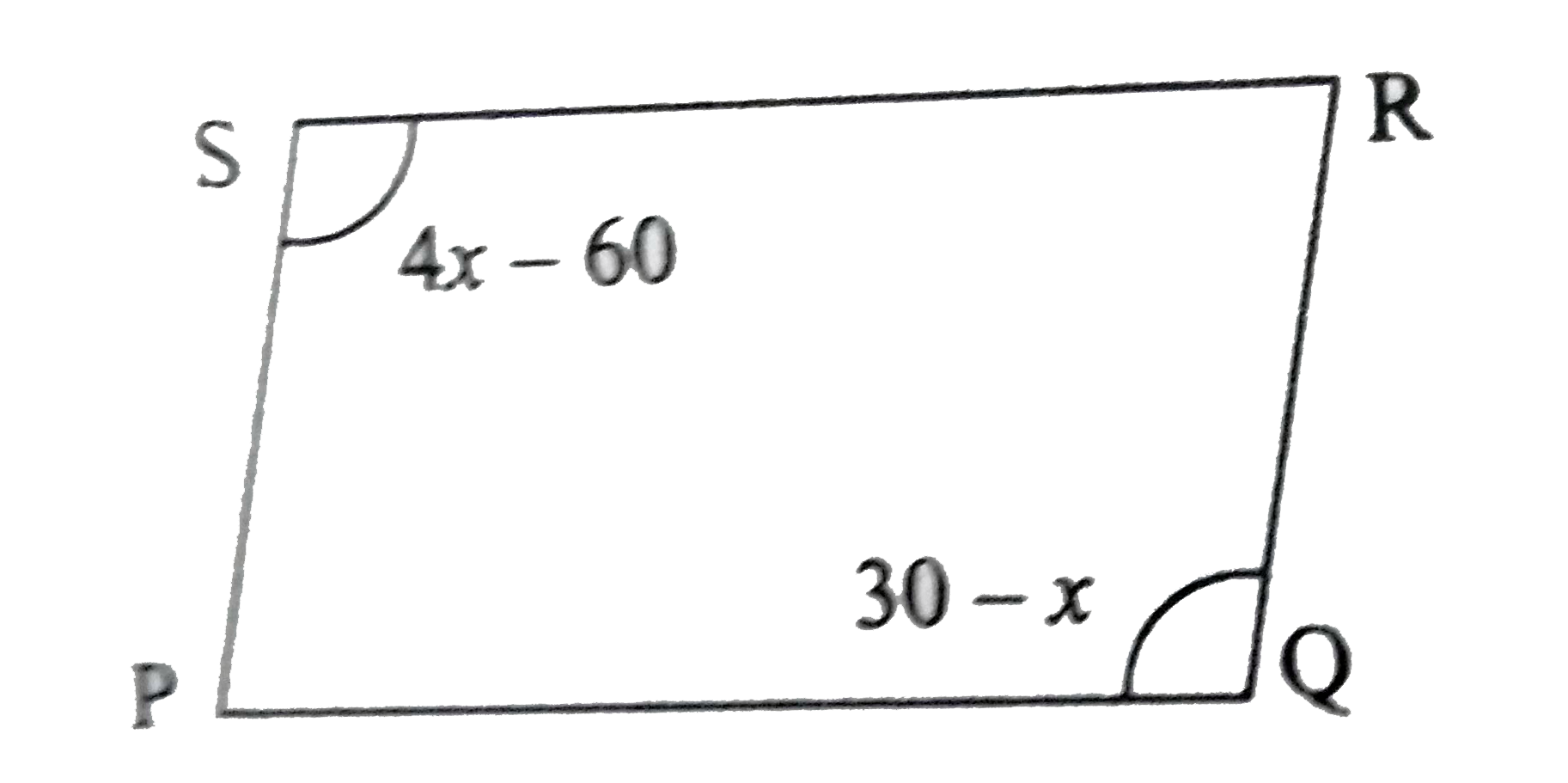
View SolutionIn the given diagram PQRS is a parellelogram.
∠S=4x−60∠Q=30−x. Find the angles of P and R .
View SolutionThe maximum value of Δ=∣∣ ∣∣11111+sinθ11+cosθ11∣∣ ∣∣ is (θ is real) (A) 12 (B) √32 (C) √2 (D) −√32
View SolutionIf the points (1,1),(-1,-1) and (-sqrt(3),k) are vertices of a equilateral triangle then find thevalues of k .
View SolutionThe equation to the base of an equilateral triangle is (sqrt(3)+1)x+(sqrt(3)-1)y+2sqrt(3)=0 and opposite vertex is A(1,1) then the Area of the triangle is
View SolutionFind the type of triangle formed by (1,-1),(-1,1) and (sqrt(3),sqrt(3))
View SolutionFind the unknown parts of ΔABC if a=√3+1,b=√3−1,C=600.
View SolutionIf the points A(1,1), B(-1,-1) and C(−√3,√3) are the vertices of a triangle is
View Solutionसिद्ध कीजिए की बिंदु (1,1)(√3,−√3)व (−1,−1) समबाहु त्रिभुज के शीर्ष है|
View SolutionFind the angles of the triangle whose sides are √3+12√2,√3−12√2 and √32.
View Solutionसिद्ध कीजिए कि बिंदु (1,1),(−1,−1) तथा (−√3,√3) एक समबाहु त्रिभुज के शीर्ष हैं।
View SolutionThe incenter of the triangle with vertices (1,√3),(0,0), and (2,0) is (a)(1,√32) (b) (23,1√3) (c)(23,√32) (d) (1,1√3)
View Solution
