The abscissa of the origin is ....Solution in Tamil
The correct Answer is:0
Step by step video & image solution for The abscissa of the origin is .... by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COORDINATE GEOMETRYBOOK - FULL MARKSCHAPTER - COORDINATE GEOMETRYEXERCISE - ASSIGNMENT (CHOOSE THE CORRECT ANSWER)
7 Videos
- COORDINATE GEOMETRYBOOK - FULL MARKSCHAPTER - COORDINATE GEOMETRYEXERCISE - ASSIGNMENT (ANSWER THE FOLLOWING QUESTIONS)
10 Videos
- COORDINATE GEOMETRYBOOK - FULL MARKSCHAPTER - COORDINATE GEOMETRYEXERCISE - ADDITIONAL QUESTIONS (ANSWER THE FOLLOWING QUESTIONS)
7 Videos
- ALGEBRA BOOK - FULL MARKSCHAPTER - ALGEBRA EXERCISE - Assignment Answer the following questions :
1 Videos
- GEOMETRYBOOK - FULL MARKSCHAPTER - GEOMETRYEXERCISE - Assignment (IV. Answer the following questions)
9 Videos
Similar Questions
The mid point of the line joining (a,-b) and (3a, 5b) is ......
View SolutionRead the coordinates of the vertices of the triangle ABC with the following figure.
View SolutionShow that the given points (1,1) ,(5,4) and (-2,5) are the vertices of an isosceles right angled triangle.
View SolutionSubtract 5x2−4y2+6y−3 from 7x2−4xy+5y2+5x−3y
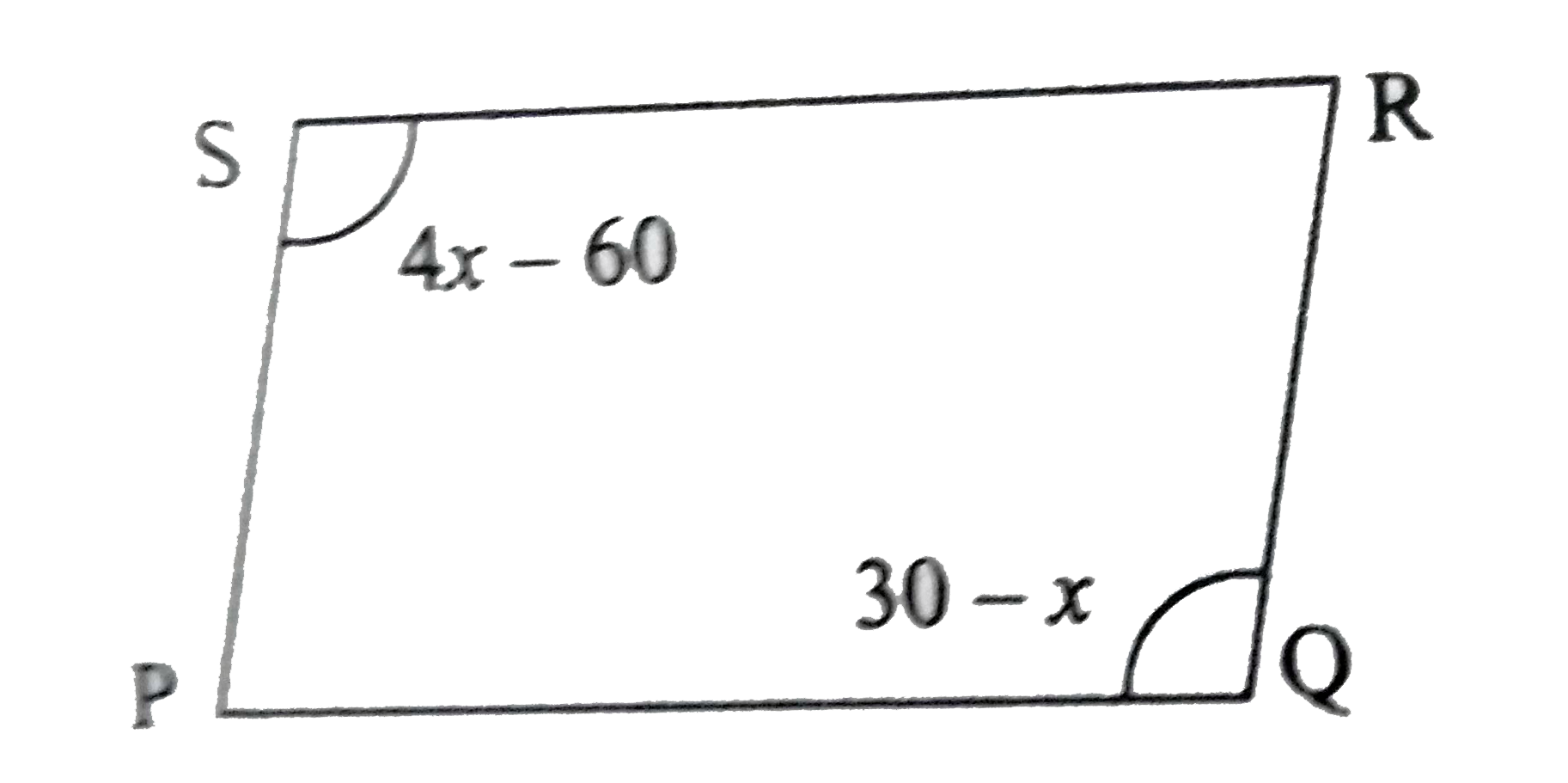
View SolutionIn the given diagram PQRS is a parellelogram.
∠S=4x−60∠Q=30−x. Find the angles of P and R .
View SolutionThe point of intersect of the coordinates axes is: (a) ordinate (b) abscissa (c) quadrant (d) origin
View SolutionThe abscissa and ordinate of the origin are (a) (0, 0) (b) (1, 0) (c) (0, 1) (d) (1, 1)
View SolutionThe equation of curve in which portion of y- axis cutoff between origin and tangent varies as cube of abscissa of point of contact is
View SolutionFind the equation of the curve in which the perpendicular from the origin on any tangent is equal to the abscissa of the point of contact.
View SolutionThe point (other than origin) for which abscissa is equal to the ordinate will lie in the quadrant
View SolutionEquation of circle throught origin, having radius 5 and abscissa of centre is (-3) .
View SolutionThe ratio between the length of substangent at any point other than origin on the parabola y2=16ax and the abscissa of that point is
View SolutionThe points (other than origin) for which abscissa is equal to the ordinate will lie in the quadrant
View SolutionThe abscissa of the point on the curve 3y=6x−5x3, the normal at which passes through origin is :
View SolutionThe point of intersect of the coordinates axes is :
(a) ordinate (b) abscissa (c) quadrant (d) origin
View Solution
