The point of intersect of the coordinates axes is :
(a) ordinate
(b) abscissa
(c) quadrant
(d) origin
To solve the question, we need to identify the point of intersection of the coordinate axes.
1. Understanding the Coordinate Axes:
- The coordinate system consists of two axes: the x-axis (horizontal) and the y-axis (vertical).
- These two axes intersect at a specific point.
2. Identifying the Point of Intersection:
- The point where the x-axis and y-axis intersect is known as the origin.
- The coordinates of the origin are (0, 0).
3. Analyzing the Options:
- (a) Ordinate: This refers to the y-coordinate in a point (x, y).
- (b) Abscissa: This refers to the x-coordinate in a point (x, y).
- (c) Quadrant: This refers to the four sections of the coordinate plane.
- (d) Origin: This is the point of intersection of the x-axis and y-axis, which is (0, 0).
4. Conclusion:
- Based on the definitions and our understanding, the correct answer is (d) origin.
Final Answer:
The point of intersection of the coordinate axes is (d) origin.
- The coordinate system consists of two axes: the x-axis (horizontal) and the y-axis (vertical).
- These two axes intersect at a specific point.
- The point where the x-axis and y-axis intersect is known as the origin.
- The coordinates of the origin are (0, 0).
- (a) Ordinate: This refers to the y-coordinate in a point (x, y).
- (b) Abscissa: This refers to the x-coordinate in a point (x, y).
- (c) Quadrant: This refers to the four sections of the coordinate plane.
- (d) Origin: This is the point of intersection of the x-axis and y-axis, which is (0, 0).
- Based on the definitions and our understanding, the correct answer is (d) origin.
The point of intersection of the coordinate axes is (d) origin.
Topper's Solved these Questions
Similar Questions
A, B C and D are the points of intersection with the coordinate axes of the lines ax+by=ab and bx+ay=ab, then
View SolutionThe weight of an object on the surface of the Earth is 40 N. Its weight at a height equal to the radius of the Earth is
View SolutionLet a,b, c and d be non-zero numbers. If the point of intersection of the lines 4ax+2ay+c=0 and 5bx+2by+d=0 lies in the fourth quadrant and is equidistant from the two axes, then
View SolutionFrom the point (2, 2) tangent are drawn to the hyperbola x216−y29=1. Then the point of contact lies in the (a) first quadrant (b) second quadrant (c) third quadrant (d) fourth quadrant
View SolutionThe equation of the circle of radius 5 and touching the coordinates axes in third quadrant, is
View SolutionThe equation of the circle of radius 5 and touching the coordinate axes in third quadrant is
View SolutionThe straight line through a fixed point (2,3) intersects the coordinate axes at distinct point P and Q. If O is the origin and the rectangle OPRQ is completed then the locus of R is
View Solution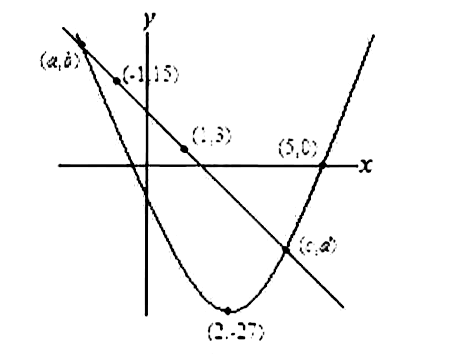
The xy-plane above shows the two points of intersection of the graphs of a linear function and a quadratic function. The leftmost point of intersection has coordinates (a,b) and the rightmost point of intersection has coordinates (c,d) . If the vertex of the graph of the quadratic function is at (2, -27) , what is the value of b−d ?
View SolutionThe locus of the points of trisection of the double ordinates of the parabola y2=4ax is : (A) a straight line (B) a circle (C) a parabola (D) none of these
View SolutionA straight line passes through the points A(-5, 2) and B(3,-6). It intersects the co-ordinate axes at points C and D . Find :
the equation of AB.
View Solution