एक समांतर प्लेट संधारित्र की धारिता का व्यंजक लिखे। दोनों प्लेटों की बीच एक परावैद्युत माध्यम हो, तो संधारित्र की धारिता का व्यंजक व्युत्पन्न करें। इस स्थिति में संचित ऊर्जा का व्यंजक भी निकले।

Video Solution

Text Solution

Verified by Experts

शारिता-किसी चालक के विभव में ईकाई वृद्धि करने के लिए आवश्यक आवेश को र की विद्युत धारिता कहते हैं । दूसरे शब्दों में, धारिता विद्युत् आवेश एवं विभव के अनुपात को कहते हैं।

Sl मात्रक = फेराड $(F) = C V^{- 1}$
समांतर प्लेट संधारितत्र में स्थिर वैद्युत उर्जा-माना कि संधारित्र की धारिता C है तथा उस क्षण उस पर कोई आवेश नहीं है । संधारित्र को बैटरी से जोड़ने पर वह V विभव तक आवेशित होता है । अगर संधारित्र पर q आवेश जमा होता है, तब $q = C V$
यदि संधारित्र में अतिरिक्त आवेश dq स्थानांतरित किया जाता है तो इसके लिए किया गया कार्य संधारित्र विद्युत उर्जा के रूप में संचित रहता है
$d v = d w = V d q = \frac{q}{C} d q$
संधारित्र को $q = 0$ से $q = θ$ तक आवेशन $θ$ तक आवेशन में स्थितिज उर्जा में कुल वृद्धि संधारित्र में कुल संचित उर्जा के बराबर होती है ।
$∴ U = \int d u = \int_{0}^{q} \frac{q}{c} \int_{0}^{q} q d q = \frac{1}{2 c} {[q^{2}]}_{0}^{2} = \frac{1}{2 c} [q^{2} - 0]$
$∴ V = \frac{1}{c} [\frac{θ^{2}}{2}]$
Q=cV
$∴ V = \frac{1}{C} . \frac{C^{2} v^{2}}{2} = \frac{1}{2} c V^{2}, V = \frac{1}{2} c V$
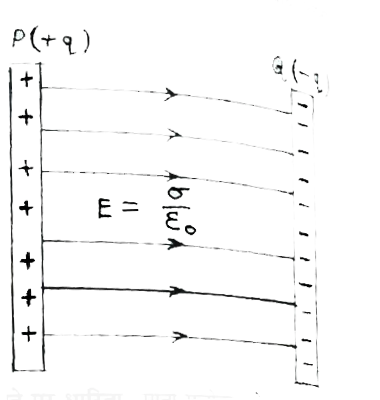
अथवा समान्तर प्लेट वाले संधारित्र की धारिता का व्यंजक-माना कि संधारित्र को दानों व्य दूरी है जैसा कि चित्र में दिखाया गया है । प्लेट P का धनात्मक आवेश (+q) .ऋणात्मक आवेश दिया जाता है । माना कि प्लट P तथा Qका पृष्ठ आवश था $(- q)$ है । प्लेटों के मध्य विद्यत क्षेत्र इस प्रकार व्यक्त किया जाता है ।
$∴ E = \frac{σ}{ε_{0}}$
जहाँ $ε_{0}$ = निरपेक्ष विद्युतशीलता है क्योकि प्लटा के मध्य माध्यम के बीच विभवांतर । है तब V = Ed
$V = \frac{σ}{ε_{0}} d$
$σ = \frac{q}{A} ∴ V = \frac{q}{ε_{0}} \frac{d}{A} ... (i i)$
$C = \frac{q}{V}$
$C = \frac{q ε_{0} A}{q d} = \frac{ε_{0} A}{d}$
$C = \frac{ε_{0} A}{d}$ Ans.

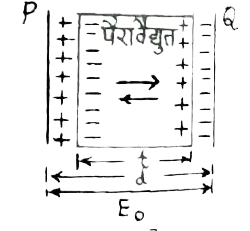
संधारित्र के समान्तर प्लेट के बीच माध्यम रखने पर धारिता-माना प्रत्येक प्ले तथा क्षेत्रफल क्रमश: t तथा A है तथा दोनों प्लेटों के मध्य की दूरी d है। माध्यम पर पर बराबर तथा विपरित आवेश उपस्थित हो जाता है । इन प्रेरित आवेश के कारणरित आवेश के कारण प्रेरित विद्युत क्षेत्र $({\to E}_{p})$ में उत्पन्न हो जाता है जो कि आरोपित क्षेत्र $({\to E}_{0})$ की दिशा के विपरीत दिशा में होता है जैसा कि निम्न चित्र में दिखाया गया है।
निर्वात है । यदि प्लाअत: विद्युत क्षेत्र का पराविद्युत मे समानीत मान $E = E_{0} - E_{p}$
अब .t. मोटाई के पराविद्युत में विद्युत क्षेत्र $E = E_{0} - E_{p}$ तथा $(d - t)$ मोटाई के क्षेत्र में विद्युत क्षेत्र $E_{0}$ है ।
संधारित्र की दोनों प्लेटों के मध्य विभांतर निम्नवत् व्यक्त किया जाता है ।
$V = E_{0} (d - t) + E t$ चूँकि $\frac{E_{0}}{E} = K$ या $E = \frac{E_{0}}{K}$
$∴ V = E_{0} (d - t) + \frac{E_{0}}{K} t$
$V = E_{0} (d - t) \frac{E_{0}}{K} t$
$V = E_{0} [(d - t) + \frac{t}{K}] ... . (i)$
हम जानते हैं $E_{0} = \frac{σ}{ε_{0}} = \frac{q}{ε_{0}}$
:.. समी. () को निम्न प्रकार लिख सकते हैं । $V = \frac{q}{A ε_{0}} [(d - t) + \frac{t}{K}] ... (i i)$
अब संधारित्र की धारिता
$C = \frac{q}{ν} = \frac{q A ε_{0}}{q [(d - t) + \frac{t}{K}]}$
$C = \frac{q ε_{0} A}{(d - t) + \frac{t}{K}}$
$C = \frac{A ε_{0}}{d [(1 - \frac{t}{d}) + \frac{t}{d K}]} ... (i i i)$
कि हम जानते हैं $C_{0} = \frac{ε_{0} A}{d}$
जहाँ $ε_{0}$ प्लेटों के बीच प्लेटों के बीच निर्वात संधारित्र की धारिता ।
(iii) को (iv) से भाग देने पर
$\frac{C}{C_{0}} = \frac{1}{[(1 - \frac{t}{d}) \frac{t}{d K}]} = \frac{1}{[1 - \frac{t}{d} (1 - \frac{1}{K})]}$
$C = \frac{C_{0}}{[1 - \frac{t}{d} (1 - \frac{1}{K})]} ... . (v)$
समी. (v) से स्पष्ट है कि $C > C_{0}$
आत किसी समान्तर प्लेट संधारित्र प्लेटों के मध्य पराविद्युत रखने पर इसी धारिता में वृद्धि हो जाती है।

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

BIHAR BOARD- PREVIOUS YEAR PAPER-प्रश्न पत्र 2010-खण्ड-II (गैर-वस्तुनिष्ठ प्रश्न) दीर्घ उत्तरीय प्रश्न

Home
Ask Doubt
Profile