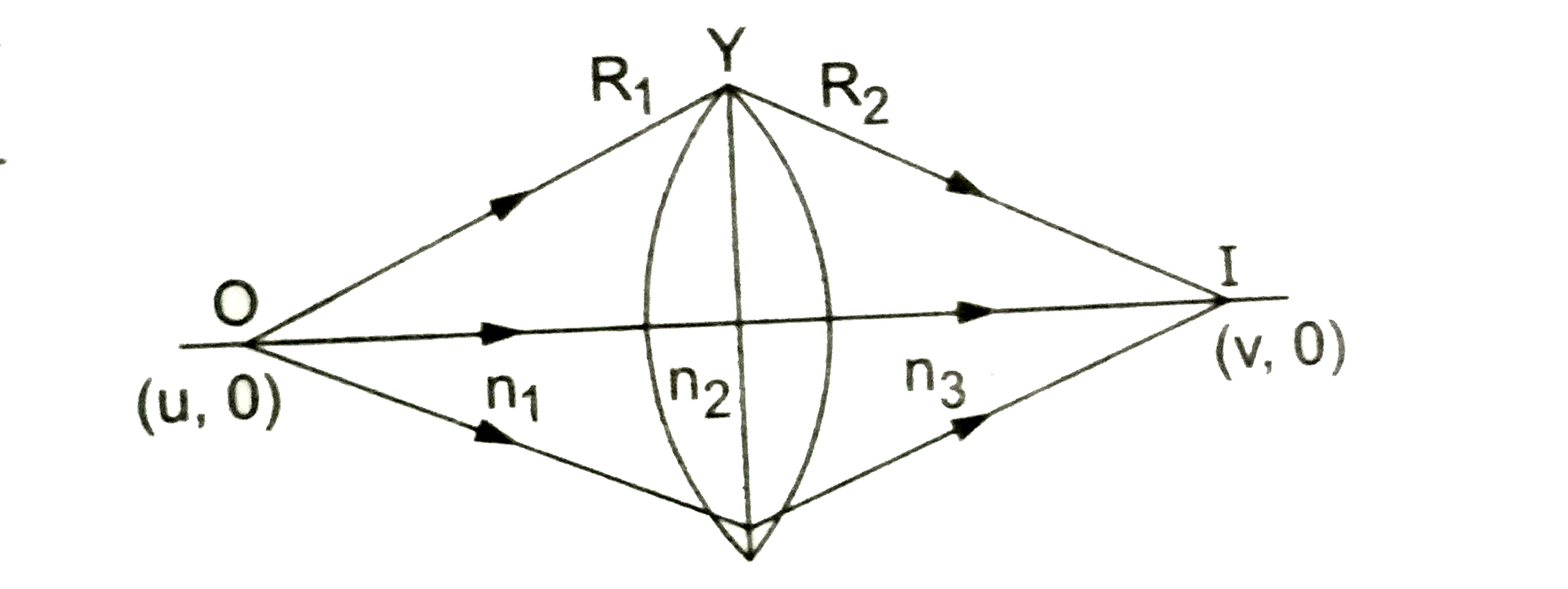
R1 तथा R2 वक्रता -त्रिज्यावाली दो सतहों से घिरे एक लेंस को चित्र के अनुरूप रखा गया है। सिद्ध करें की
n3v−n1u=n2−n1R1+n3−n2R
माना ABC किसी प्रिज्म का मुख्य काट है, जिसका अपवर्तन कोण A है । जैसा कि निम्न चित्र में दर्शाया गया है ।
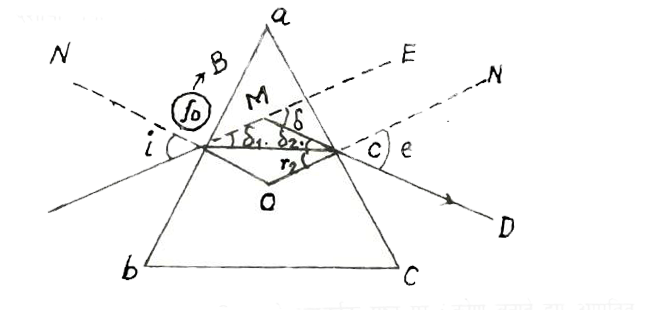
माना एक प्रकाश किरण A B इस प्रिज्म के अपवर्तक पृष्ठ पर । कोण बनाते हुए आपतित लाता है । बिन्दु B पर अपवर्तन के पश्चात् यह प्रकाश किरण अभिलम्ब NO की ओर मुड़ जाती तथा BC के अदिश गति करती है । इस अपवर्तित किरण BC का बिन्दु C पर पुन: आपतन है और यह अभिलम्ब N.0 से दर चली जाती है तथा CD के अनुदिश गति करती है। .करण अभिलम्ब के साथ कोण (∠e) बनाती है । अगर CD को आगे तरफ बढ़ाया जाए सतत किरण को M बिंद पर काटती है। आपतित किरण तथा CD के बीच का कोण δ मान लत हैं, जो कि विचलन कोण कहलाता है । चित्र से स्पष्ट है-∠FRC=∠ABN−∠CBO
δ1=i−r1 तथा δ2=e−r2
:. कुल विचलन कोण, δ=δ1+δ2, या δ=i−r1+e−r2
चतुभुज aBOC से. δ=(i+e)−(r1+r2
∠A+∠aBO+∠BOC+∠OCA=360∘
∠ABO=∠OCa=90∘
∠a+90∘+∠BOC+90∘=360∘
∠A+∠BOC=180∘....(ii)
△BOC से, ∠r1+∠BOLI+∠r2=180∘ समी
(ii) और (iii) से तुलना करने पर,
∠A+∠BOC=∠r1+∠BOC+∠r2
A=r1+r2
समी. (i) और (ii) से, δ=i+e−A
δ+A=i+e
यदि δ=δmi=e ( तथा r1=r2=r (प्रिज्म न्यूनतम विचलन स्थिति
समो. (v) से. δm+A=2iया i=A+δm2....(iv)
समी. (iv))से, 2r=A या r=A/2.....(vii)
स्नेल के नियम से,n=sinisinr
समी. (vi) और (vii)sin(A+δm2)sin(A)2सिद्ध हुआ ।
अथवा, समतुल्य लेंस-यदि दो या दो से अधिक समीक्षीय लेंसों के युग्म के बदले एक ऐसा लेंस लिया जाए, जिसे लेंस युग्म के अक्ष पर उपयुक्त स्थान पर रखने से किसी वस्तु का प्रतिबिम्ब उसी स्थान पर तथा उतने ही आवर्धन का बने, जैसा कि लेंस युक्त द्वारा होता है, तो उस अकेले लेंस को लेंस-युग्म का समतुल्य लेंस कहा जाता है ।
समतुल्य फोकस दूरी का व्यंजक-माना कि दो लेंस L1, तथा _(2) जिनकी फोकस दूरी f1 तथा f2, है एक-दूसरे के साथ स्पर्श करते हुए रखे हुए हैं। माना कि मुख्य अक्ष पर O एक बिन्दु रखा हआ है।
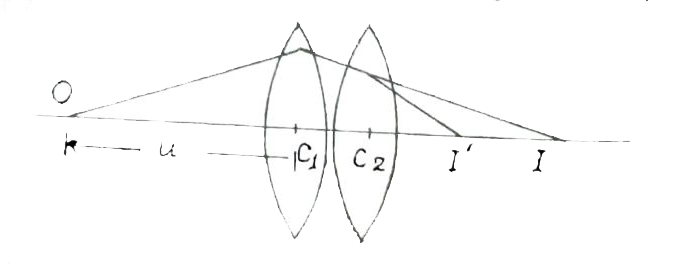
इस बिन्दु बिंब का दो पदों में प्रतिबिंब | बनता है ।
प्रथम पद-इस पद में L1 बिंदु बिंब का प्रतिबिम्ब I बनता है ।
यदि C1O=u तथा C1I=ν
1u+1ν=(10f1
दसरा पद-इस पद में C2 प्रतिबिम्बl l बनाता है जो काल्पनिक है । चौक दानों लंस पतले हैं।
C2I=C1I=+V
C2I=V
C2I=V−1V)+(10V=1f
समी. (1) तथा (ii) को जोड़न पर,
−1u+1V−1V+1v=1f1+1f2
−1u+1V=1f2…(iii)
कल लेंस जिसकी फोकस दूरी f fहो O बिंदु का प्रतिबिंब I बनाए, तो
_1u+1f=1f
समी. (iii) एवं (iv) से,
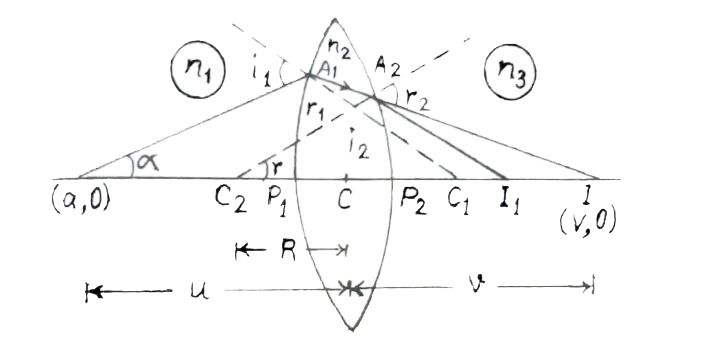
उपरोक्त चित्र से माना सतह X PY के द्वारा बिंदु 0 का प्रतिबिंब I बनाता है
n1P1O+n2P1I=n2−n1P1C1
अब P1O≈CO,PL≈Cl तथा P1C1=CC1 (चूँकि लेंस पतला है)
अतः समी. (i) इस प्रकार लिखा जा सकता है ।
n1CO+n2CI=n2−n1CC1.....(ii)
माना कि अब अपवर्तन XPY से हो रहा है तथा बिन्दु 1, पर वास्तविक प्रतिबिंब बना अतः−n2P1I+n3P2I1=μ2−μ3P2C2
.चूँकि लैंस पतला है
अत: P2I≈C1.P2i1≈CI1) तथा P2C2≈CC2
समो. (iii) से,−n2CI+n3CI1=n2−n3CC2....(iv)
सभी. (ii) और (iv) को जोड़ने पर n1Co+n2CI−n2CI+n3CI1=n2−n1CC1+n2−n1CC2
n1CO+n3CI1=n2−n1CC1=n3−n2CC2...(v)∴CO=−u,CI1=+R1,CC2=−R2
∴n3V−n1u=n2−n1R1+n3−n3R2Proved
Topper's Solved these Questions
- BOOK - BIHAR BOARD- PREVIOUS YEAR PAPERCHAPTER - प्रश्न पत्र 2010EXERCISE - खण्ड-II (गैर-वस्तुनिष्ठ प्रश्न) लघु उत्तरीय प्रश्न11videos
प्रश्न पत्र 2010
- BOOK - BIHAR BOARD- PREVIOUS YEAR PAPERCHAPTER - प्रश्न पत्र - 2016EXERCISE - खण्ड - II : गैर - वस्तुनिष्ठ प्रश्न (दीर्घ उत्तरीय प्रश्न )8videos
प्रश्न पत्र - 2016
- BOOK - BIHAR BOARD- PREVIOUS YEAR PAPERCHAPTER - प्रश्न पत्र 2022EXERCISE - QUESTION96videos
प्रश्न पत्र 2022
Similar Questions
कूलॉम के नियम की सीमाएँ क्या हैं ?
अथवा, विद्युतीय क्षेत्र के लिए अध्यारोपण सिद्धान्त को लिखें और समझाइए।06:15View Solutionयोगिक परावैद्युत वाले एक समांतर प्लेट संधारित्र की धारिता के ले एक व्यंजक प्राप्त करे।
04:06View Solutionनिम्नलिखित में कौन विद्युत चुंबकीय तरंग नहीं है ?
02:57View SolutionLet n1<n2<n3<n4<n5 be positive integers such that n1+n2+n3+n4+n5=20. then the number of distinct arrangements n1,n2,n3,n4,n5 is
02:43View SolutionIf 3*n_(1)-n_(2)P_(2)=^(n_(1)+n_(2))P_(2)=90 then the ordered pair (n_(1),n_(2)) is
View SolutionTwo planets revolve round the sun with frequencies N_(1) and N_(2) revolutions per year. If their average orbital radii be R_(1) and R_(2) respectively, then R_(1)//R_(2) is equal to
01:47View SolutionIf n1+n2=4andn22−n21=8, then calculate maximum value of wavelength emitted in transition form n2→n1forLi2+in nm[GivenRH=107m−1].
02:28View SolutionA biconvex lens made of material with refractive index n2. The radii of curvatures of its left surface and right surface are R1 and R2. The media on its left and right have refreactive indices n1 and n3 respectively. The first and second focal lengths of the lens are respectively f1 and f2.
Assume that R1=R2,n1≠n3. The ratio, f1/f2, of the two focal lengths is equal to06:08View SolutionFor the Paschen series thr values of n_(1) and n_(2) in the expression Delta E = R_(H)c [(1)/(n_(1)^(2))-(1)/(n_(2)^(2))] are
02:38View SolutionA=⎡⎢⎣l1m1n1l2m2n2l3m3n3⎤⎥⎦ and B=⎡⎢⎣p1q1r1p2q2r2p3q3r3⎤⎥⎦
Where pi,qi,ri are the co-factors of the elements li,mi,ni for i=1,2,3. If (l1,m1,n1),(l2,m2,n2) and (l3,m3,n3) are the direction cosines of three mutually perpendicular lines then (p1,q1,r1),(p2,q2,r2) and (p3,q,r3) are01:41View SolutionR1 तथा R2 वक्रता -त्रिज्यावाली दो सतहों से घिरे एक लेंस को चित्र के अनुरूप रखा गया है। सिद्ध करें की
n3v−n1u=n2−n1R1+n3−n2R
 View Solution
View SolutionA=⎡⎢⎣l1m1n1l2m2n2l3m3n3⎤⎥⎦ and B=⎡⎢⎣p1q1r1p2q2r2p3q3r3⎤⎥⎦
Where pi,qi,ri are the co-factors of the elements li,mi,ni for i=1,2,3. If (l1,m1,n1),(l2,m2,n2) and (l3,m3,n3) are the direction cosines of three mutually perpendicular lines then (p1,q1,r1),(p2,q2,r2) and (p3,q,r3) are05:46View SolutionThere are two long co-axial solenoids of same length l. The inner and other coils have redii r1 and r2 and number of turns per unti length n1 and n2 respectively .The reatio of mutual inductance to the self - inductance of the inner- coil is : (A) n1n2 (B) n2n1.r1r2 (C) n2n1.r22r21 (D) n2n1
03:04View SolutionFor the Paschen series the values of n_(1) and n_(2) in the expression DeltaE=R_(H).c(1/(n_(1)^(2))-1/(n_(2)^(2)))
03:20View SolutionTwo planets revolve round the sun with frequencies N1 and N2 revolutions per year. If their average orbital radii be R1 and R2 respectively, then R1/R2 is equal to
02:07View SolutionA=⎡⎢⎣l1m1n1l2m2n2l3m3n3⎤⎥⎦ and B=⎡⎢⎣p1q1r1p2q2r2p3q3r3⎤⎥⎦
Where pi,qi,ri are the co-factors of the elements li,mi,ni for i=1,2,3. If (l1,m1,n1),(l2,m2,n2) and (l3,m3,n3) are the direction cosines of three mutually perpendicular lines then (p1,q1,r1),(p2,q2,r2) and (p3,q,r3) are01:51View Solution

