If equation of path of moving particle is given by $y = 2 x^{2}$ ,radius of curvature of path of particle at origin is

Video Solution

Answer

Step by step video & image solution for If equation of path of moving particle is given by y=2x^(2) ,radius of curvature of path of particle at origin is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Knowledge Check

Question 1 - Select One or More
Initial velocity and acceleration of a particles are as shown in the figure. Acceleration vector of particle remain constant. Then radius of curvature of path of particle $:$

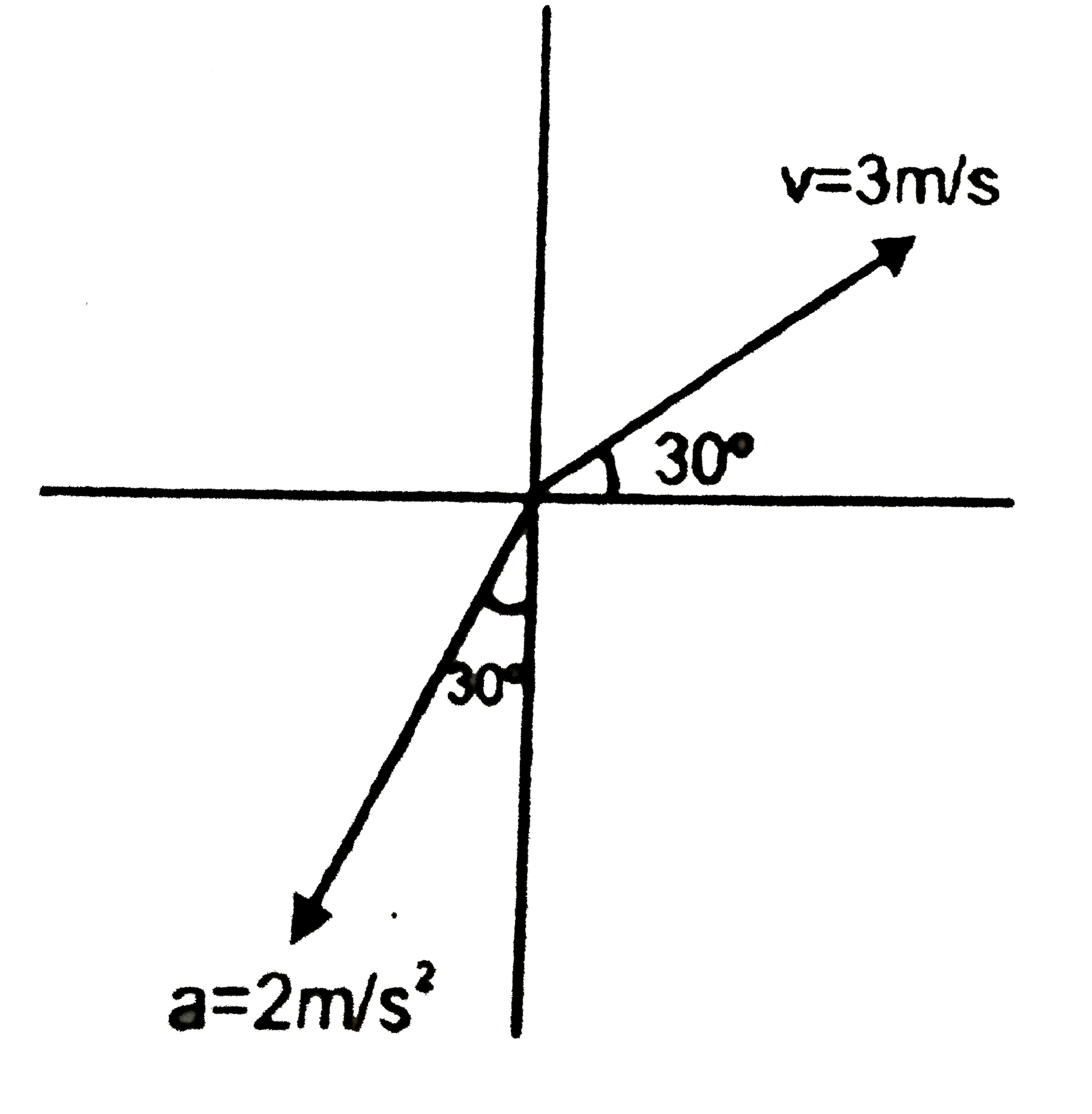Ais $9 m$ initially
Bis $\frac{9}{\sqrt{3}} m$ initially
Cwill have minimum value of $\frac{9}{8} m$
Dwill have minimum value $\frac{3}{8} m$
Question 2 - Select One
Path traced by a moving particle in space is called trajectory of the particle. Shape of trajectiry is decided by the forces acting on the particle. When a coordinate system is associated with a particle motion, the curve equation in which the particle moves $[y = f (x)]$ is called equation of trajectory. It is just giving us the relation among x and y coordinates of the particle i.e. the locus of particle. To find equation of trajectory of a particle, find first x and y coordinates of the particle as a function of time eliminate the time factor.
The position vector of car w.r.t. its starting point is given as $\to r = a t ˆ i - b t^{2} ˆ j$ where a and b are positive constants. The locus of a particle is:-
A $a^{2} y + b x^{2} = 0$
B $a^{2} y = b x^{2}$
C $y = \frac{b}{a^{2}}$
D $a y^{2} = b^{2} x$
Question 3 - Select One
The coordinates of a moving particle at time t are given by $x = c t^{2}$ and $y = b t^{2}$ . The speed of the particle is given by :-
A $2 t (c + b)$
B $2 t \sqrt{c^{2} - b^{2}}$
C $t \sqrt{c^{2} + b^{2}}$
D $2 t \sqrt{c^{2} + b^{2}}$

If equation of path of moving particle is given by $y = 2 x^{2}$ ,radius of curvature of path of particle at origin is

Similar Questions

Knowledge Check

Initial velocity and acceleration of a particles are as shown in the figure. Acceleration vector of particle remain constant. Then radius of curvature of path of particle $:$

The coordinates of a moving particle at time t are given by $x = c t^{2}$ and $y = b t^{2}$ . The speed of the particle is given by :-

Recommended Questions

If equation of path of moving particle is given by y=2x2 ,radius of curvature of path of particle at origin is

Similar Questions

Knowledge Check

Initial velocity and acceleration of a particles are as shown in the figure. Acceleration vector of particle remain constant. Then radius of curvature of path of particle :

The coordinates of a moving particle at time t are given by x=ct2 and y=bt2. The speed of the particle is given by :-

Recommended Questions

If equation of path of moving particle is given by $y = 2 x^{2}$ ,radius of curvature of path of particle at origin is

Initial velocity and acceleration of a particles are as shown in the figure. Acceleration vector of particle remain constant. Then radius of curvature of path of particle $:$

The coordinates of a moving particle at time t are given by $x = c t^{2}$ and $y = b t^{2}$ . The speed of the particle is given by :-