Current flows through a straight, thin-walled tube of radius r. The magnetic field at a distance x from the axis of the tube has magnitude B.
B∝x, for 0 lt x lt r
B∝1/x , for 0 lt x lt r
B=0 , for 0≤x<r
B=0 , only for x=0
The correct Answer is:C
To solve the problem of finding the magnetic field B at a distance x from the axis of a straight, thin-walled tube carrying current I, we can apply Ampere's Circuital Law. Here’s a step-by-step solution:
Step 1: Understanding the Setup
We have a thin-walled tube of radius r carrying a current I. We want to find the magnetic field B at a distance x from the axis of the tube.
Step 2: Applying Ampere's Circuital Law
According to Ampere's Circuital Law, the line integral of the magnetic field B around a closed loop is equal to the permeability of free space μ0 times the total current I enclosed by that loop.
∮B⋅dl=μ0Ienc
Step 3: Analyzing Different Regions
We need to consider different regions based on the value of x:
1. For x<r:
- In this region, there is no current enclosed by the Amperian loop since the current is only flowing through the tube. Therefore, the magnetic field B is zero.
B=0for x<r
2. For x=r:
- At this point, we can use the formula derived from Ampere's Law:
B=μ0I2πr
3. For x>r:
- In this case, the Amperian loop encloses the entire current I. Thus, the magnetic field can be calculated as:
B=μ0I2πx
Step 4: Summarizing the Results
- For 0<x<r: B=0
- For x=r: B=μ0I2πr
- For x>r: B=μ0I2πx
Conclusion
The magnetic field B is zero for distances less than the radius of the tube. It is non-zero and inversely proportional to x for distances greater than the radius.
We have a thin-walled tube of radius r carrying a current I. We want to find the magnetic field B at a distance x from the axis of the tube.
According to Ampere's Circuital Law, the line integral of the magnetic field B around a closed loop is equal to the permeability of free space μ0 times the total current I enclosed by that loop.
We need to consider different regions based on the value of x:
- In this region, there is no current enclosed by the Amperian loop since the current is only flowing through the tube. Therefore, the magnetic field B is zero.
B=0for x<r
- At this point, we can use the formula derived from Ampere's Law:
B=μ0I2πr
- In this case, the Amperian loop encloses the entire current I. Thus, the magnetic field can be calculated as:
B=μ0I2πx
- For 0<x<r: B=0
- For x=r: B=μ0I2πr
- For x>r: B=μ0I2πx
The magnetic field B is zero for distances less than the radius of the tube. It is non-zero and inversely proportional to x for distances greater than the radius.
Topper's Solved these Questions
- PHYSICS PART2BOOK - FIITJEECHAPTER - PHYSICS PART2EXERCISE - Section (I) : Subjective
4 Videos
- PHYSICS PART2BOOK - FIITJEECHAPTER - PHYSICS PART2EXERCISE - Section (II) : MCQ
27 Videos
- PHYSICS PART-IIIBOOK - FIITJEECHAPTER - PHYSICS PART-IIIEXERCISE - NUMERICAL BASED QUESTIONS DECIMAL TYPE
11 Videos
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - COMPREHENSION - IV
2 Videos
Similar Questions
A current l is flowing through a long straight solid conductor of radius R = 4 cm. Magnetic field at a distance 2 cm from the axis of conductor is B0 The distance from the axis, where magnetic field is 1.5 B0 is (current density is uniform)
View SolutionA thin but long, hollow, cylindrical tube of radius r carries a current i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
View Solution
Knowledge Check
Current flows through a straight cylindrical conductor of radius r. The current is distributed uniformly over its cross-section. The magnetic field at a distanace x from the axis of the conductor has magnitude B:
AB=0 at the axisBB∝x for 0≤x≤rCB∝1/x for x>rDB is maximum for x=rA current of 2 amp. flows in a long, straight wire of radius 2mm. The intensity of magnetic field on the axis of the wire is
A(μ0π)×103 TeslaB(μ02π)×103 TeslaC(2μ0π)×103 TeslaDZeroA uniform current is flowing along the length of an infinite, straight, thin, hollow cylinder of radius 'R'. The magnetic field 'B' produced at a perpendicular distance 'd' from the axis of the cylinder is plotted in a graph. Which of the following figure looks like the plot?
A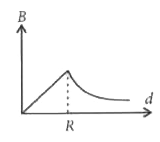 B
B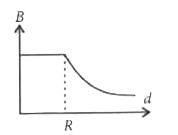 C
C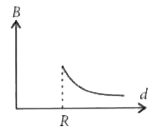 D
D
A current I flows radius along a lengthy thin-walled tube of radisu R with longiitual slit of width h. Find the induction of the magnietic field inside the tube under the condition h<<R
View SolutionA current I flows along a thin-walled, long, half-cylinder of radius R(figure) Find the magnetic induction at a point on the axis of the cylinder
View SolutionA current of I ampere flows along an infinitely long straight thin walled hollow metallic cylinder of radius r. The magnetic field at any point inside the cylinder at a distance x from the axis of the cylinder is
View Solution1A current flows through an infinitely long straight wire. The magnetic field produced at a point 1 metres away from it is
View Solution20 ampere current is flowing in a long straight wire. The intensity of magnetic field at a distance 10 cm from the wire will be
View Solution
