An equilateral triangle of conducting wire of side 'a' is kept in a time (t) varying magnetic field B=B0t, where B0 is constant in such a way that the centre of field coincides with the centroid of the triangle. Now, choose the correct statement.
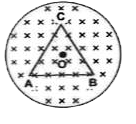
Induced emf in the triangle will be B0a2√3
Induced emf across any side of triangle will be B0a2√3
If a side passes through the centre, the induced emf across that side will remain unchanged
If a side passes through the centre, the induced emf across other sides will increase.
The correct Answer is:D
Topper's Solved these Questions
- PHYSICS PART2BOOK - FIITJEECHAPTER - PHYSICS PART2EXERCISE - Section (I) : Subjective
4 Videos
- PHYSICS PART2BOOK - FIITJEECHAPTER - PHYSICS PART2EXERCISE - Section (II) : MCQ
27 Videos
- PHYSICS PART-IIIBOOK - FIITJEECHAPTER - PHYSICS PART-IIIEXERCISE - NUMERICAL BASED QUESTIONS DECIMAL TYPE
11 Videos
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - COMPREHENSION - IV
2 Videos
Similar Questions
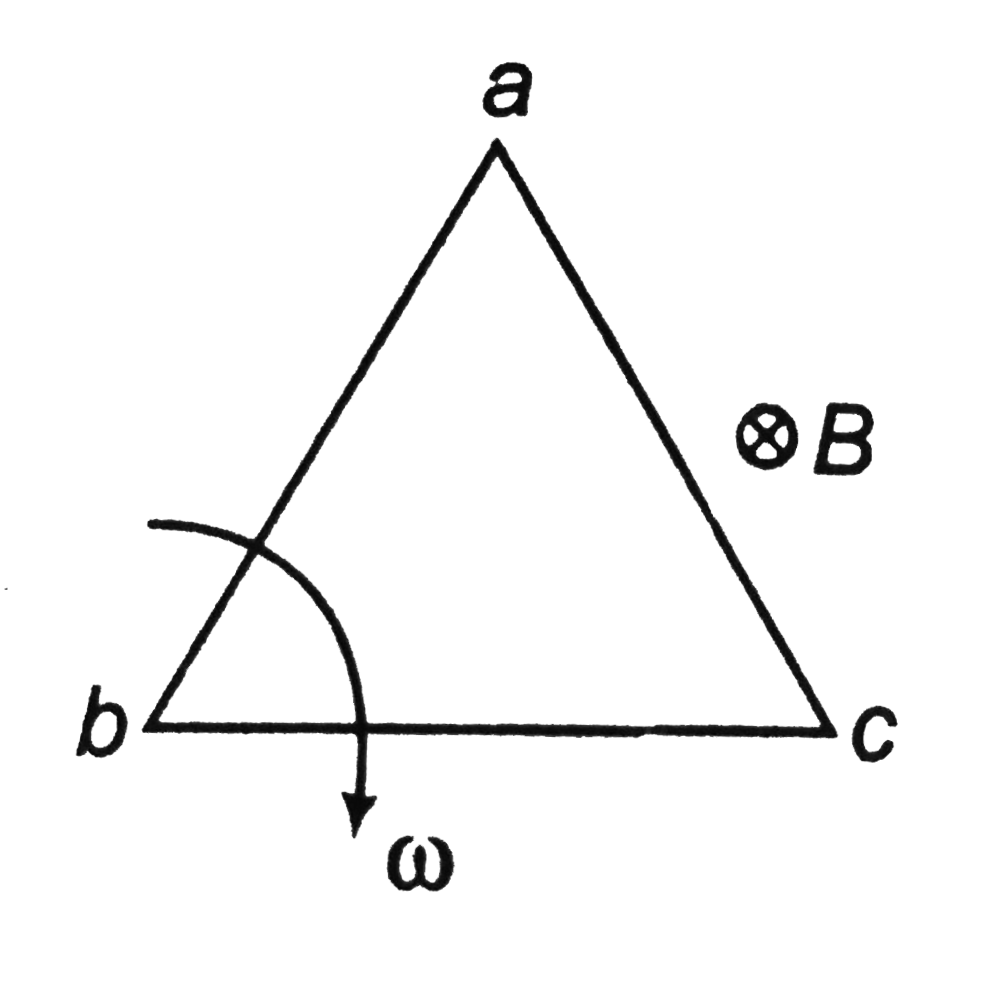
An equilateral triangular conducting frame is rotated with angular velocity ω in a uniform magnetic field B as shown. Side of triangle is l. choose the correct options
View SolutionAn equilateral triangle of side 10cm carries a current of 3A. Find the magnetic field at centroid of triangle.
View Solution
Knowledge Check
A conducting wire of length L is bent in the form of an equilateral triangle. If current I is made to pass through it, then calculate the magnetic field intensity at the centre of the triangle.
A27μ0I4πLB27μ0I2πLC27μ0I5πLD27μ0I7πLAn equilateral triangular conducting frame is rotated with angular velocity ω in a uniform magnetic field B as shown. Side of triangle is l. choose the correct options
 AVa−Vc=0BVa−Vc=Bωl22CVa−Vb=Bωl22DVc−Vb=Bωl22
AVa−Vc=0BVa−Vc=Bωl22CVa−Vb=Bωl22DVc−Vb=Bωl22A triangular wire frame (each side =2m) is placed in a region of time variant magnetic field dB/dt=(√3)T/s. The magnetic field is perpendicular to the plane of the triangle and its centre coincides with the centre of triangle. The base of the triangle AB has a resistance 1(Ω) while the other two sides have resistance 2(Ω) each. The magnitude of potential difference between the points A and B will be
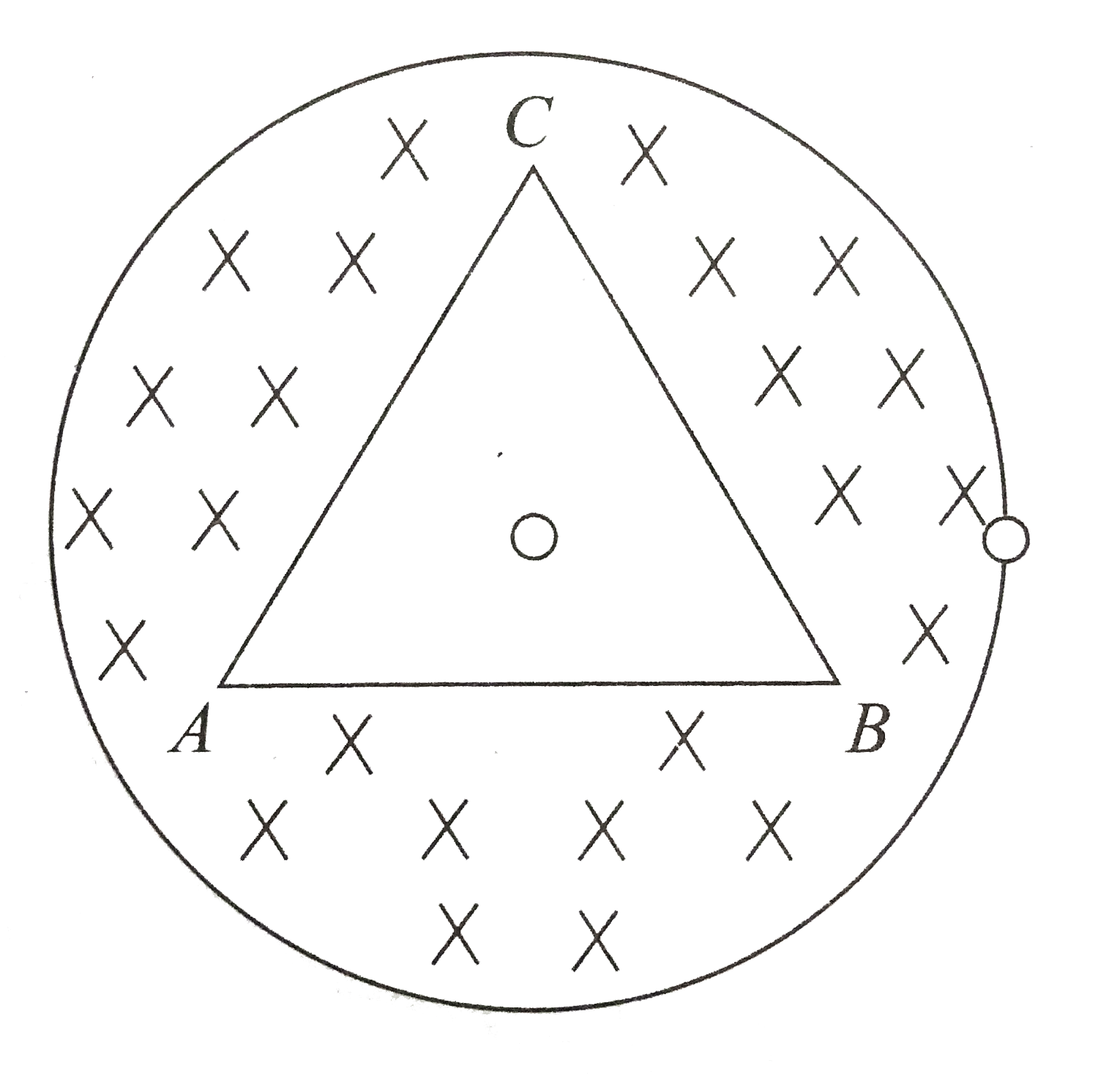 A0.4 VB0.6 VC1.2VDNone
A0.4 VB0.6 VC1.2VDNone
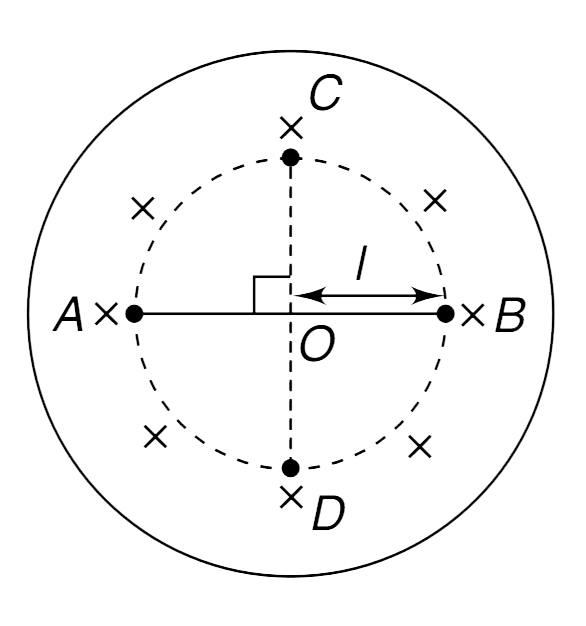
A massless non conducting rod AB of length 2l is placed in uniform time varying magnetic field confined in a cylindrical region of radius (R>l) as shown in the figure. The center of the rod coincides with the centre of the cylin- drical region. The rod can freely rotate in the plane of the Figure about an axis coinciding with the axis of the cylinder. Two particles, each of mass m and charge q are attached to the ends A and B of the rod. The time varying magnetic field in this cylindrical region is given by B=B0[1−t2] where B0 is a constant. The field is switched on at time t=0. Consider B0=100T,l=4cmqm=4π100C/kg. Calculate the time in which the rod will reach position CD shown in the figure for th first time. Will end A be at C or D at this instant ?
View SolutionA triangular wire frame (each side =2m) is placed in a region of time variant magnetic field dB/dt=(√3)T/s. The magnetic field is perpendicular to the plane of the triangle and its centre coincides with the centre of triangle. The base of the triangle AB has a resistance 1(Ω) while the other two sides have resistance 2(Ω) each. The magnitude of potential difference between the points A and B will be

View SolutionA current of 2A is flowing in the sides of an equilateral triangle of side 9 cm. The magnetic field at the centroid of the triangle is
View SolutionA current of 2A is flowing in the sides of an equilateral triangle of side 9 cm. The magnetic field at the centroid of the triangle is
View SolutionA conducting wire of length L is bent in the form of an equilateral triangle. If current I is made to pass through it, then calculate the magnetic field intensity at the centre of the triangle.
View Solution
