One mole of a monoatomic ideal gas undergoes a thermodynamic process such thatV3T2= constant. Then,
work done by the gas is 200R when temperature of the gas is raised by 300 K
the specific heat of the gas in the process is 136R
work done by the gas is 300R when temperature of the gas maised by 600 K
the specific heat of the gas in the process is 214 R
The correct Answer is:A, B
To solve the problem, we need to analyze the thermodynamic process described by the equation V3T2=constant. This indicates that the process is a polytropic process. We will derive the work done by the gas and the specific heat for this process step by step.
1. Identify the relationship:
Given the equation V3T2=C, we can express T in terms of V:
T2=V3C⟹T=√V3C=V3/2√C
2. Using the Ideal Gas Law:
The ideal gas law states that PV=nRT. For one mole of gas (n=1), we have:
PV=RT
Substituting for T from the previous step:
PV=R⋅V3/2√C⟹P=R⋅V1/2√C
3. Finding the Polytropic Index x:
In a polytropic process, PVx=constant. We can express P in terms of V:
P∝V−x⟹R⋅V1/2√C∝V−x
This implies:
V1/2+x=constant
Therefore, we have:
1/2+x=0⟹x=−12
4. Calculating the Work Done:
The work done by the gas in a polytropic process is given by:
W=nRΔT1−x
Here, n=1 (one mole), and substituting x=−12:
W=RΔT1−(−12)=RΔT1+12=RΔT32=2RΔT3
5. Assuming a Change in Temperature:
Let's assume a change in temperature ΔT=300K:
W=2R⋅3003=200R
6. Calculating Specific Heat:
The specific heat C for a polytropic process is given by:
C=Rγ−1+R1−x
For a monoatomic gas, γ=53:
C=R53−1+R1−(−12)=R23+R32=3R2+2R3
Finding a common denominator (6):
C=9R6+4R6=13R6
Final Results:
- The work done by the gas is W=200R.
- The specific heat of the gas during this process is C=13R6.
Given the equation V3T2=C, we can express T in terms of V:
T2=V3C⟹T=√V3C=V3/2√C
The ideal gas law states that PV=nRT. For one mole of gas (n=1), we have:
PV=RT
Substituting for T from the previous step:
PV=R⋅V3/2√C⟹P=R⋅V1/2√C
In a polytropic process, PVx=constant. We can express P in terms of V:
P∝V−x⟹R⋅V1/2√C∝V−x
This implies:
V1/2+x=constant
Therefore, we have:
1/2+x=0⟹x=−12
The work done by the gas in a polytropic process is given by:
W=nRΔT1−x
Here, n=1 (one mole), and substituting x=−12:
W=RΔT1−(−12)=RΔT1+12=RΔT32=2RΔT3
Let's assume a change in temperature ΔT=300K:
W=2R⋅3003=200R
The specific heat C for a polytropic process is given by:
C=Rγ−1+R1−x
For a monoatomic gas, γ=53:
C=R53−1+R1−(−12)=R23+R32=3R2+2R3
Finding a common denominator (6):
C=9R6+4R6=13R6
- The work done by the gas is W=200R.
- The specific heat of the gas during this process is C=13R6.
Topper's Solved these Questions
- PHYSICS PART2BOOK - FIITJEECHAPTER - PHYSICS PART2EXERCISE - Assertion-Reasoning MCQ
12 Videos
- PHYSICS PART2BOOK - FIITJEECHAPTER - PHYSICS PART2EXERCISE - Paragraph Based (MCQ)
3 Videos
- PHYSICS PART2BOOK - FIITJEECHAPTER - PHYSICS PART2EXERCISE - Section (II) : MCQ
27 Videos
- PHYSICS PART-IIIBOOK - FIITJEECHAPTER - PHYSICS PART-IIIEXERCISE - NUMERICAL BASED QUESTIONS DECIMAL TYPE
11 Videos
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - COMPREHENSION - IV
2 Videos
Similar Questions
Knowledge Check
A certain amount of an ideal monoatomic gas undergoes a thermodynamic process such that VT2= constat where V= volume of gas, T= temperature of gas. Then under process
AWhen heat is supplied to gas its temperature will increaseBthe coefficient of volume extension of gas equals −2TCThe molar heat capacity of gas is 2RDWhen heat is supplied to the gas its temperature decreases.One mole of an ideal monatomic gas undergoes a process described by the equation PV3= constant. The heat capacity of the gas during this process is
A32RB52RC2 RDROne mole of an ideal monatomic gas undergoes a process described by the equation PV3 = constant. The heat capacity of the gas during this process is
A32RB52RC2RDR
One mole of a monatomic ideal gas undergoes a cyclic process as shown in the figure (where V is the volume and T is the temperature). Which of the statements below is (are) true ?
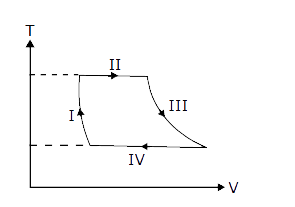
View SolutionOne mole of an ideal monatomic gas undergoes a process described by the equation PV3= constant. The heat capacity of the gas during this process is
View SolutionTwo moles of an ideal mono-atomic gas undergoes a thermodynamic process in which the molar heat capacity 'C' of the gas depends on absolute temperature as C=RTT0, where R is gas consant and T0 is the initial temperature of the gas. (V0 is the initial of the gas). Then answer the following questions:
The equation of process is
View SolutionOne mole of a mono- atomic ideal gas undergoes a quasi- static process, which is depicted by a straight line joining points (V0T0) and (2V0,3T0) in a V - T diagram . What is the value of the heat capacity of the gas at the point (V0,T0) ?
View SolutionOne mole of a monatomic ideal gas undergoes a cyclic process as shown in the figure (where V is the volume and T is the temperature). Which of the statements below is (are) true?
View Solution