A hypothetical planet of mass m is moving along an elliptical path around sun of mass Ms under the influence of its gravitational pull. If the major axis is 2R, find the speed of the planet when it is at a distance of R from the sun.
√GMsR
√2GMsR
2√GMsR
mM√GMsR
The correct Answer is:A
To solve the problem of finding the speed of a hypothetical planet of mass m moving along an elliptical path around the sun of mass Ms when it is at a distance R from the sun, we can follow these steps:
Step 1: Understand the elliptical orbit
The major axis of the elliptical orbit is given as 2R. This means that the semi-major axis a of the ellipse is R.
Step 2: Use Kepler's Third Law
Kepler's Third Law states that the square of the period T of an orbiting body is proportional to the cube of the semi-major axis a:
T2=4π2GMsa3
Substituting a=R:
T2=4π2GMsR3
Taking the square root to find T:
T=2π√R3GMs
Step 3: Determine the speed of the planet
The speed v of the planet at a distance R can be calculated using the formula for the orbital speed:
v=2πrT
where r is the distance from the sun, which is R in this case.
Substituting T from Step 2 into the speed formula:
v=2πR2π√R3GMs
This simplifies to:
v=R√R3GMs
v=R√GMsR3/2=√GMsR
Final Result
Thus, the speed of the planet when it is at a distance R from the sun is:
v=√GMsR
The major axis of the elliptical orbit is given as 2R. This means that the semi-major axis a of the ellipse is R.
Kepler's Third Law states that the square of the period T of an orbiting body is proportional to the cube of the semi-major axis a:
T2=4π2GMsa3
Substituting a=R:
T2=4π2GMsR3
Taking the square root to find T:
T=2π√R3GMs
The speed v of the planet at a distance R can be calculated using the formula for the orbital speed:
v=2πrT
where r is the distance from the sun, which is R in this case.
v=2πR2π√R3GMs
This simplifies to:
v=R√R3GMs
v=R√GMsR3/2=√GMsR
Thus, the speed of the planet when it is at a distance R from the sun is:
v=√GMsR
Topper's Solved these Questions
- PHYSICS PART-IIIBOOK - FIITJEECHAPTER - PHYSICS PART-IIIEXERCISE - ASSIGNMENT SECTION-II SUBJECTIVE
27 Videos
- PHYSICS PART-IIIBOOK - FIITJEECHAPTER - PHYSICS PART-IIIEXERCISE - ASSIGNMENT SECTION-II MCQ (SINGLE CORRECT)
47 Videos
- OPTICSBOOK - FIITJEECHAPTER - OPTICSEXERCISE - NUMERICAL BASED QUESTIONS
2 Videos
- PHYSICS PART2BOOK - FIITJEECHAPTER - PHYSICS PART2EXERCISE - Numerical Based Question Decimal Type
6 Videos
Similar Questions
If a satellite is revolving around a planet of mass M in an elliptical orbit of semi-major axis a. Show that the orbital speed of the satellite when it is at a distance r from the planet will be given by v2=GM[2r−1a]
View SolutionIf a satellite is revolving around a planet of mass Min an elliptical orbit of semi-major axis a. Show that the orbital speed of the satellite when it is at a distance are from the planet will be given by v2=GM[2r−1a]
View Solution
Knowledge Check
A planet of mass m is moving around the sun in an elliptical orbit of semi-major axis a :
AThe total mechanical energy of the planet is varying periodically with timeBThe total energ of the planet is constant and equals −GmMs2a,Ns is mass of sunCTotal mechanical energy of the planet is constant and equals −GmMsa,M2 is mass of sunDDate is insufficient of arrice at a conclusion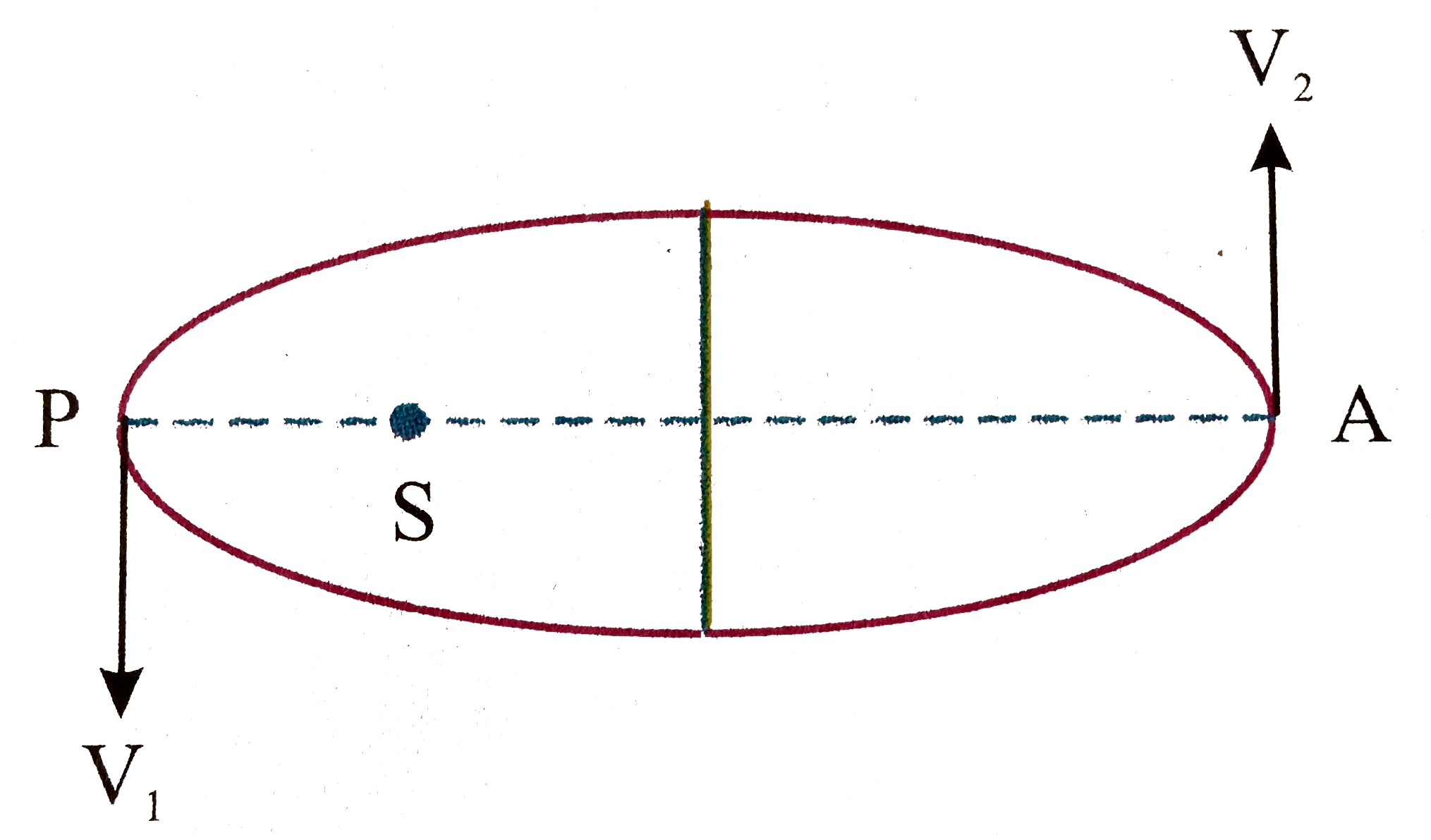
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find speed of planet V2 at aphelion A.A√GMa(1+e)(1−e)B√GMa(1−e)(1+e)C√GMa3(1+e2)(1−e2)D√GMa3(1−e2)(1+e2)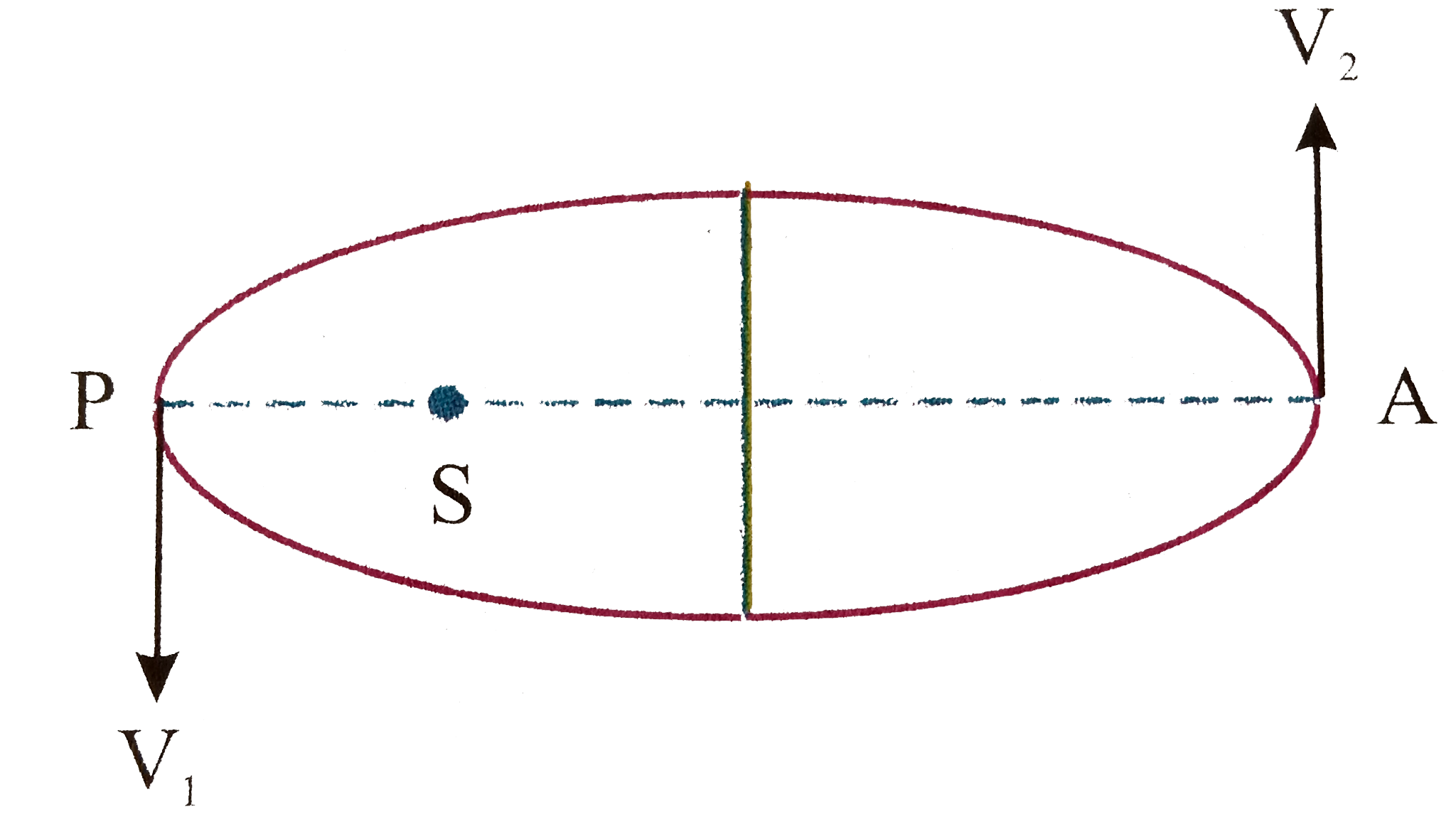
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find speed of planet V1 at perihelion PA√GMa(1+e)(1−e)B1+e1−e√GMaC√GMa3(1+e)(1−e)D√GMa3(1+e2)(1−e2)
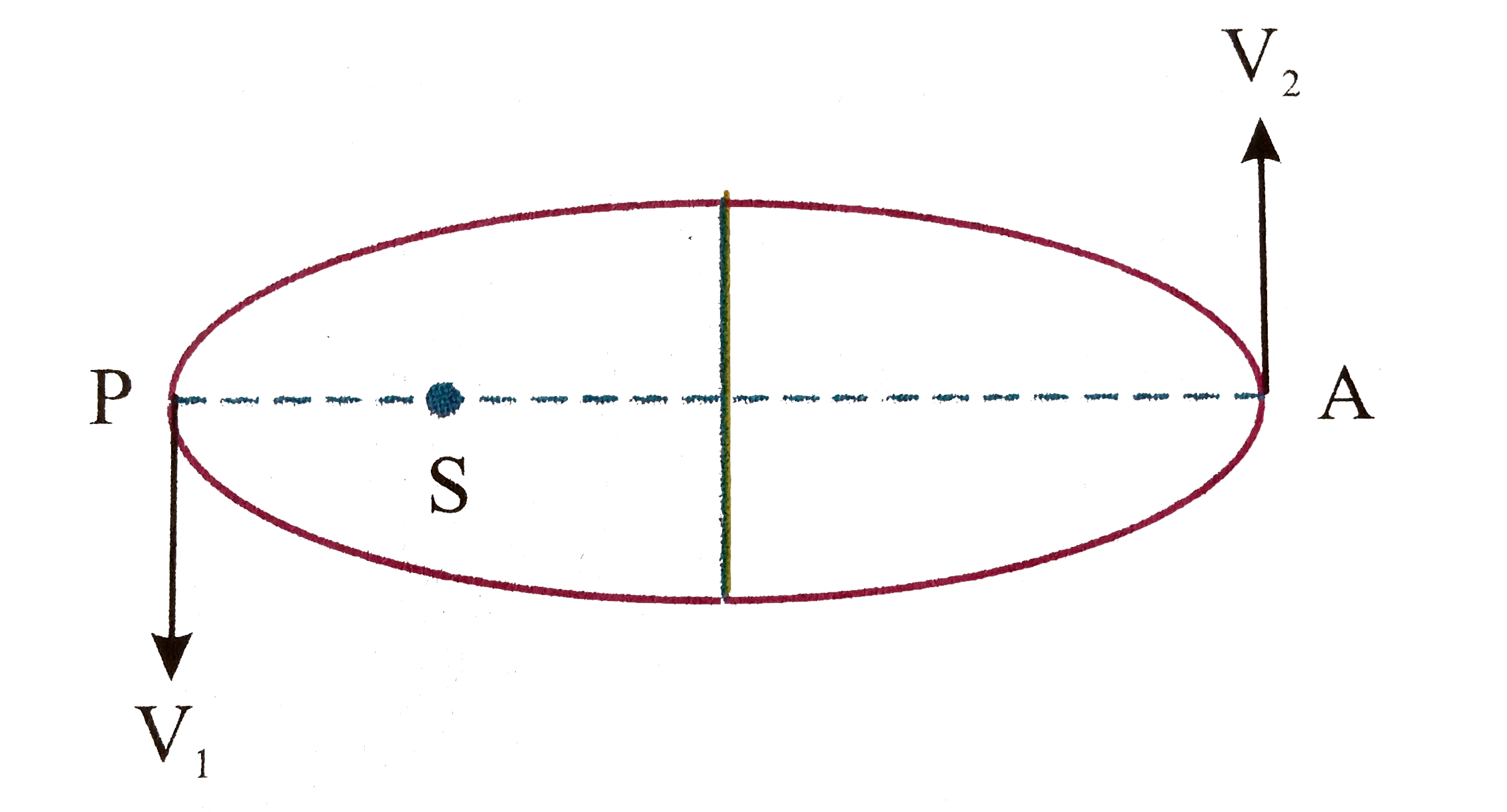
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find total energy of planet interms of given parameters.
View SolutionThe areal velocity of a planet of mass m moving in elliptical orbit around the sun with an angular momentum of L units is equal to
View SolutionThe period of revolution of a planet around the sun is 8 times that of the earth. If the mean distance of that planet from the sun is r, then mean distance of earth from the sun is
View SolutionA planet is revolving in an elliptical orbit around the sun. Its closest distance from the sun is r and the farthest distance is R. If the velocity of the planet nearest to the sun be v and that farthest away from the sun be V. then v/V is
View SolutionTwo point masses M are kept fixed on the x-axis at a distance a from the origin, another point mass m is moving in a circular path of radius R (in y - z plane) under the influence of gravitational force of attraction, then speed of m will be (Assume no forces are acting on m other than the gravitational forces by two M)

View Solution
