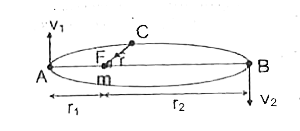
The areal velocity of a planet of mass m moving in elliptical orbit around the sun with an angular momentum of L units is equal to
dAdt=Lm
dAdt=2mL
dAdt=L2m
dAdt=mL
The correct Answer is:C
To solve the problem of finding the areal velocity of a planet of mass m moving in an elliptical orbit around the sun with an angular momentum L, we can follow these steps:
1. Understanding Areal Velocity:
Areal velocity is defined as the rate at which area is swept out by the radius vector of the planet as it moves in its orbit. According to Kepler's second law, this rate is constant for a planet in orbit.
2. Defining Angular Momentum:
The angular momentum L of a planet in orbit can be expressed as:
L=m⋅r⋅v⊥
where r is the distance from the sun to the planet, and v⊥ is the component of the planet's velocity that is perpendicular to the radius vector r.
3. Calculating the Area Swept:
When the planet moves a small distance dA in a time interval dt, the area swept out can be approximated as:
dA=12⋅r⋅v⊥⋅dt
This is the area of the triangle formed by the radius vector and the path of the planet.
4. Finding Areal Velocity:
The areal velocity dAdt is given by:
dAdt=12⋅r⋅v⊥
5. Substituting Angular Momentum:
From the expression for angular momentum, we can express v⊥ in terms of L:
v⊥=Lm⋅r
Substituting this into the areal velocity equation gives:
dAdt=12⋅r⋅(Lm⋅r)
6. Simplifying the Expression:
Simplifying the equation:
dAdt=12⋅Lm
7. Final Result:
Thus, the areal velocity of the planet is:
dAdt=L2m
Conclusion:
The areal velocity of a planet of mass m moving in an elliptical orbit around the sun with an angular momentum of L is given by:
dAdt=L2m
Areal velocity is defined as the rate at which area is swept out by the radius vector of the planet as it moves in its orbit. According to Kepler's second law, this rate is constant for a planet in orbit.
The angular momentum L of a planet in orbit can be expressed as:
L=m⋅r⋅v⊥
where r is the distance from the sun to the planet, and v⊥ is the component of the planet's velocity that is perpendicular to the radius vector r.
When the planet moves a small distance dA in a time interval dt, the area swept out can be approximated as:
dA=12⋅r⋅v⊥⋅dt
This is the area of the triangle formed by the radius vector and the path of the planet.
The areal velocity dAdt is given by:
dAdt=12⋅r⋅v⊥
From the expression for angular momentum, we can express v⊥ in terms of L:
v⊥=Lm⋅r
Substituting this into the areal velocity equation gives:
dAdt=12⋅r⋅(Lm⋅r)
Simplifying the equation:
dAdt=12⋅Lm
Thus, the areal velocity of the planet is:
dAdt=L2m
The areal velocity of a planet of mass m moving in an elliptical orbit around the sun with an angular momentum of L is given by:
dAdt=L2m
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
Knowledge Check
If 'A' is areal velocity of a planet of mass M, its angular momentum is
AM/AB2MACA2MDAM2All the planets move around the sun in
Acircular pathBrectangular pathCelongated elliptical pathDnone of the above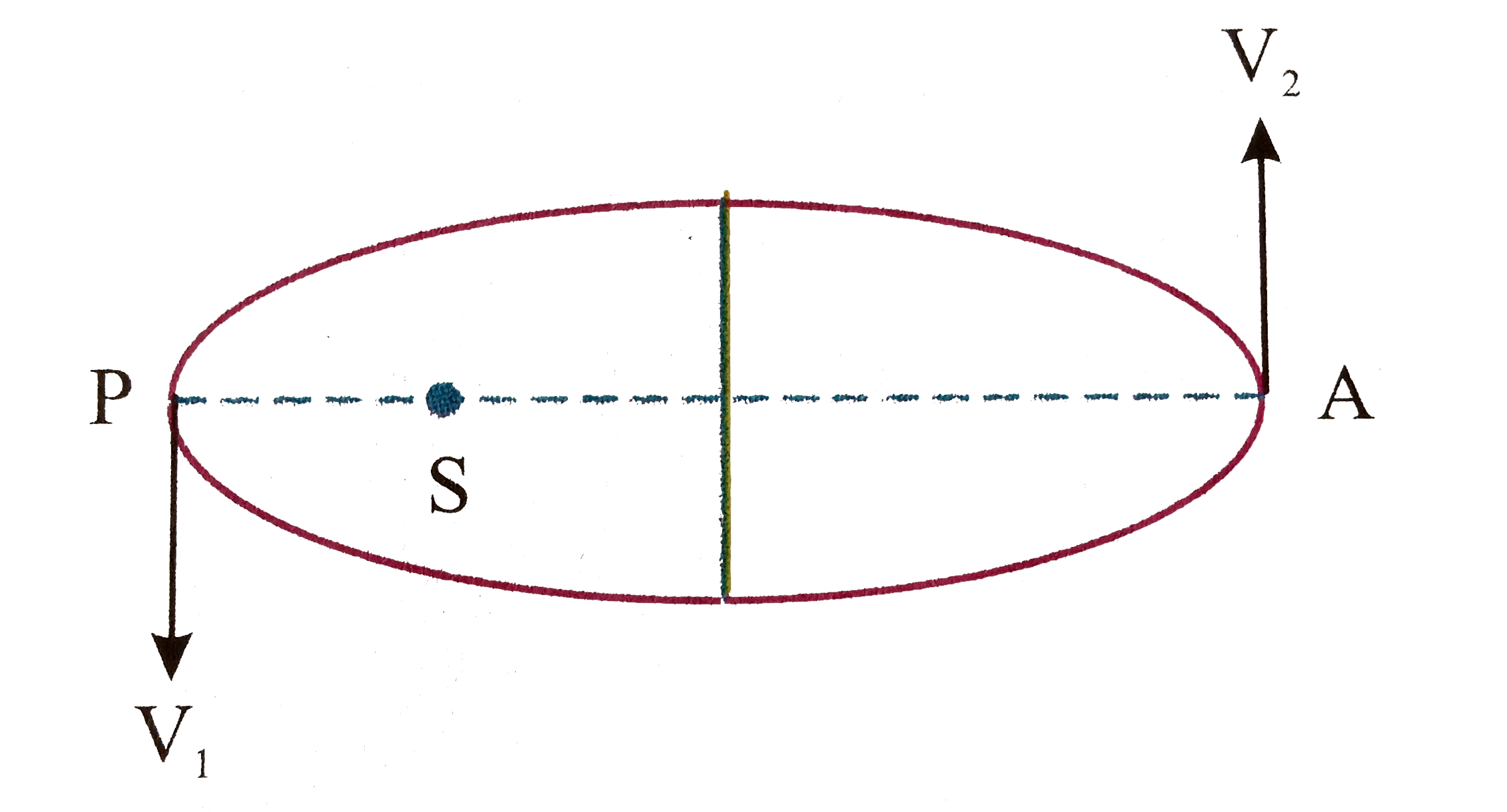
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find total energy of planet interms of given parameters.A−GMm4aB−GMm22aC−GMm8aD−GMm2a
If the angular momentum of a planet of mass m, moving around the Sun in a circular orbit is L, about the center of the Sun, its areal velocity is :
View SolutionThe angular momentum of a planet of mass M moving around the sun in an elliptical orbitis →L. The magnitude of the areal velocity of the planet is :
View SolutionA planet of mass m revolves in elliptical orbit around the sun of mass M so that its maximum and minimum distance from the sun equal to ra and rp respectively. Find the angular momentum of this planet relative to the sun.
View Solution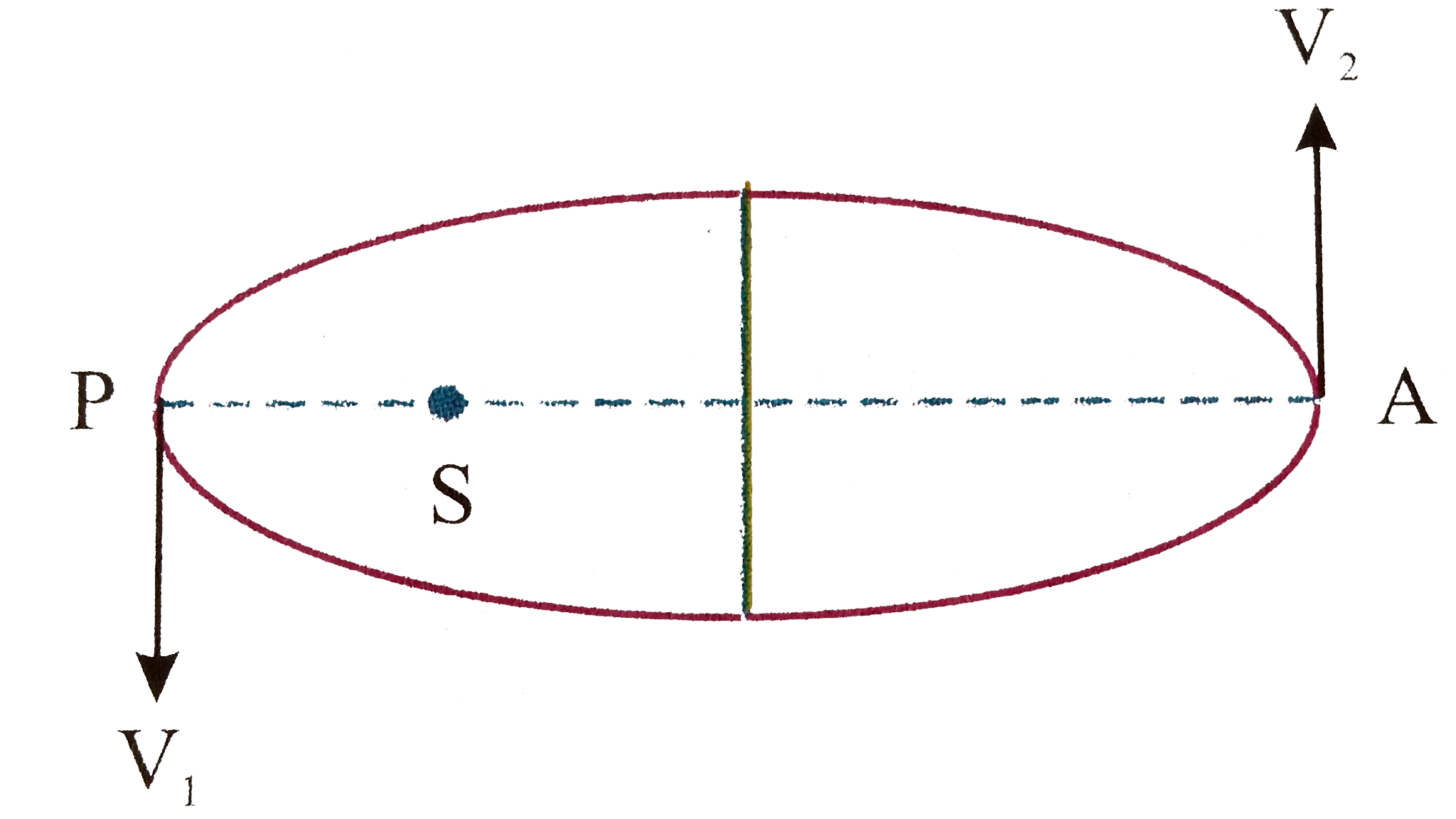
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find speed of planet V1 at perihelion P
View Solution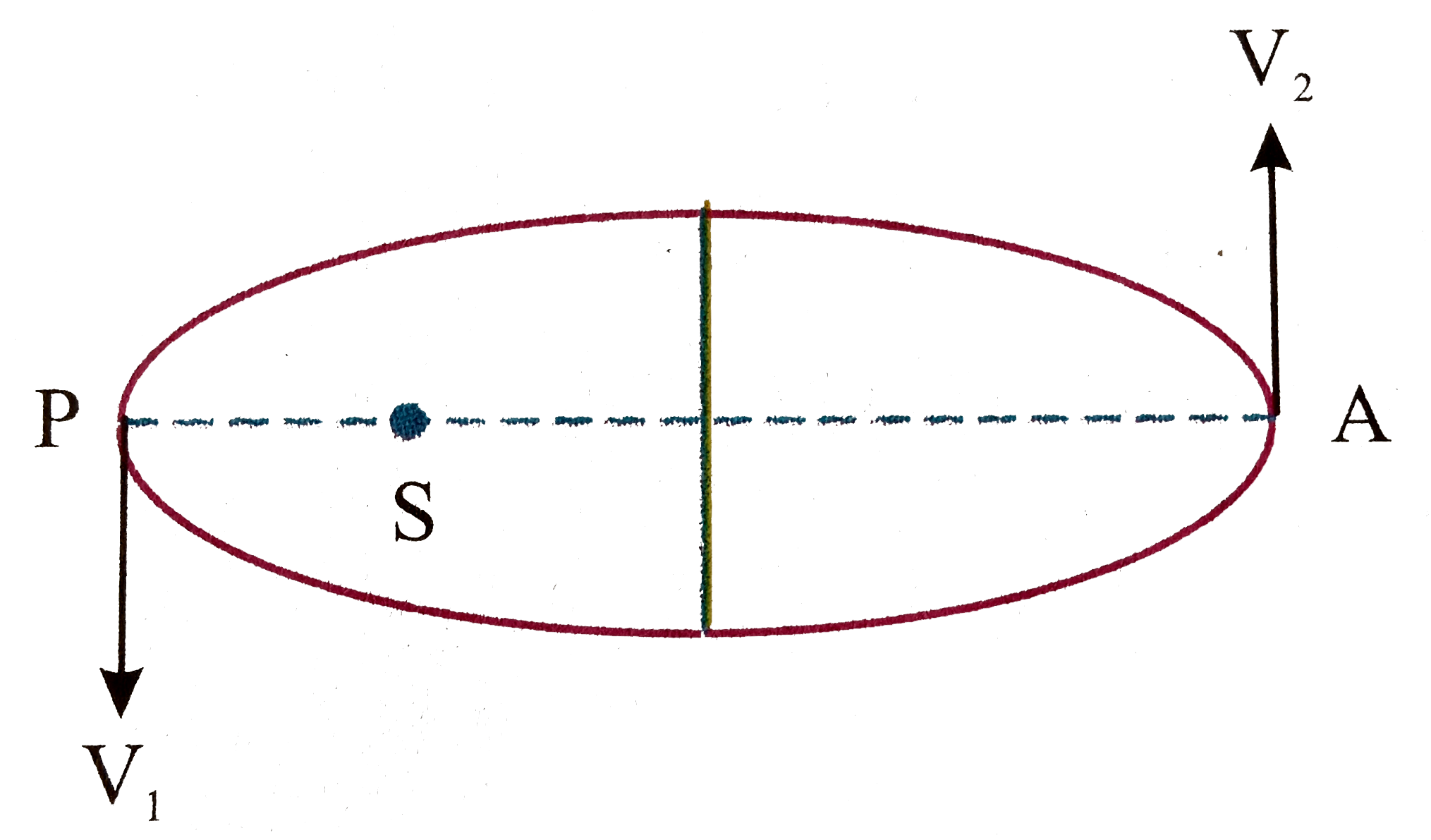
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find speed of planet V2 at aphelion A.
View Solution