A boy of mass m is standing at one end of a boat of mass M and length l. The boy walks to the other end, the displacement of the
CM is zero
boat is mlM+m
boy is mlM+m
boat is mMl
The correct Answer is:B
To solve the problem of the boy walking from one end of the boat to the other, we will analyze the system using the concept of the center of mass.
1. Understanding the System:
- We have a boy of mass m standing at one end of a boat of mass M and length L.
- The boy walks to the other end of the boat.
2. Initial Position of the Center of Mass:
- Let’s denote the initial position of the boy as x1=0 (one end of the boat).
- The center of mass of the boat is at x2=L2 (the midpoint of the boat).
- The total mass of the system is M+m.
3. Calculating Initial Center of Mass:
xcm,initial=m⋅x1+M⋅x2m+M=m⋅0+M⋅L2m+M=M⋅L2m+M
4. Final Position of the Boy and Boat:
- When the boy walks to the other end, his new position is x′1=L.
- Let’s assume the boat shifts left by a distance z, so the center of mass of the boat shifts to x′2=L2−z.
5. Calculating Final Center of Mass:
xcm,final=m⋅x′1+M⋅x′2m+M=m⋅L+M⋅(L2−z)m+M
6. Setting Initial and Final Center of Mass Equal:
- Since there are no external forces acting on the system, the center of mass remains constant:
xcm,initial=xcm,final
M⋅L2m+M=m⋅L+M⋅(L2−z)m+M
7. Simplifying the Equation:
- Cross-multiplying gives:
M⋅L2=mL+M⋅L2−Mz
- Rearranging leads to:
Mz=mL⟹z=mLM+m
8. Displacement of the Boat:
- The displacement of the boat is z=mLM+m.
9. Displacement of the Boy:
- The boy’s displacement is calculated as:
Displacement of the boy=L−z=L−mLM+m=MLM+m
Final Answers:
- The displacement of the boat is mLM+m.
- The displacement of the boy is MLM+m.
- The center of mass of the system does not shift.
- We have a boy of mass m standing at one end of a boat of mass M and length L.
- The boy walks to the other end of the boat.
- Let’s denote the initial position of the boy as x1=0 (one end of the boat).
- The center of mass of the boat is at x2=L2 (the midpoint of the boat).
- The total mass of the system is M+m.
xcm,initial=m⋅x1+M⋅x2m+M=m⋅0+M⋅L2m+M=M⋅L2m+M
- When the boy walks to the other end, his new position is x′1=L.
- Let’s assume the boat shifts left by a distance z, so the center of mass of the boat shifts to x′2=L2−z.
xcm,final=m⋅x′1+M⋅x′2m+M=m⋅L+M⋅(L2−z)m+M
- Since there are no external forces acting on the system, the center of mass remains constant:
xcm,initial=xcm,final
M⋅L2m+M=m⋅L+M⋅(L2−z)m+M
- Cross-multiplying gives:
M⋅L2=mL+M⋅L2−Mz
- Rearranging leads to:
Mz=mL⟹z=mLM+m
- The displacement of the boat is z=mLM+m.
- The boy’s displacement is calculated as:
Displacement of the boy=L−z=L−mLM+m=MLM+m
- The displacement of the boat is mLM+m.
- The displacement of the boy is MLM+m.
- The center of mass of the system does not shift.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - COLLISION EXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) Level - I (ASSERTION REASONING TYPE)2videos
COLLISION
- BOOK - FIITJEECHAPTER - COLLISION EXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) Level - II20videos
COLLISION
- BOOK - FIITJEECHAPTER - COLLISION EXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - II17videos
COLLISION
- BOOK - FIITJEECHAPTER - AC CIRCUITSEXERCISE - ASSERTION REASONING TYPE1videos
AC CIRCUITS
- BOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - Comprehension -43videos
CURRENT ELECTRICITY
Similar Questions
A man of mass m is standing at one end of a trolley of mass M and length L placed at rest on a smooth horizontal surface. The man starts moving towards the other end and covers distance L, then distance moved by man w.r.t ground is
View SolutionA boy of mass 40kg is standing at one ned of the boat (mass : 80 kg) of length 6m in a river. Now the boy reaches to other end of the boat. Find the distance moved by the boat and the distance travelled by boy as seen from the bank of river.Assume that the system is at rest and no friction between the boat and the water.
View Solution
Knowledge Check
- Question 1 - Select One
A boy of mass 50kg is standing at one end of a boat of length 9m and mass 400kg. He runs to the other end. The distance through which the centre of mass of the boat boy system moves is
A0B1mC2mD3m - Question 2 - Select One
A boy having a mass of 40kg stands at one end A of a boat of length 2m at rest. The boy walks to the other end B of the boat and stops. What is the distance moved by the boat? Friciton exists between the feet of the boy and the surface of the boat. But the friction between the boat and the water surface may be neglected. Mass of the boat is 15kg.
 A(a) 0.49mB(b) 2.46mC(c) 1.46mD(d) 3.2m
A(a) 0.49mB(b) 2.46mC(c) 1.46mD(d) 3.2m - Question 3 - Select One
A block of mass 2m is hanging at the lower and of a ropeof mass m and length the l, the other end being fixed to the ceililng. A pulse of wavelength λ0 is produced at the lower of the rope.
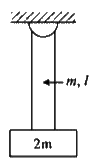
The speed of the pulseat the mid point of rope is:A√52glB√33glC√25glD√gl2
Aboy Walks 4m east and then 3m south .Find the displacement of the boy.
View SolutionA boat of length 10m and mass 450kg is floating without motion in still water. A man of mass 50kg standing at one end of it walks to the other end of it and stops. The magnitude of the displacement of the boat in metres relative to ground is
View SolutionA boy of mass m is standing on a block of mass M kept on a rough surface. When the boy walks from left to right on the block, the centre of mass (boy + block) of the system :
View SolutionA boy of mass m is standing on a block of mass M kept on a rough surface. When the boy walks from left to right on the block, the centre of mass (boy + block) of system :
View SolutionA man of mass M stands at one end of a stationary plank of length L, lying on a smooth surface. The man walks to the other end of the plank. If the mass of the plank is M/3, the distance that the man moves relative to the ground is
View Solution

