A particle of mass m moving at a velocity v strikes with the wall at an angle α with the wall and leaves ball making same angle with the wall. Choose the correct statemet (s) from the following.
The impulsive reaction of wall is 2mV sin α
The impulsive reaction of wall is zero
The coefficient of restitution ≠1
There is no force by particle on the wall
The correct Answer is:A
To solve the problem, we need to analyze the collision of a particle of mass m with a wall at an angle α. The particle strikes the wall with a velocity v and leaves at the same angle α. We will evaluate the four statements provided in the question.
1. Understanding the Collision:
- The particle strikes the wall at an angle α and rebounds off at the same angle.
- The wall is stationary, so its initial velocity is 0.
2. Components of Velocity:
- Before the collision, the velocity of the particle can be resolved into two components:
- Perpendicular to the wall (y-direction): vy=vcosα
- Parallel to the wall (x-direction): vx=vsinα
3. After the Collision:
- After the collision, the particle leaves the wall with the same angle α, so the components of the velocity after collision are:
- Perpendicular to the wall (y-direction): −v′y=−vcosα (the direction is reversed)
- Parallel to the wall (x-direction): v′x=vsinα (the direction remains the same)
4. Change in Momentum:
- The change in momentum along the x-direction (parallel to the wall):
Δpx=m(v′x−vx)=m(vsinα−vsinα)=0
- The change in momentum along the y-direction (perpendicular to the wall):
Δpy=m(−vcosα−mvcosα)=−2mvcosα
5. Impulse on the Wall:
- The impulse imparted by the wall on the particle is equal to the change in momentum:
J=Δpy=−2mvcosα
- The impulse is directed towards the wall, hence the magnitude is 2mvcosα.
6. Coefficient of Restitution:
- The coefficient of restitution e is defined as:
e=Velocity of separationVelocity of approach
- Here, the velocity of separation is vsinα (after collision) and the velocity of approach is vsinα (before collision):
e=vsinαvsinα=1
7. Conclusion:
- Now, let's evaluate the statements:
1. The impulsive reaction of the wall is 2mvsinα: This is incorrect; it should be 2mvcosα.
2. The impulsive reaction of the wall is zero: This is incorrect; there is an impulse.
3. The coefficient of restitution not equals to one: This is incorrect; it equals one.
4. There is no force by the particle on the wall: This is incorrect; there is a force due to the impulse.
Final Answer:
None of the statements are correct.
- The particle strikes the wall at an angle α and rebounds off at the same angle.
- The wall is stationary, so its initial velocity is 0.
- Before the collision, the velocity of the particle can be resolved into two components:
- Perpendicular to the wall (y-direction): vy=vcosα
- Parallel to the wall (x-direction): vx=vsinα
- After the collision, the particle leaves the wall with the same angle α, so the components of the velocity after collision are:
- Perpendicular to the wall (y-direction): −v′y=−vcosα (the direction is reversed)
- Parallel to the wall (x-direction): v′x=vsinα (the direction remains the same)
- The change in momentum along the x-direction (parallel to the wall):
Δpx=m(v′x−vx)=m(vsinα−vsinα)=0
- The change in momentum along the y-direction (perpendicular to the wall):
Δpy=m(−vcosα−mvcosα)=−2mvcosα
- The impulse imparted by the wall on the particle is equal to the change in momentum:
J=Δpy=−2mvcosα
- The impulse is directed towards the wall, hence the magnitude is 2mvcosα.
- The coefficient of restitution e is defined as:
e=Velocity of separationVelocity of approach
- Here, the velocity of separation is vsinα (after collision) and the velocity of approach is vsinα (before collision):
e=vsinαvsinα=1
- Now, let's evaluate the statements:
1. The impulsive reaction of the wall is 2mvsinα: This is incorrect; it should be 2mvcosα.
2. The impulsive reaction of the wall is zero: This is incorrect; there is an impulse.
3. The coefficient of restitution not equals to one: This is incorrect; it equals one.
4. There is no force by the particle on the wall: This is incorrect; there is a force due to the impulse.
None of the statements are correct.
Topper's Solved these Questions
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - (COMPREHENSIONS - I)
2 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - (COMPREHENSIONS - II)
3 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) Level - I (ASSERTION REASONING TYPE)
2 Videos
- AC CIRCUITSBOOK - FIITJEECHAPTER - AC CIRCUITSEXERCISE - ASSERTION REASONING TYPE
1 Videos
- CURRENT ELECTRICITYBOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - Comprehension -4
3 Videos
Similar Questions
A 1kg particle strikes a wall with a velocity 1ms at an angle of 60°with the wall and reflects at the same angle.If it remains in contact with the wall for 0.1sec, then the force is
View SolutionA 1 kg particle strikes a wall with velocity 1 m/s at an angle of 60o with the wall and reflects at the same angle. If it remains in contact with the wall for 0.1 s, then the force is
View Solution
Knowledge Check
A molecule of mass m moving at a velocity v impinges elastically on the wall at an angle a with the wall. Then
Athe impulsive reaction of the wall is 2mvcosαBthe impulsive reaction of the wall is 2mvsinαCthe impulsive reaction of the wall is nonzeroDgiven data is insufficient to calculate impulsive reaction of the wallA 1 kg particle strikes a wall with velocity 1 m/s at an angle of 60∘ with the wall and reflects at the same angle. If it remains in contact with wall for 0.1 s, then the force is
A0B10√3 NC30√3ND40√3NA lead ball strikes a wall and falls down, a tennis ball having the same mass and velocity strikes the wall and bounces back. Check the correct statement
AThe momentum of the lead ball is greater than that of the tennis ballBThe lead ball suffers a greater change in momentum compared with the tennis ballCThe tennis ball suffers a greater change in momentum as compared with the lead ballDBoth suffer an equal change in momentum
A body of mass 3 kg moving with velocity 10 m/s hits a wall at an angle of 60∘ and returns at the same angle. The impact time was 0.2 s. Calculate the force exerted on the wall.
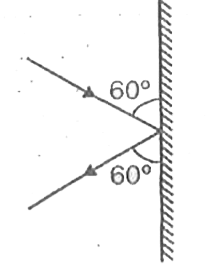
View SolutionA particle of mass m strikes a wall with speed v at an angle 30∘ with the wall elastically as shown in the figure. The magnitude of impulse imparted to the ball by the wall is
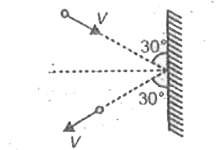
View SolutionA 0.5 kg ball moving with a speed of 12 m/s strikes a hard wall at an angle of 30∘ with the wall. It is reflected with the same speed and at the same angle. If the ball is in contact with the wall for 0.25 s, the average force acting on the wall is :
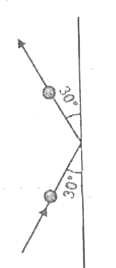
View SolutionA parallel beam of particles of mass m moving with velocity v impinges on a wall at an angle θ to its normal. The number of particles per unit volume in the beam is n. If the collision of particles with the wall is elastic, then the pressure exerted by this beam on the wall is
View SolutionA ball strikes a wall with a velocity →u at an angle θ with the normal to the wall surface. and rebounds from it at an angle β with the surface. Then
View Solution
