For the arrangement shown in figure, the spring is inilially compressed by 3cm. When the spring is released the block collides with the wall and rebounds to compress the spring again.

If the time starts at the instant when spring is released, find the minimum time after which the block becomes stationary.
If collision is elastic then In the case of spring - mass system, since the time period is independent of the amplitude of oscillation therefore.

T=T02π[π+2sin−1(13)]
T=√mk[π+2sin−1(13)]
Case- II if collision is inelastic From t = 0 to before collsion let time is t1
t1=T04+T02πsin−1(13)
After collision the amplitude will changed to √5 therefore if the time is t2 before coming rest instantaneously then
t2=T04+T02πsin−1(1√5)
Total time taken T=t1+t2
T=√mk[π+sin−1(13)+sin−1(1√5)]
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Solved Problems (Subjective)
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Solved Problems (Objective)
16 Videos
- SEMICONDUCTOR AND DEVICEBOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I
20 Videos
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
Similar Questions
For the arrangement shown in figure, the spring is initially compressed by 3cm. When the spring is released the block collides with the wall and rebounds to compress the spring again.

(a) If the coefficient of restitution is 1√2 , find the maximum compression in the spring after collision.
(b) If the time starts at the instant when spring is released, find the minimum time after which the block becomes stationary.
View SolutionFor the arrangement shown in figure, the spring is initially compressed by 3cm. When the spring is released the block collides with the wall and rebounds to compress the spring again.

(a) If the coefficient of restitution is 1√2 , find the maximum compression in the spring after collision.
(b) If the time starts at the instant when spring is released, find the minimum time after which the block becomes stationary.
View Solution
Knowledge Check
The spring is compressed by a distance a and released. The block again comes to rest when the spring is elongated by a distance b. During this
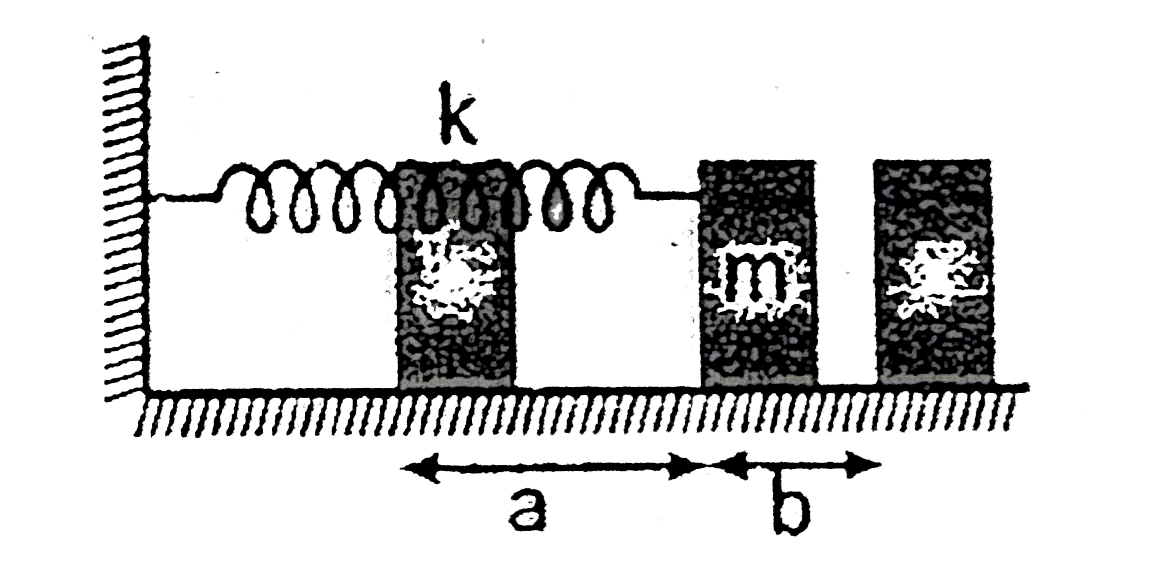 Awork done by sprinn on the block =12k(a+b)2Bwork done by sprinn on the block =12k(a2−b2)Cco-eff. of frication =k(a−b)2mgDco-eff. of frication =k(a+b)2mg
Awork done by sprinn on the block =12k(a+b)2Bwork done by sprinn on the block =12k(a2−b2)Cco-eff. of frication =k(a−b)2mgDco-eff. of frication =k(a+b)2mgFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.
 AmgBmg/2C3mg/2D2 mg
AmgBmg/2C3mg/2D2 mg

In the figure, the spring is initially compressed by 3 cm and released. The block collides withth wall and rebounds to compress the spring again. The maximum compression in the srping after collision (coefficient of restitution is 0.7) is ........cm (Take √5=2.4,k=104Nm−1)
View SolutionA ball is placed on a compressed spring. When the spring is released, the ball is observed to fly away.

What form of energy does the compressed spring possess ?
View SolutionA ball is placed on a compressed spring. When the spring is released, the ball is observed to fly away.

Why does the ball fly away?
View SolutionThe spring is compressed by a distance a and released. The block again comes to rest when the spring is elongated by a distance b. During this
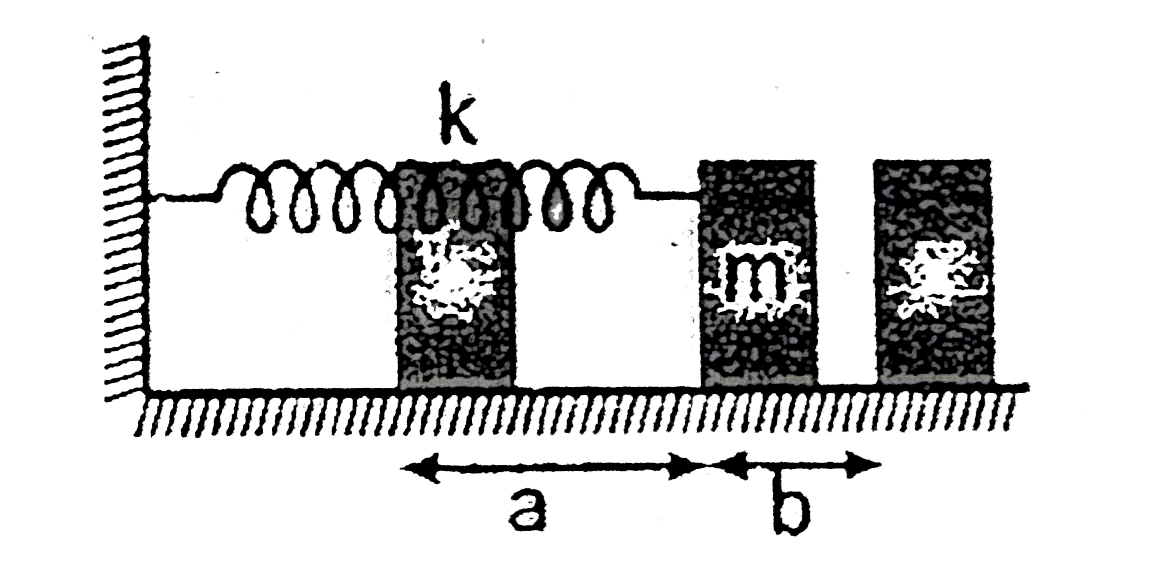
View SolutionFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.

View SolutionThe block shown in figure is released from rest. Find out the speed of the block when the spring is compressed by 1 m

View Solution
