
In the figure, the spring is initially compressed by 3 cm and released. The block collides withth wall and rebounds to compress the spring again. The maximum compression in the srping after collision (coefficient of restitution is 0.7) is ........cm (Take √5=2.4,k=104Nm−1)
The correct Answer is:2.24
From energy conservation
12mv20+12kx2=12kx20
⇒v0=√km(x20−x2)
………[velocity of block just before collision]
Here x0=0.03m,x=0.01m
k=104N/m,m=1kg
v0=√1041[(0.03)2−(0.01)2]
=√104×10−4[9−1]
=2m/s.............[∴Take0.7≈1√2]
maximum compression in the sprnig,
12kx2m=12kx2+12mv2
⇒xm=√x2+mkv2
=√(0.01)2+1(2)2104
=√1+4102=2.24102m
∴xm=2.24cm
Topper's Solved these Questions
Similar Questions
For the arrangement shown in figure, the spring is initially compressed by 3cm. When the spring is released the block collides with the wall and rebounds to compress the spring again.

(a) If the coefficient of restitution is 1√2 , find the maximum compression in the spring after collision.
(b) If the time starts at the instant when spring is released, find the minimum time after which the block becomes stationary.
View SolutionFor the arrangement shown in figure, the spring is initially compressed by 3cm. When the spring is released the block collides with the wall and rebounds to compress the spring again.

(a) If the coefficient of restitution is 1√2 , find the maximum compression in the spring after collision.
(b) If the time starts at the instant when spring is released, find the minimum time after which the block becomes stationary.
View Solution
Knowledge Check
The ball sticks to block C, then block Ccollides elastically , head - on with A. If the maximum compression is x0, the spring constant k is
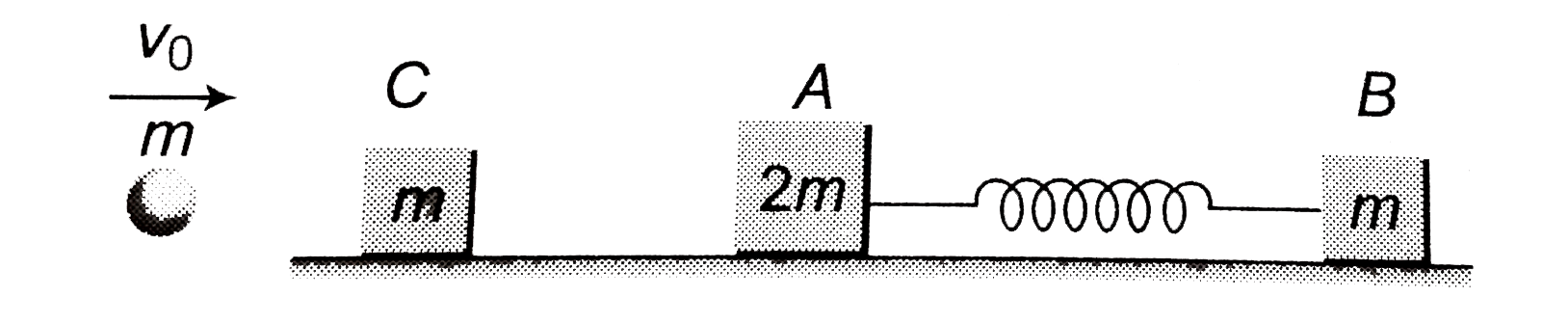 A23mv20x20Bmv202x20Cmv203x20Dmv206x20
A23mv20x20Bmv202x20Cmv203x20Dmv206x20The block of mass M moving on the frictionless horizontal surface collides with the spring constant k and compresses it by length L . The maximum momention of the block after collision is
 AkL22MB√MkL(c)SCML2kDzero
AkL22MB√MkL(c)SCML2kDzeroThe system shown in the figure can move on a smooth surface. The spring is initially compressed by 6 cm and then released.
 Athe particles perform SHM with time period π10secBthe block of mass 3 kg perform SHM with amplitude 4 cmCthe block of mass 6 kg will have maximum momentum 2.40kgm/sDnone of these
Athe particles perform SHM with time period π10secBthe block of mass 3 kg perform SHM with amplitude 4 cmCthe block of mass 6 kg will have maximum momentum 2.40kgm/sDnone of these
For the arrangement shown in figure, the spring is inilially compressed by 3cm. When the spring is released the block collides with the wall and rebounds to compress the spring again.

If the time starts at the instant when spring is released, find the minimum time after which the block becomes stationary.
View SolutionThe block of mass M moving on the frictionless horizontal surface collides with the spring constant k and compresses it by length L . The maximum momention of the block after collision is

View SolutionThe system shown in the figure can move on a smooth surface. The spring is initially compressed by 6 cm and then released.

View SolutionThe system shown in the figure can move on a smooth surface. The spring is initially compressed by 6cm and then released.Find
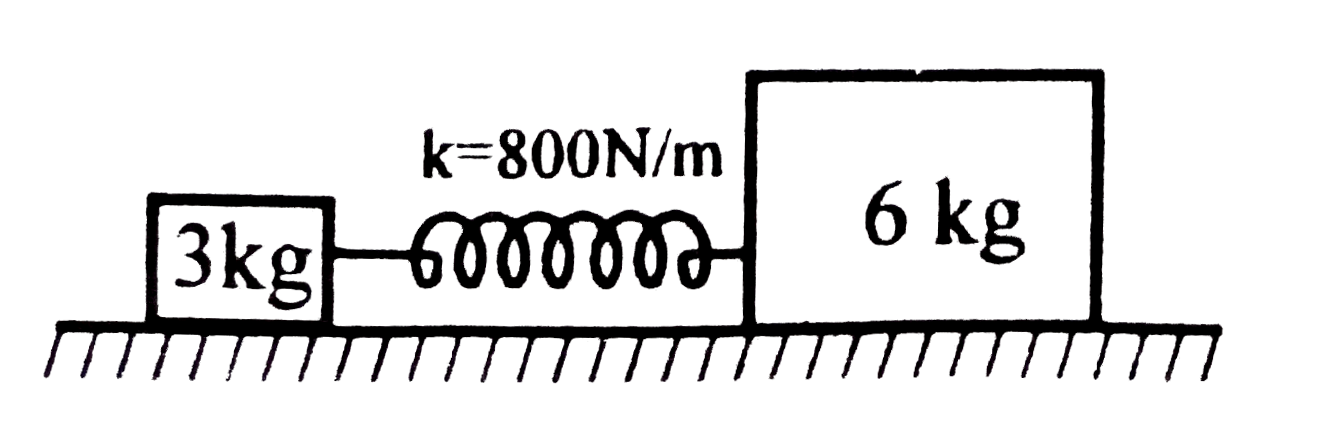
(a) time perod
(b) amplitude of 3kg block
(c ) maximum momentum of 6kg block
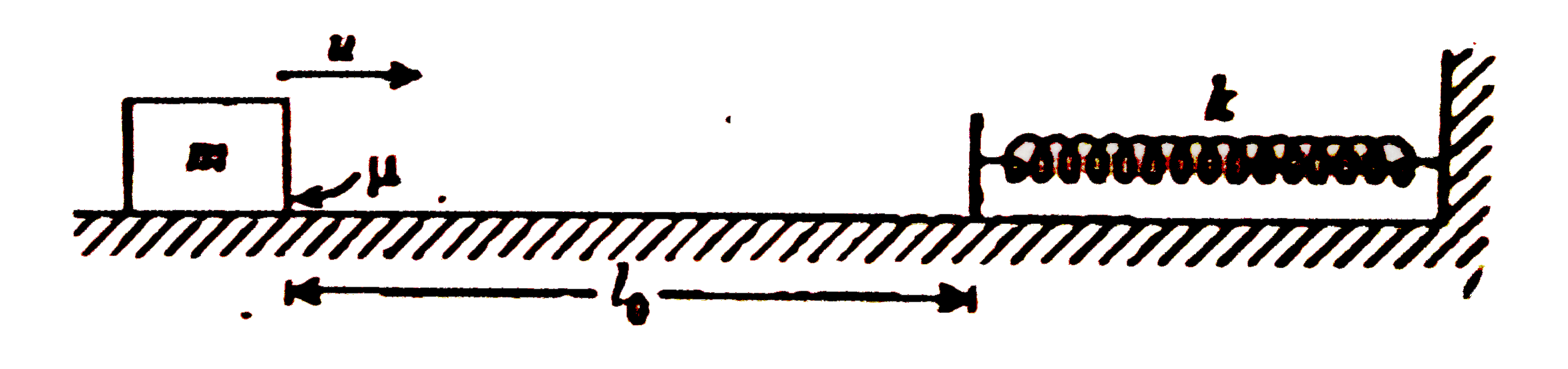
View SolutionFigure. shows a rough horizontal plane which ends in a vertical wall, to which a spring is connected, having a force constant k. Initially spring is in its relaxed state. A block of mass m starts with an initial velocity u towards the spring from a distance l0 from the end of spring shown. When block strikes at the end ofthe spring, it compresses the spring and comes to rest. Find the maximum compression in the spring. The friction coefficient between the block and the floor is μ..
View Solution
