A block of mass m attached with a spring and held by a person such that the spring is in natural length l0. Now the man releases the block, the ratio of maximum compression in the spring in the given situation , to that of the compression at equilibrium position.

2:1
1:1
1:2
√2:1
The correct Answer is:A
The loss of potential energy by the gravity = gain in potential energy in the spring for maximum compression
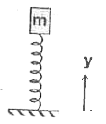
mgx=12kx2⇒x=2mgk
At equilibrium Σfx=0
mg−kx0=0
⇒x0=mgk
So, required ratio =2:1
Hence (A) is correct
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - COMPREHENSION17videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reason type1videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Solved Problems (Subjective)13videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I20videos
SEMICONDUCTOR AND DEVICE
- BOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS747videos
TEST PAPERS
Similar Questions
The ball strikes the block and sticks to it. Find the maximum compression of spring. (L: natural length of spring)
 View Solution
View SolutionA block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
If blocks collide elastically head - on , the ratio of maximum compression of the left spring and the right spring will be
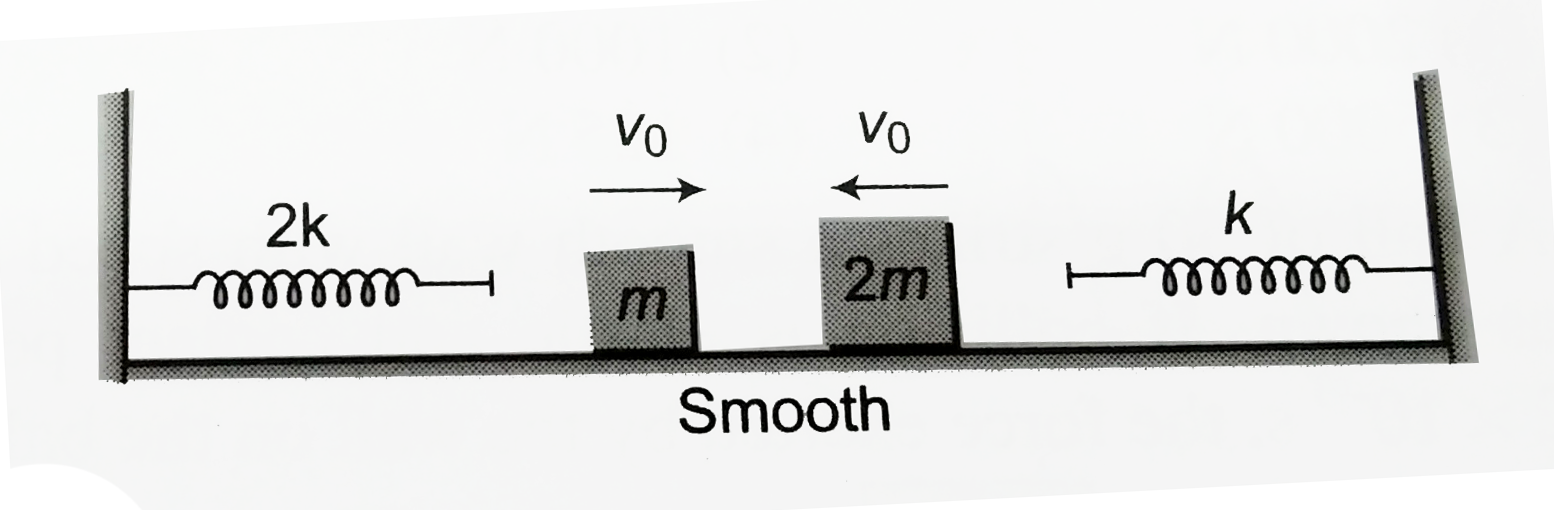 A3:5B2:3C5:4D5:2
A3:5B2:3C5:4D5:2 - Question 2 - Select One
Block A of mass m is placed on a plank B . A light support S is fixed on plank B and is attached with the block A with a spring of spring constant K. Consider that initialy spring is in the natural length, and the system is at rest. Find the maximum compression in the spring, if the plank B is moved with a constant acceleration 'a' . (All the surface are smooth) :
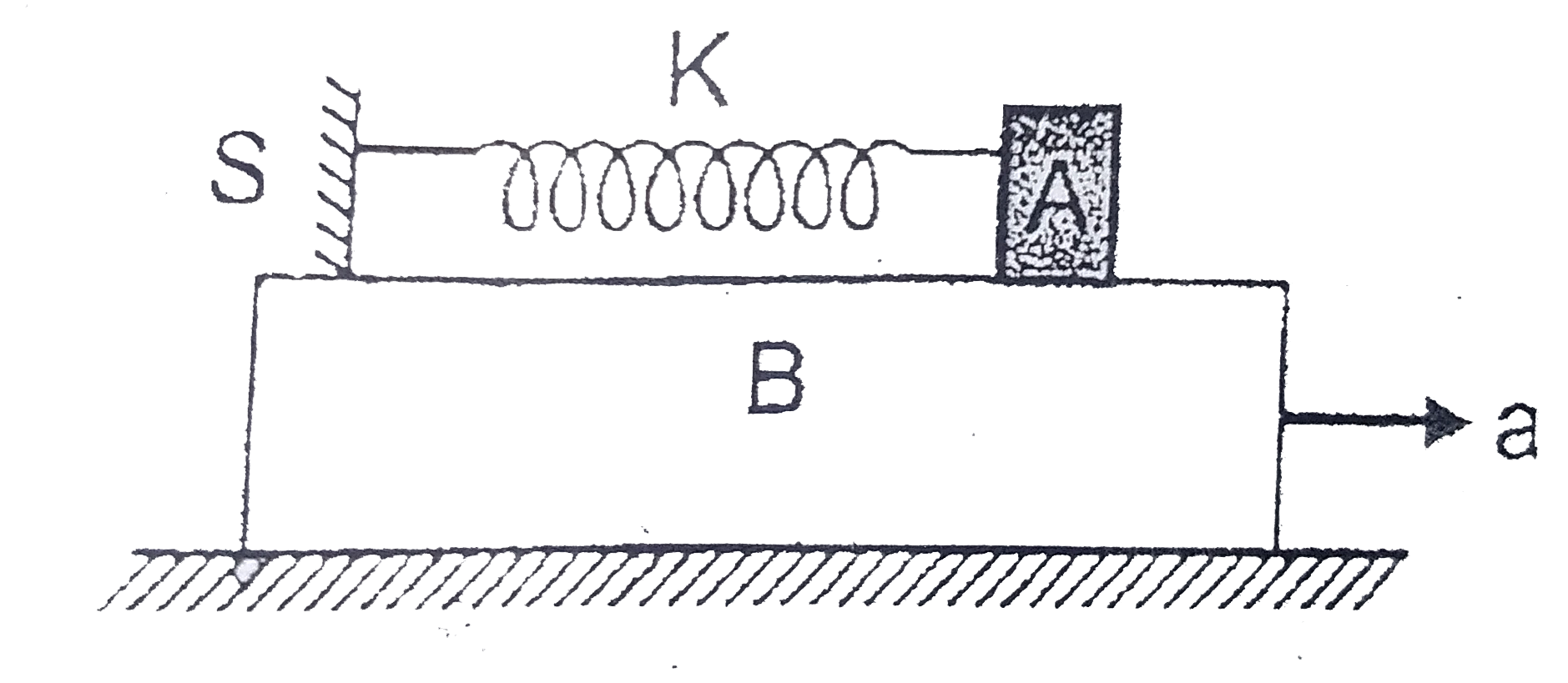 Ama2KB2maKCmaKD2maK
Ama2KB2maKCmaKD2maK - Question 3 - Select One
A block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
 A14√mv2kB√mv2kC12√mv2kD2√mv2k
A14√mv2kB√mv2kC12√mv2kD2√mv2k
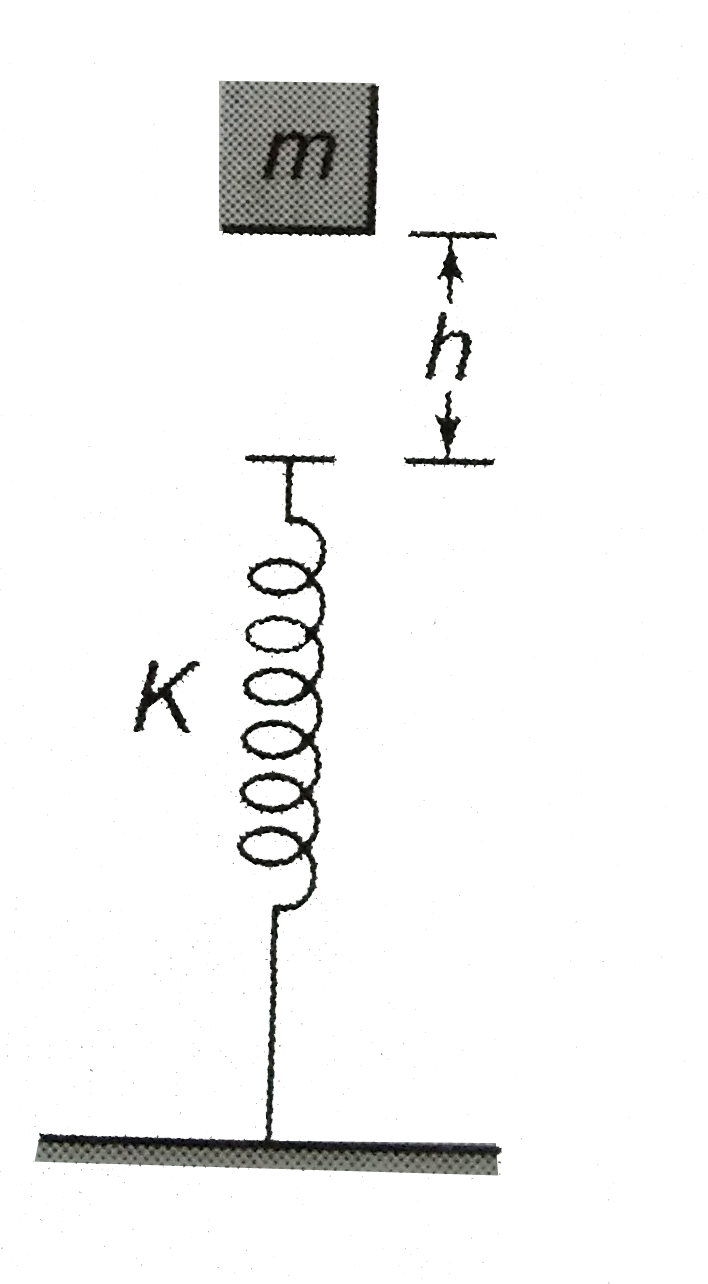
A block is released from height h, find the maximum compression of spring of spring constant k.View SolutionFigure. shows a rough horizontal plane which ends in a vertical wall, to which a spring is connected, having a force constant k. Initially spring is in its relaxed state. A block of mass m starts with an initial velocity u towards the spring from a distance l0 from the end of spring shown. When block strikes at the end ofthe spring, it compresses the spring and comes to rest. Find the maximum compression in the spring. The friction coefficient between the block and the floor is μ..
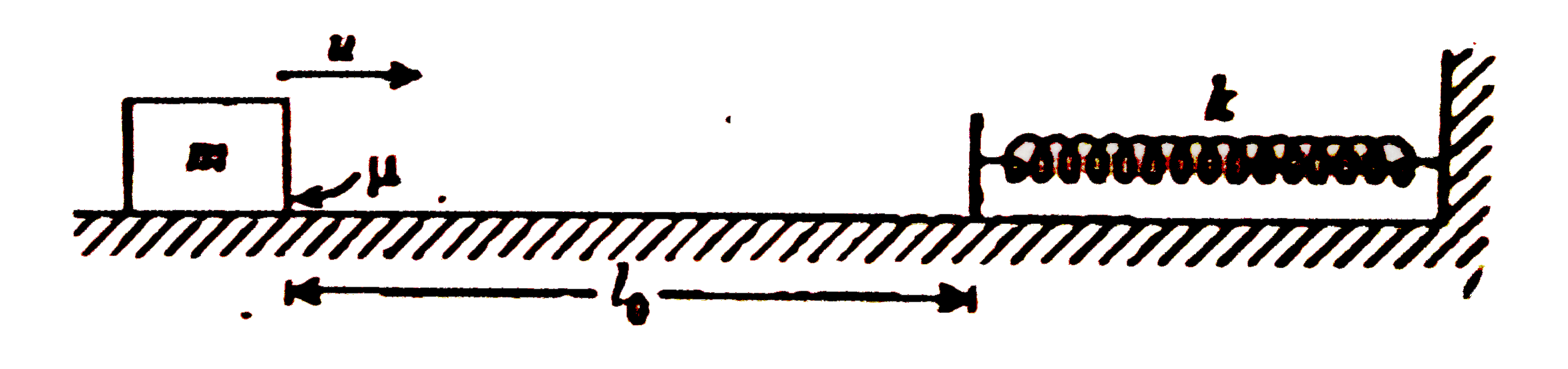 View Solution
View SolutionBlock A of mass m is placed on a plank B. A light support S is fixed on plank B and is attached with the block A with a spring of spring constant K. Consider that initially spring is in its natural length. If the plank B is given an acceleration a, then maximum compression in the spring is xmak. Find the value of x (All the surface are smooth)
 View Solution
View SolutionA block of mass m is attached to the two springs in vertical plane as shown in the figure - 3.95. If initially both the springs are at their natural lengths then velocity of the block is maximum at displacement x given as
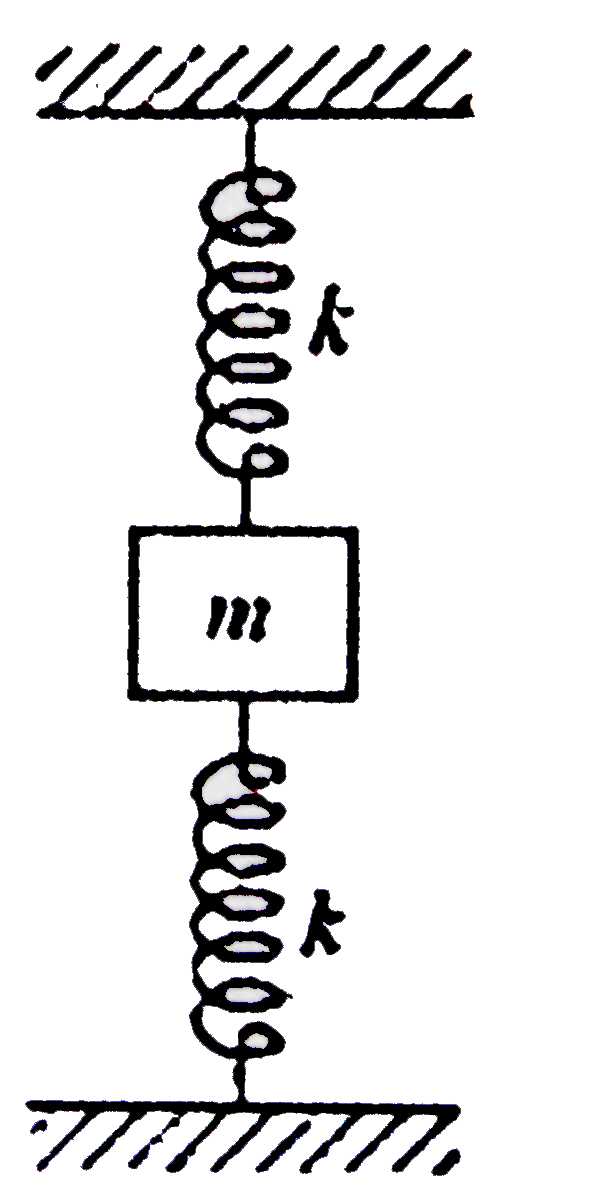 View Solution
View Solution
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x thenView Solution

