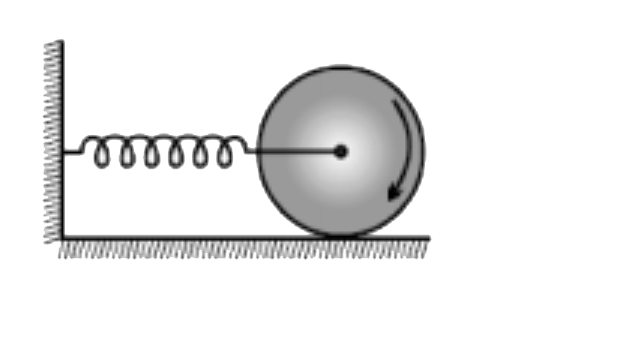
One end of spring of spring constant k is attached to the centre of a disc of mass m and radius R and the other end of the spring connected to a rigid wall. A string is wrapped on the disc and the end A of the string (as shown in the figure) is pulled through a distance a and then released.
The disc is placed on a horizontal rough surface and there is no slipping at any contact point. What is the amplitude of the oscillation of the centre of the disc?

a/2

none of these

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

A string is wrapped on a uniform disc and the other end of the string connected to a wall. The system is placed on a smooth plane, inclined at an angle $θ$ , with the string parallel to the plane, as shown in the figure. The acceleration of the disc is
A $\frac{1}{3} g sin θ$
B $\frac{1}{2} g sin θ$
C $\frac{2}{3} g sin θ$
D $\frac{1}{3} g sin θ$
A disc of mass M and radius R has a spring of constant k attached to its center , the other end of the spring being fixed to a vertical wall. If the disk rolls without slipping on a level floor, how far to the right does the centre of mass move , if Initially the spring was unstretched and the angular speed of the disc was $ω_{0}$

A $R ω \sqrt{(2 M / 3 k)}$
B $R ω \sqrt{(3 M / 2 k)}$
C $R ω \sqrt{(M / k)}$
D $R ω \sqrt{(M / 2 k)}$