Two blocks of masses m and M are connected by means of a metal wire passing over a frictionless fixed pulley. The area of cross-section of the wire is 6.5×10−9m2 and its breaking stress is 2×109Nm−2. If m = 1kg, then calculate the maximum value of M (g=10m/s2)
Mg- T = Ma …(i)
T−mg=ma …(ii)
T=2Mmg(M+m)⇒TA=2MmgA(M+m)=2mgA(1+mM)=2×109
⇒M=1.86kg

Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Matrix Match Type11videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise28videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reason type1videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I20videos
SEMICONDUCTOR AND DEVICE
- BOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS747videos
TEST PAPERS
Similar Questions
Two block of mass m and M are connected means of a metal of a metal wire passing over a frictionless fixed pulley. The area of cross section of the wire is 6.67×10−9m2 and its breaking stress is 2×109Nm−2. If m = 1kg. Find the maximum value of M in kg for which the wire will not break. (g=10m/s2).
View SolutionTwo block of mass m and M are connected means of a metal of a metal wire passing over a frictionless fixed pulley. The area of cross section of the wire is 6.67×10−9m2 and its breaking stress is 2×109Nm−2. If m = 1kg. Find the maximum value of M in kg for which the wire will not break. (g=10m/s2).
View Solution
Knowledge Check
- Question 1 - Select One
Two blocks of masses m and 2m are connected through a wire fo breakig stress S passing over a frictionless pulley. The maximum radius of the wire to be used so that the wire may not break is
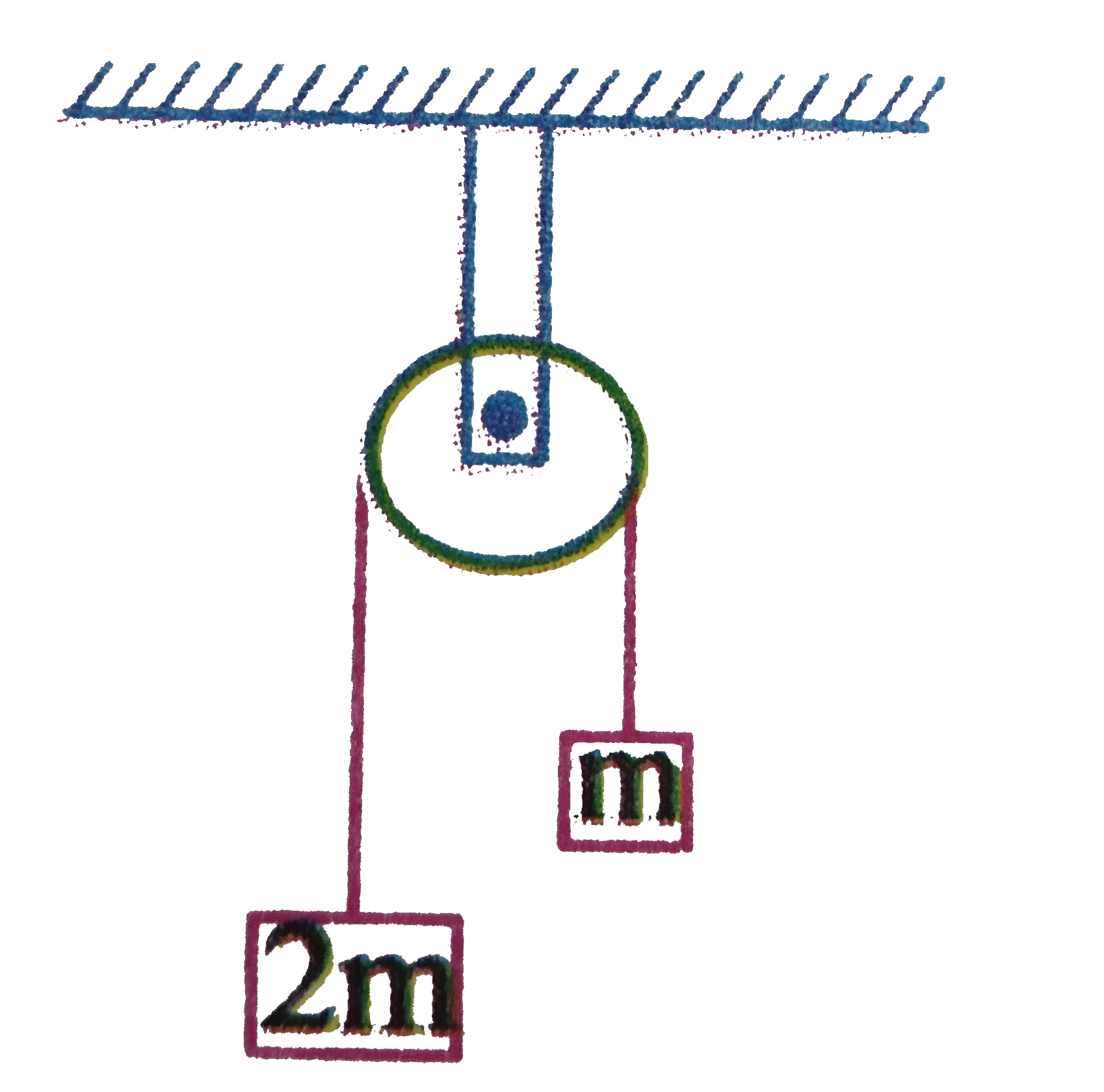 A√34mgπSB√43mgSC√433gπSD√12mgπS
A√34mgπSB√43mgSC√433gπSD√12mgπS - Question 2 - Select One
Two blocks of masses 5 kg and 10 kg are connected by a metal wire going over a smooth pulley as shown in the figure. The breaking stress of the metal wire is 2×109N m−2. If g=10ms−2, then what is the minimum radius of the wire which will not break
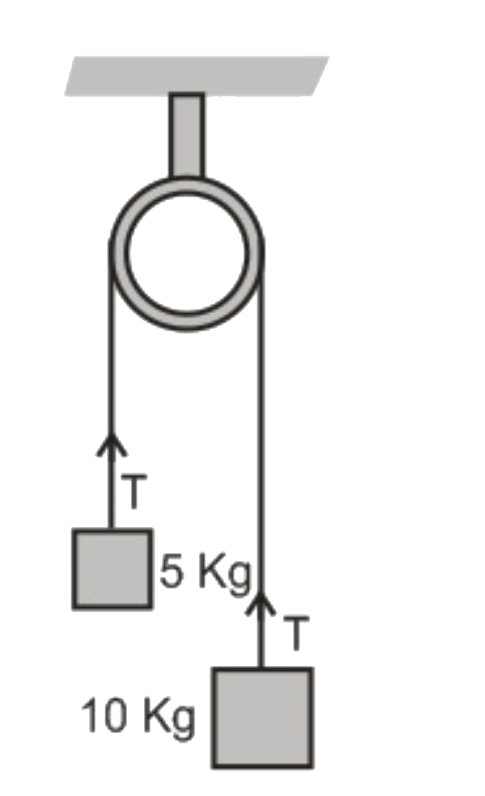 A0.1 mmB0.2 mmC0.05 mmD0.25 mm
A0.1 mmB0.2 mmC0.05 mmD0.25 mm - Question 3 - Select One
Two blocks of masses 1kg and 2kg are connected by a metal wire going over a smooth pulley as shown in figure.
The breaking stress of the metal is (40/3π)×106N/m2. If g=10ms−2, then what should be the minimum radius of the wire used if it is not to break?
 A0.5 mmB1 mmC1.5 mmD2 mm
A0.5 mmB1 mmC1.5 mmD2 mm
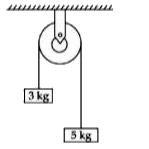
Two blocks of masses 3 kg and 5 kg are connected by a metal wire going over a smooth pulley. The breaking stress of the metal is 24π×102Nm−2 . What is the minimum radius of the wire ?
(take g=10ms−2)
 View Solution
View SolutionA wire of length 1m is stretched by a force of 10N. The area of cross-section of the wire is 2×10–6m2 and Y is 2×1011N/m2 . Increase in length of the wire will be -
View SolutionTwo blocks of masses 5 kg and 10 kg are connected by a metal wire going over a smooth pulley as shown in the figure. The breaking stress of the metal wire is 2×109N m−2. If g=10ms−2, then what is the minimum radius of the wire which will not break
 View Solution
View SolutionTwo blocks of masses 1kg and 2kg are connected by a metal wire going over a smooth pulley as shown in figure.
The breaking stress of the metal is (40/3π)×106N/m2. If g=10ms−2, then what should be the minimum radius of the wire used if it is not to break?
 View Solution
View SolutionTwo blocks of masses 1kg and 2kg are connected by a metal wire goijng over a smooth pulley as shown in figure.
The breaking stress of the metal is (40/3π)×106N/m2. If g=10ms−12, then what should be the minimum radlus of the wire used if it is not to break?
 View Solution
View Solution

