Two block of mass m and M are connected means of a metal of a metal wire passing over a frictionless fixed pulley. The area of cross section of the wire is 6.67×10−9m2 and its breaking stress is 2×109Nm−2. If m = 1kg. Find the maximum value of M in kg for which the wire will not break. (g=10m/s2).
The correct Answer is:2
To solve the problem, we need to find the maximum value of mass M such that the wire does not break when two blocks of mass m and M are connected by the wire over a frictionless pulley.
1. Identify the Given Values:
- Mass of block m=1kg
- Area of cross-section of the wire A=6.67×10−9m2
- Breaking stress of the wire σ=2×109N/m2
- Acceleration due to gravity g=10m/s2
2. Calculate the Maximum Tension in the Wire:
The breaking stress is defined as the maximum tension per unit area that the wire can withstand:
Tmax=σ×A
Substituting the given values:
Tmax=(2×109N/m2)×(6.67×10−9m2)=13.34N
3. Set Up the Equations of Motion:
For the system of two blocks, the forces acting on them can be described as follows:
- For mass M (downward motion):
Mg−T=Ma(1)
- For mass m (upward motion):
T−mg=ma(2)
4. Add the Two Equations:
Adding equations (1) and (2):
(Mg−T)+(T−mg)=Ma+ma
This simplifies to:
(M−m)g=(M+m)a
Rearranging gives:
a=(M−m)gM+m(3)
5. Substitute for Tension T:
From equation (2), we can express T in terms of a:
T=mg+ma
Substituting equation (3) into this:
T=mg+m((M−m)gM+m)
Simplifying this:
T=mg(1+(M−m)M+m)=mg(M+m+M−mM+m)=mg(2MM+m)
6. Set T Equal to Tmax:
To find the maximum value of M before the wire breaks, set T=Tmax:
mg(2MM+m)=Tmax
Substituting the known values:
1⋅10(2MM+1)=13.34
Simplifying:
20MM+1=13.34
7. Cross-Multiply and Solve for M:
20M=13.34(M+1)
Expanding:
20M=13.34M+13.34
Rearranging gives:
20M−13.34M=13.34
6.66M=13.34
M=13.346.66≈2kg
Conclusion:
The maximum value of M for which the wire will not break is approximately 2kg.
- Mass of block m=1kg
- Area of cross-section of the wire A=6.67×10−9m2
- Breaking stress of the wire σ=2×109N/m2
- Acceleration due to gravity g=10m/s2
The breaking stress is defined as the maximum tension per unit area that the wire can withstand:
Tmax=σ×A
Substituting the given values:
Tmax=(2×109N/m2)×(6.67×10−9m2)=13.34N
For the system of two blocks, the forces acting on them can be described as follows:
- For mass M (downward motion):
Mg−T=Ma(1)
- For mass m (upward motion):
T−mg=ma(2)
Adding equations (1) and (2):
(Mg−T)+(T−mg)=Ma+ma
This simplifies to:
(M−m)g=(M+m)a
Rearranging gives:
a=(M−m)gM+m(3)
From equation (2), we can express T in terms of a:
T=mg+ma
Substituting equation (3) into this:
T=mg+m((M−m)gM+m)
Simplifying this:
T=mg(1+(M−m)M+m)=mg(M+m+M−mM+m)=mg(2MM+m)
To find the maximum value of M before the wire breaks, set T=Tmax:
mg(2MM+m)=Tmax
Substituting the known values:
1⋅10(2MM+1)=13.34
Simplifying:
20MM+1=13.34
20M=13.34(M+1)
Expanding:
20M=13.34M+13.34
Rearranging gives:
20M−13.34M=13.34
6.66M=13.34
M=13.346.66≈2kg
The maximum value of M for which the wire will not break is approximately 2kg.
Similar Questions
A mass of 20kg is attached to one end of a steel wire 50cm long and is rotated in a horizontal circle. The area of cross-section of the wrie is 10−6m2 and the breaking stress for it is 4.8×107Pa. Calculate the maximum velocity with which the mass can be rotated.
View SolutionTwo blocks of masses m1=4kg and m2=2kg are connected to the ends of a string which passes over a massless, frictionless pulley. The total downwards thrust on the pulley is nearly

View Solution
Knowledge Check
Two blocks of masses 1kg and 2kg are connected by a metal wire going over a smooth pulley as shown in figure.
The breaking stress of the metal is (40/3π)×106N/m2. If g=10ms−2, then what should be the minimum radius of the wire used if it is not to break?
 A0.5 mmB1 mmC1.5 mmD2 mm
A0.5 mmB1 mmC1.5 mmD2 mm
Two blocks of masses 5 kg and 10 kg are connected by a metal wire going over a smooth pulley as shown in the figure. The breaking stress of the metal wire is 2×109N m−2. If g=10ms−2, then what is the minimum radius of the wire which will not break
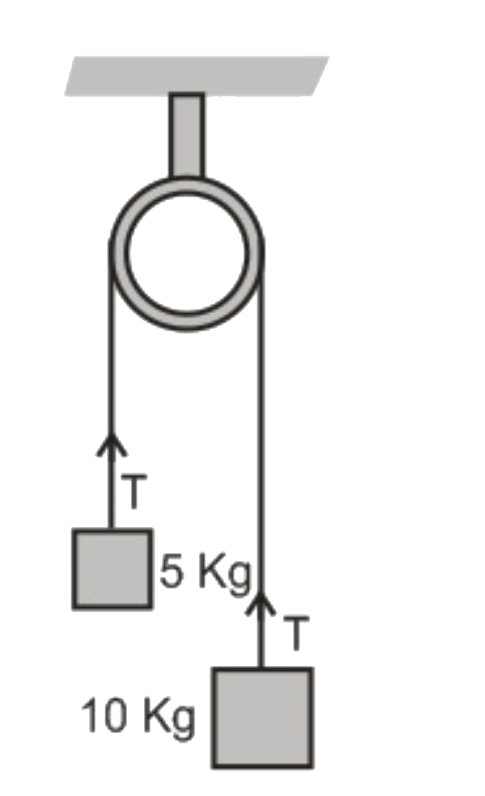
View SolutionTwo masses 7 kg and 12 kg are connected at the two ends of a metal wire that goes ove a frictionless puulley. What should be in the minimum radius of the wire in order that the wire does not break,if the breaking stess of the metal is 1.3×108N/m2 ?
View SolutionThe resistivity of a potentiometer wire is 40×10−8Ω−m and its area of cross section is 8×10−6m2. If 0.2 A current is flowing through the wire the potential gradient will be
View SolutionTwo blocks of masses 1kg and 2kg are connected by a metal wire going over a smooth pulley as shown in figure.
The breaking stress of the metal is (40/3π)×106N/m2. If g=10ms−2, then what should be the minimum radius of the wire used if it is not to break?

View SolutionTwo blocks of masses 2 kg and 3kg are connected by a metal wire going over a smoother pulley as shown in figure. The breaking stress of the steel is 2×109Nm−2. What would be the minimum radius of the wire used if it not to break ? Take ,g=10ms−2
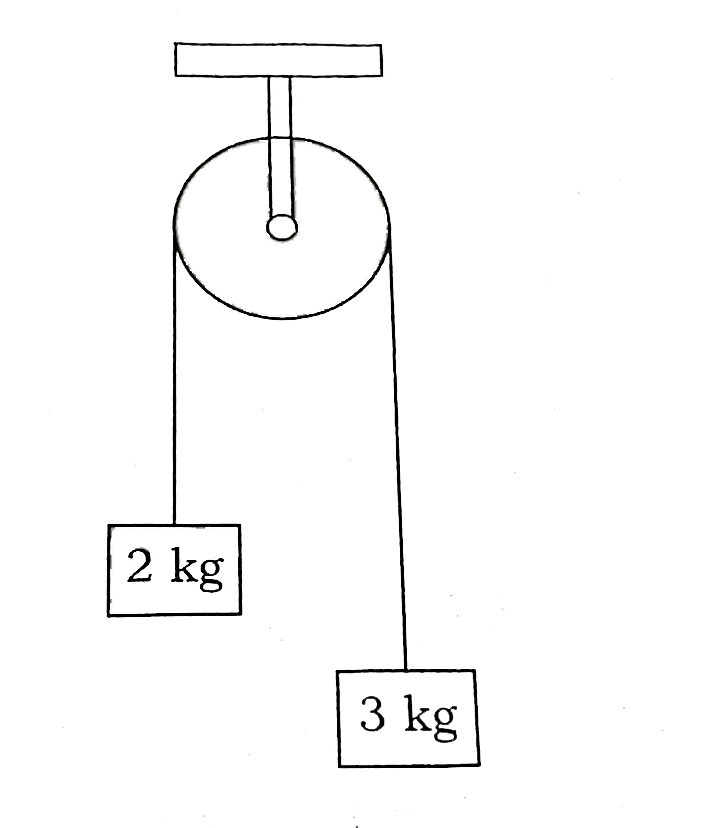
View SolutionA wire of length l = 3m and area of cross section 10−2cm2 and breaking stress 4.8×10−7Nm2 is attached with block of mass 10kg. Find the maximum possible value of angular velocity with which block can be moved in circle with string fixed at one end.
View SolutionA steal wire of cross-section area 3×10−6m2 can withstand a maximum strain of 10−3 .Young's modulus of steel is 2×1011Nm−2 .The maximum mass this wire can hold is
View Solution
