One mole of a moatomic idal gas is taken through the cycle shown in figure.

A→B Adiabatic expansion
B→C Cooling at constant volume
C→D Adiabatic compression
D→A Heating at constant volume
The pressure and temperature at A,B etc, are denoed by PA,TA,PB,TB respectively Given TA=1000K,PB=(2/3)PA and PC=(1/3)PA. Calculate
a. The work done by the gas in the process A→B
b. The heat lost by the gas inthe process B→C and
c. temperature TD given (2/3)2/4=0.85 and R−8.31 J/mol K.
a. As for adiabatic change PVγ= constant
i.e.P(μRTP)γ= constant [as PV=μRT]
i.e. TγPγ−1= constant so (TBTA)γ=(PBPA)γ−1 with γ=53
i.e. TB=TA(23)1−1T=1000(23)2/5=850K
So WAB=μR[TB−TA][1−γ]=1×8.31[1000−850][(5/3)−1]
i.e. WAB=(3/2)×8.31×150=1869.75J
b. for B→C V= constant so ΔW=0
So from first law of thermodynamics
ΔQ=ΔU+De<AW=μCvΔT+0
or ΔQ=1×(32R)(Tc−850) as Cv=32R
Now along path BC, V= constant P∝T
i.e. PCPB=TCTB,TC=(1/3)PA(2/3)PA×TB=(TB)?2=8502=425K
So ΔQ=1×32×8.31(425−850)=−5297.625J
[Negative heat means, heat is lost by the system]
c. As A and D are on the same isochoric
PDPA=TDTai.e.PD=PATDTA
or (TD)1/2=TC[PAPCTA]1−1γ i.e. T35D=(TB2)[PA(1/3)PA1000]25
i.e. T35D=⎡⎣12(23)25×1000⎤⎦[31000]25 i.e. TD=500K
Topper's Solved these Questions
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - SOLVED PROBLEMS OBJECTIVE
15 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - COMPREHENSION TYPE
5 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question
2 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - NUMERICAL BASED QUESTIONS DECIMAL TYPE
5 Videos
Similar Questions
One mole of a monoatomic ideal gas is taken through the cycle shown in Fig:
A→B: adiabatic expansion
B→C: cooling at constant volume
C→D: adiabatic compression
D→A: heating at constant volume
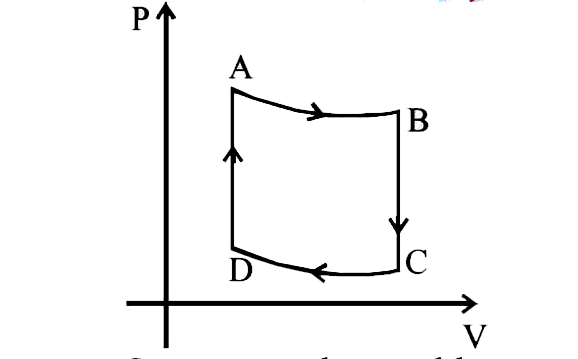
The pressure and temperature at A,B,etc. are denoted by PA,TA,PB,TBetc. respectively. Given that TA=1000K, PB=(2/3)PAandPC=(1/3)PA, calculate the following quantities:
(i) The work done by the gas in the process A→B
(ii) The heat lost by the gas in the process B→C.
(iii) The temperature TD. [Given :(2/3)2/5=0.85]
View SolutionOne mole of a monoatomic ideal gas is taken through the cycle shown in Fig:
A→B: adiabatic expansion
B→C: cooling at constant volume
C→D: adiabatic compression
D→A: heating at constant volume

The pressure and temperature at A,B,etc. are denoted by PA,TA,PB,TBetc. respectively. Given that TA=1000K, PB=(2/3)PAandPC=(1/3)PA, calculate the following quantities:
(i) The work done by the gas in the process A→B
(ii) The heat lost by the gas in the process B→C.
(iii) The temperature TD. [Given :(2/3)2/5=0.85]
View SolutionOne mole of a monoatomic ideal gas is taken through the cycle shown in figure.
A→B Adiabatic expansion
B→C Cooling at constant volume
C→D Adiabatic compression.
D→A Heating at constant volume
The pressure and temperature at A,B etc., are denoted by pA,TA,pB,TB etc. respectively.
Given, TA=1000K, pB=(23)pA and pC=(13)pA. Calculate
(a) the work done by the gas in the process A→B
(b) the heat lost by the gas in the process B→C
Given, (23)0.4=0.85 and R=8.31J/mol−K
View SolutionOne mole of a monoatomic ideal gas is taken through the cycle shown in figure.
A→B Adiabatic expansion
B→C Cooling at constant volume
C→D Adiabatic compression.
D→A Heating at constant volume
The pressure and temperature at A,B etc., are denoted by pA,TA,pB,TB etc. respectively.
Given, TA=1000K, pB=(23)pA and pC=(13)pA. Calculate
(a) the work done by the gas in the process A→B
(b) the heat lost by the gas in the process B→C
Given, (23)0.4=0.85 and R=8.31J/mol−K
View SolutionOn mole of a monoatomic ideal gas is taken through the cycle shown in figure .
A→B : Adiabatic expansion B→C : Cooling at constant volume
C→D: Adiabatic compression D→A : Heating at constant volume
The pressure and temperature at A,B, etc, are denoted by PA,TA,PB,TB etc., respectively . Given that TA=1000K,PB=(23)PAandPC=(13)PA. Calculate the following quantities: (i) The work done by the gas in the processs A→B (ii) The heat lost by the gas in the process B→C (iii) The temperature TD.(Given:(23)2/5=0.85)
<
View SolutionOn mole of a monoatomic ideal gas is taken through the cycle shown in figure .
A→B : Adiabatic expansion B→C : Cooling at constant volume
C→D: Adiabatic compression D→A : Heating at constant volume
The pressure and temperature at A,B, etc, are denoted by PA,TA,PB,TB etc., respectively . Given that TA=1000K,PB=(23)PAandPC=(13)PA. Calculate the following quantities: (i) The work done by the gas in the processs A→B (ii) The heat lost by the gas in the process B→C (iii) The temperature TD.(Given:(23)2/5=0.85)
_E01_271_Q01.png)
View SolutionOne mole of a monatomic ideal gas is taken through the cycle shown in the figure: A→B adiabatic expansion

B→C: cooling at constant volume
C→D adiabatic compression D→C: heating at constant volume.
The pressure and temperature at PA,PB etc. TA,TB etc. are denoted etc. respectively. Given that
TA=1000K,PB=(2/3)PA and PC=(1/3)PA
Calculate the following quantities.
The work done by the gas in process A→B (in J)
View Solution
The pressure at C is
View SolutionOne mole of a monatomic ideal gas is taken through the cycle shown in the figure: A→B adiabatic expansion
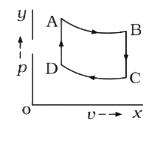
B→C: cooling at constant volume
C→D adiabatic compression D→C: heating at constant volume.
The pressure and temperature at PA,PB etc. TA,TB etc. are denoted etc. respectively. Given that
TA=1000K,PB=(2/3)PA and PC=(t/3)PA
Calculate the following quantities.
The heat lost by the gas in process B→C (in J)
View SolutionOne mole of a monatomic ideal gas is taken through the cycle shown in the figure: A→B adiabatic expansion

B→C: cooling at constant volume
C→D adiabatic compression D→C: heating at constant volume.
The pressure and temperature at PA,PB etc. TA,TB etc. are denoted etc. respectively. Given that
TA=1000K,PB=(2/3)PA and PC=(t/3)PA
Calculate the following quantities.
The heat lost by the gas in process B→C (in J)
View Solution
