A body with an initial temperature θ1 is allowed to cool in a surrounding which is at a constant temperature of θ0(θ<θ1) Assume that Newton's law of cooling is obeyed Let k= constant The temperature of the body after time t is best experssed by .
(θ1−θ0)e−kt
(θ1−θ0)In(kt)
θ0+(θ1−θ0)e−kt
θ1e−kt=θ0
dθdt=−k(θ−θ0)
∫θθ1dθθ−θ0=−k∫10dt=θ=θ0+(θ1−θ0)e−kt
Hence c is correct.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - COMPREHENSION TYPE5videos
HEAT AND TEMPERATURE
- BOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - ASSERTION REASON TYPE1videos
HEAT AND TEMPERATURE
- BOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - SOLVED PROBLEMS SUBJECTIVE18videos
HEAT AND TEMPERATURE
- BOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question2videos
GRAVITATION
- BOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - NUMERICAL BASED QUESTIONS DECIMAL TYPE5videos
KINEMATICS
Similar Questions
Knowledge Check
- Question 1 - Select One
Newton's law of cooling holds good provided the temperature difference between the body and the surroundings is .
AlargeBsmallCvery largeDany value - Question 2 - Select One
If a piece of metal is heated to temperature θ and the allowed to cool in a room which is at temperature θ0, the graph between the temperature T of the metal and time t will be closet to
A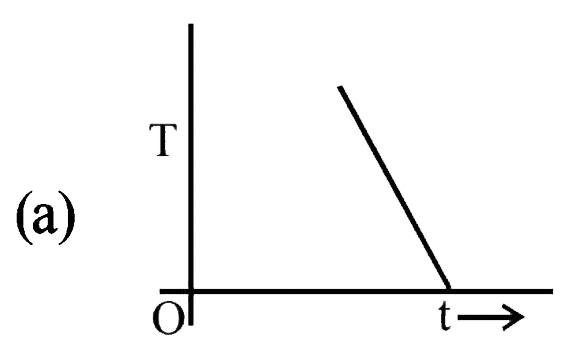 B
B C
C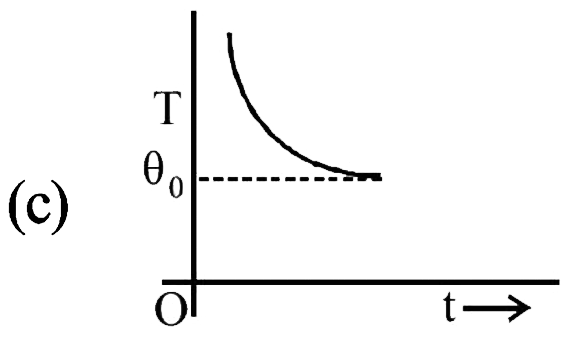 D
D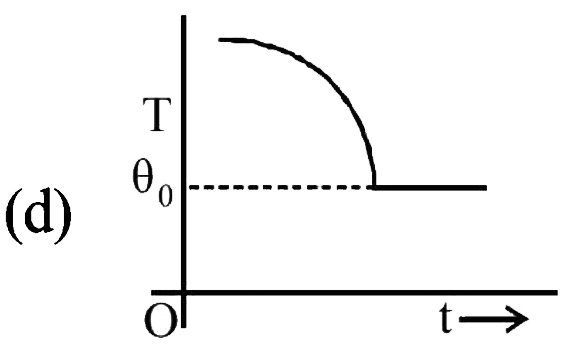
- Question 3 - Select One
A body cools from a temperature 3T to 2T in 10 minutes. The room temperature is T. Assume that Newton's law of cooling is applicable. The temperature of the body at the end of next 10 minutes will be
A43TBTC74TD32T
A body cools in a surrounding which is at a constant temperature of θ0 Assume that it obeys Newton's law of cooling Its temperature θ is plotted against time t Tangents are drawn to the curve at the points P(θ=θ1) and Q(θ=θ2) These tangents meet the time axis at angle of ϕ2 andϕ1 as shown
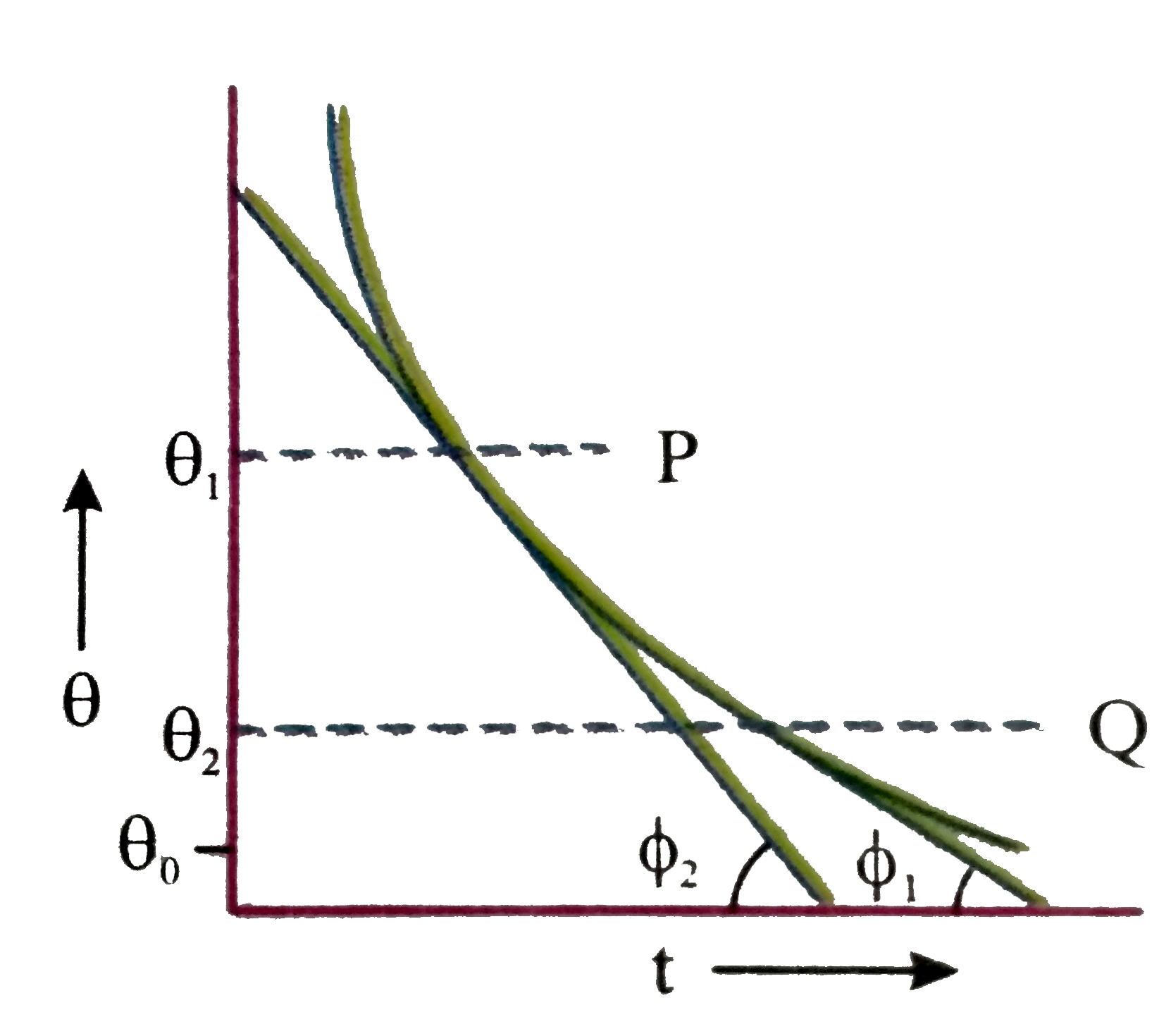 .View Solution
.View SolutionA body cools in a surrounding which is at constant temperature of θ0. Assume that it obeys Newyon's law of colling. Its temperature θ is plotted against time t. Tangents are drawn to the curve at the points P(θ=θt) and Q(θ=θ2). These tangents meet the time axis at angles of ϕ2 and ϕ1, as shown
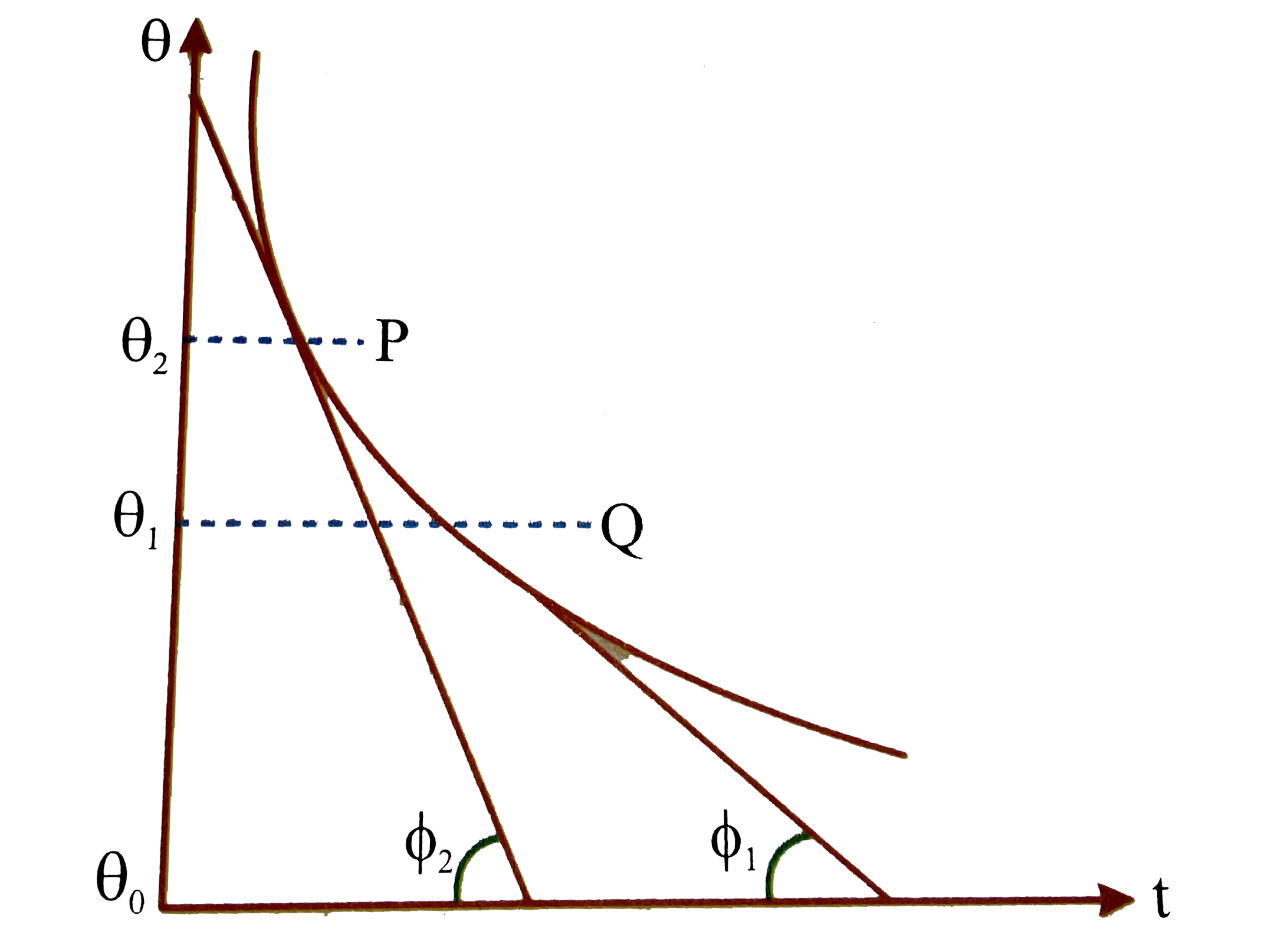 View Solution
View SolutionA body is heated to a temperature of 75∘C and is allowed to cool. If the temperature of the surrounding is 35∘C, then the temperature at which the rate of cooling will be exactly half of that initially will be
View SolutionA liquid takes 10 minutes to cool from 80∘C to 50∘C. The temperature of the surroudings is 20∘C. Assuming that the Newton's law of cooling is obeyed, the cooling constant will be -
View SolutionA body cools from 60∘C to 50∘C in 10 minutes . If the room temperature is 25∘C and assuming Newton's law of cooling to hold good, the temperature of the body at the end of the next 10 minutes will be
View Solution

