A fixed mass of a gas is taken through a process A→B→C→A . Here A→B isisobaric. B→C is aiabatic and C→A is isothermal. Find eficiency of the process (take γ=1.5)
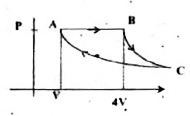
The correct Answer is:3−2In23
Topper's Solved these Questions
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) (LEVEL-I)
50 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) (LEVEL-I) (ASSERTION AND REASON)
2 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) (level-1) (TRUE OR FALSE QUESTIONS)
6 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question
2 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - NUMERICAL BASED QUESTIONS DECIMAL TYPE
5 Videos
Similar Questions
A fixed mass of gas is taken through a process A→B→C→A. Here A→B is isobaric, B→C is adiabatic and C→Ais isothermal. Find work done is the process ( take γ=1.5).
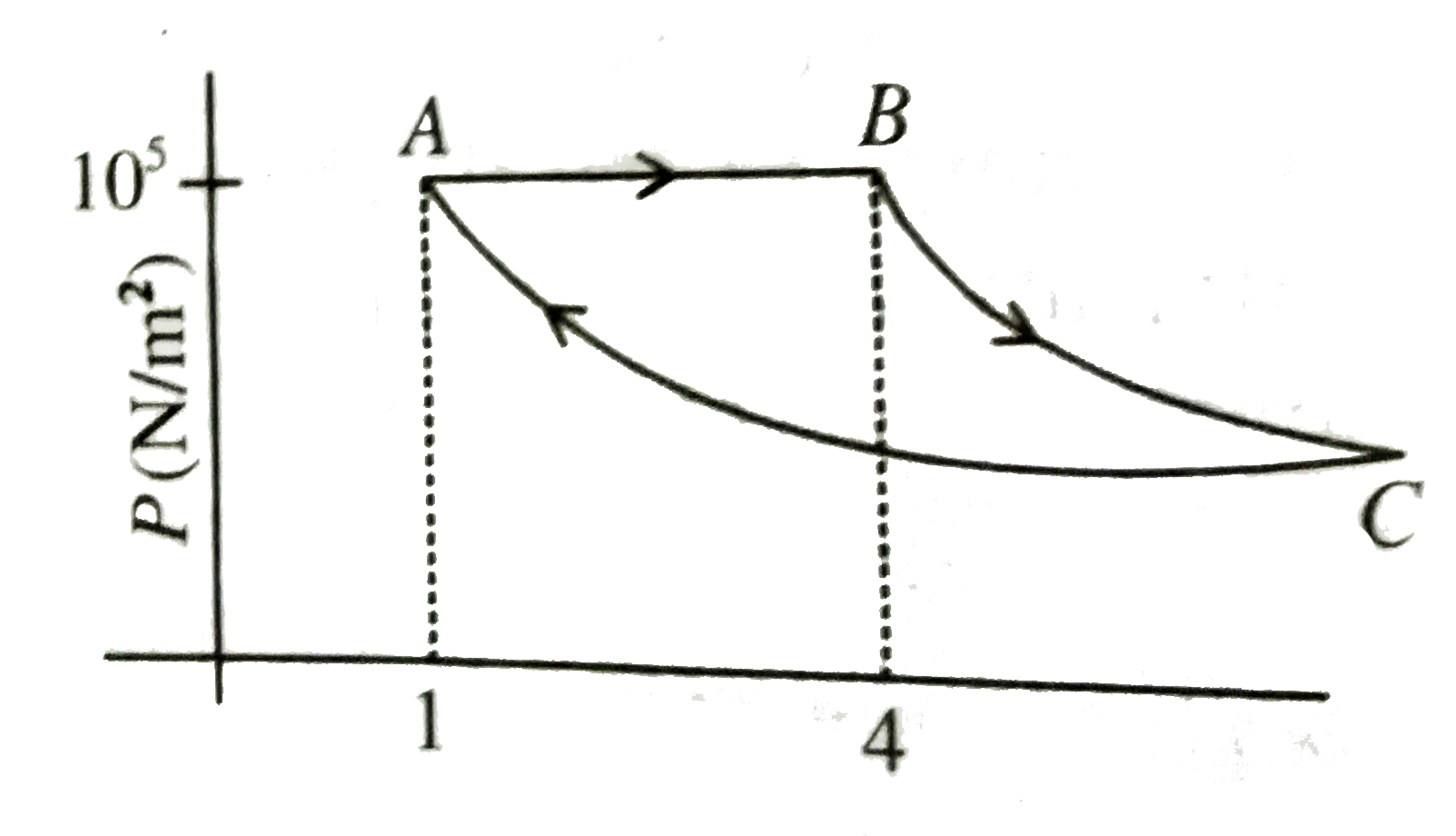
View SolutionA fixed mass of gas is taken through a process A→B→C→A. Here A→B is isobaric, B→C is adiabatic and C→Ais isothermal. Find volume at C.
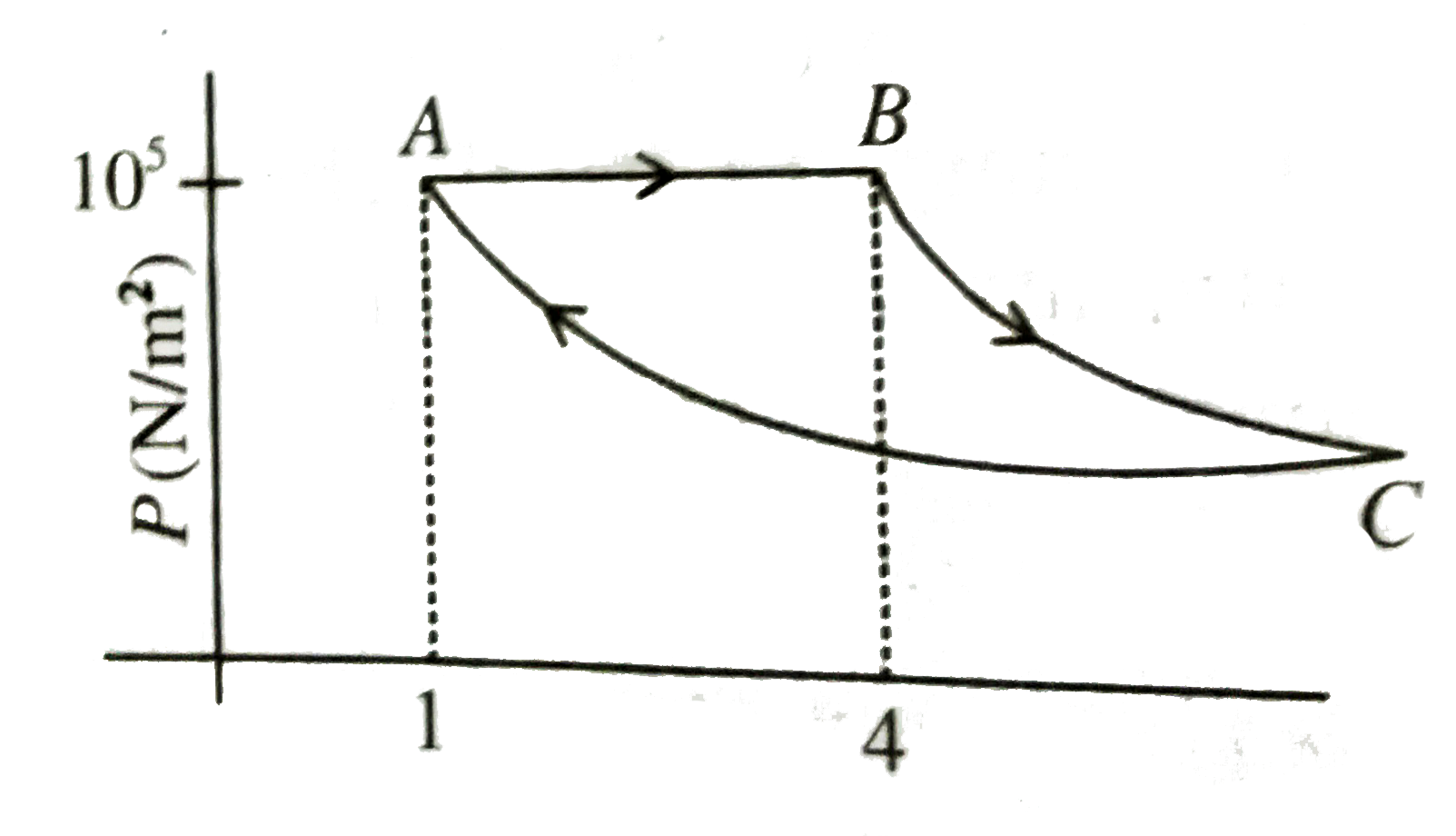
View Solution
Knowledge Check
A fixed mass of gas is taken through a process A→B→C→A. Here A→B is isobaric, B→C is adiabatic and C→Ais isothermal.

Find work done is the process ( take γ=1.5).A4.9×105JB3.2×105JC1.2×105JD7.2×105JA fixed mass of gas is taken through a process A→B→C→A. Here A→B is isobaric, B→C is adiabatic and C→Ais isothermal.
 Find volume at C. A32m3B100m3C64m3D25m3
Find volume at C. A32m3B100m3C64m3D25m3A fixed mass of gas is taken through a process A→B→C→A. Here A→B is isobaric, B→C is adiabatic and C→Ais isothermal.
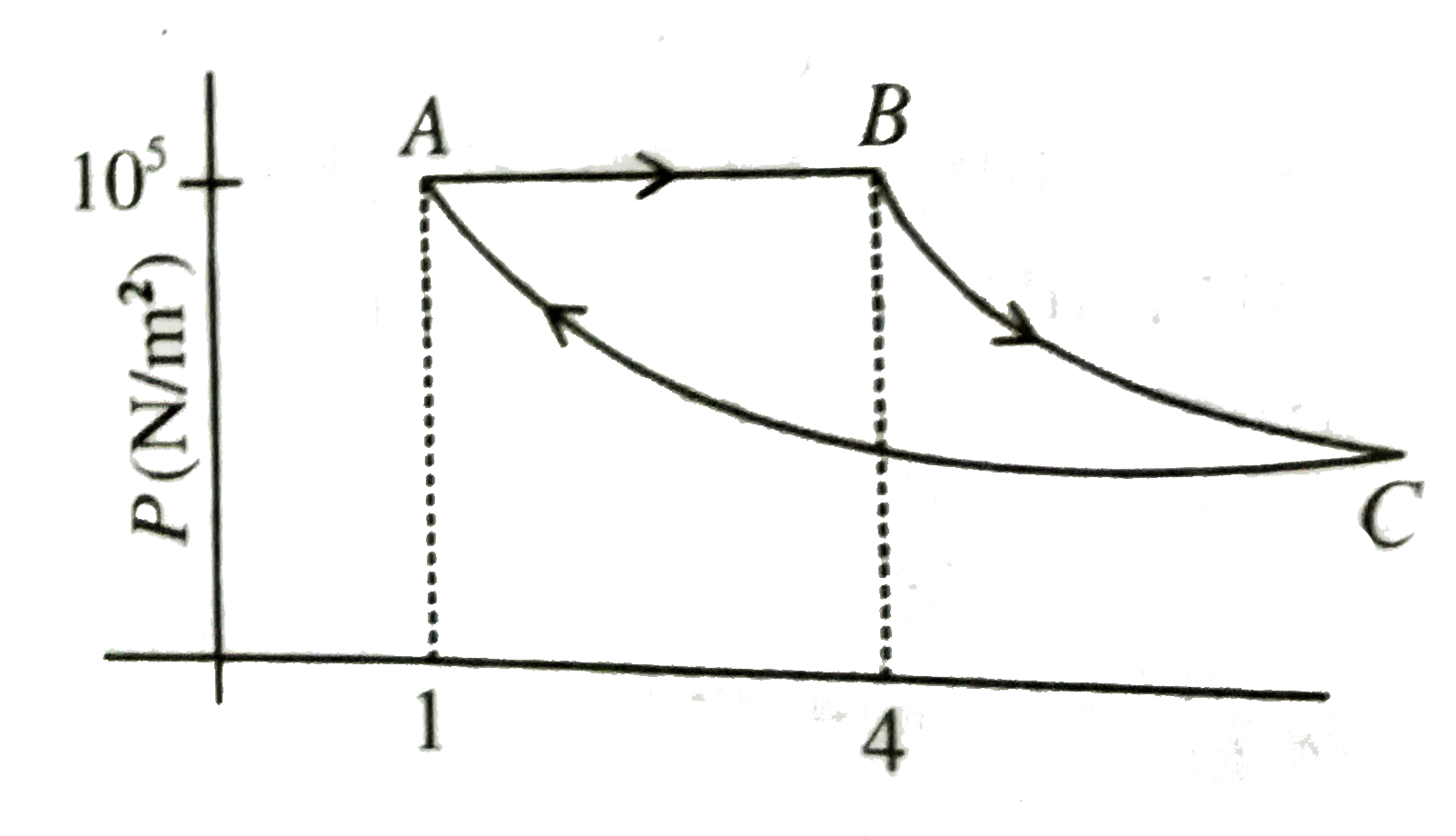
Find pressure at C.A10564N/m2B10532N/m2C10512N/m2D1056N/m2
A fixed mass of gas is taken through a process A→B→C→A. Here A→B is isobaric, B→C is adiabatic and C→Ais isothermal. Find pressure at C

.
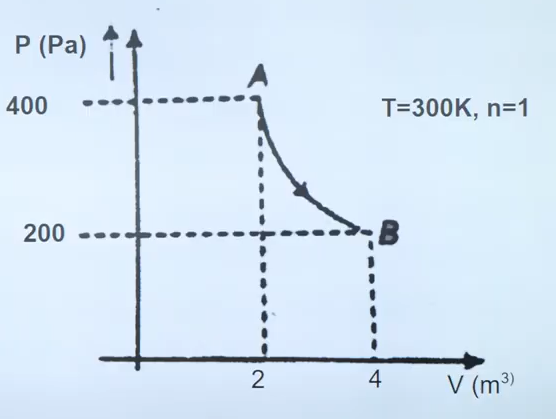
View SolutionA gas is taken through an isothermal process as shown.Find the work done by the gas
View SolutionOne mole of a diatomic ideal gas (γ=1.4) is taken through a cyclic process starting from point A. The process A→B is an adiabatic compression, B→C is isobaric expansion, C→D is an adiabatic expansion, and D→A is isochoric. The volume ratios are VA/VB=16andVC/VB=2 and the temperature at A is TA=300K. Calculate the temperature of the gas at the points B and D and find the efficiency of the cycle.
View SolutionOne mole of a diatomic ideal gas (γ=1.4) is taken through a cyclic process starting from point A. The process A→B is an adiabatic compression, B→C is isobaric expansion, C→D is an adiabatic expansion, and D→A is isochoric. The volume ratios are VA/VB=16andVC/VB=2 and the temperature at A is TA=300K. Calculate the temperature of the gas at the points B and D and find the efficiency of the cycle.
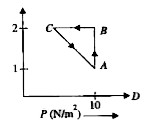
View SolutionAn ideal gas is taken through cycle A→B→C−A, as shown in Fig. IF the net heat supplied to the gas in the cycle is 5 J, the work done by the gas in the process C→A is
View Solution
