A fixed mass of gas is taken through a process A→B→C→A. Here A→B is isobaric, B→C is adiabatic and C→Ais isothermal. Find pressure at C
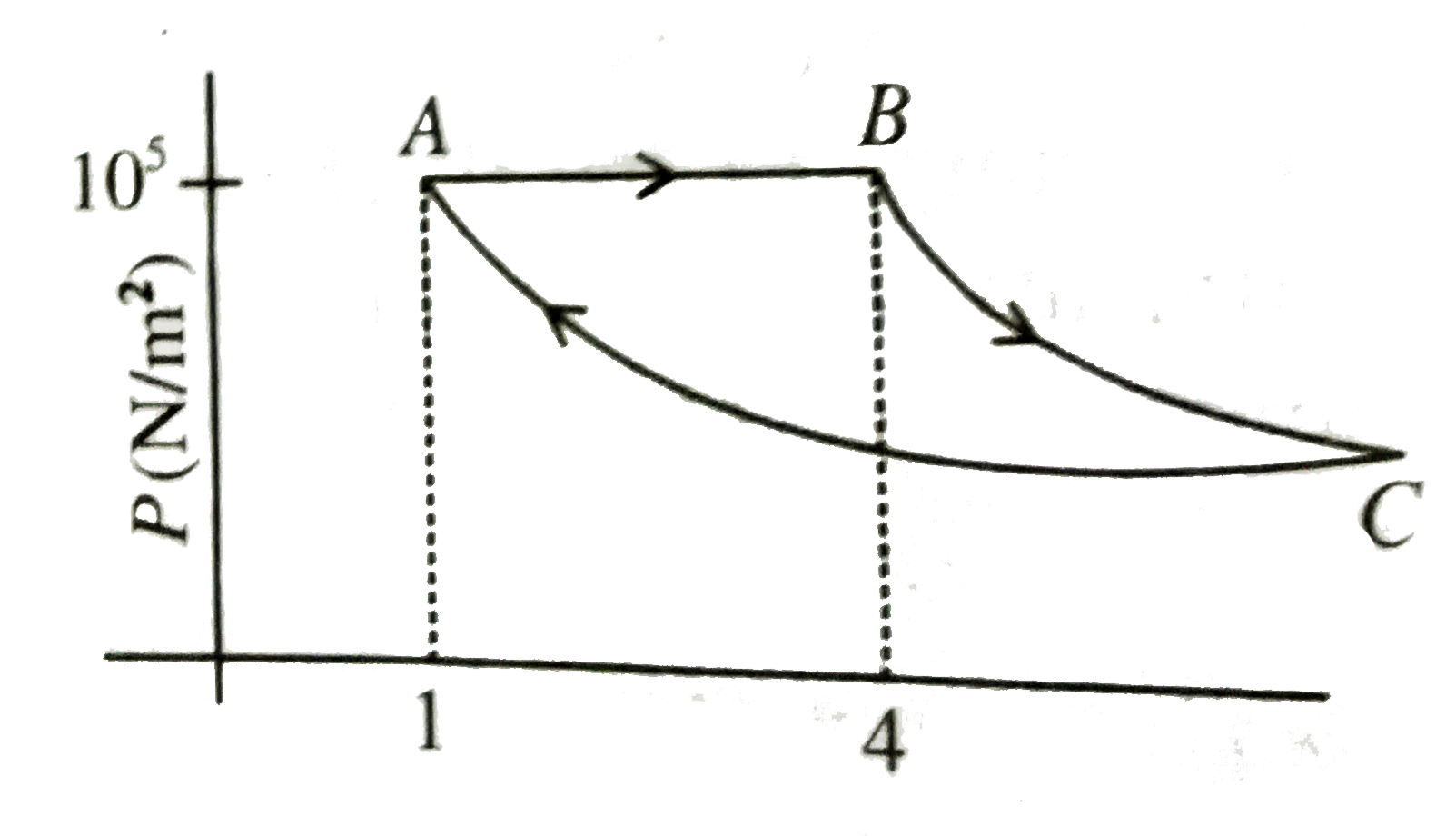
.
10564N/m2
10532N/m2
10512N/m2
1056N/m2
The correct Answer is:A
a For adiabatic process BC,
PB=PC ...(i)
For isothermal process CA
PAVA=PCVC ...(ii)
From Eqs. (i) and (ii)
VC=[VγBVA]1γ−1=64m3
PC=PAVAVC=10564N/m2
b Work done, W=WAB+WBC+WCA
=P(VB−VA)+1γ−1[PVB−PCVC+PVA1n(VA/VC)]
Putting the values,
W=4.9×105J
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Assertion-Reasoning6videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type14videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
Similar Questions
A fixed mass of gas is taken through a process A→B→C→A. Here A→B is isobaric, B→C is adiabatic and C→Ais isothermal. Find volume at C.
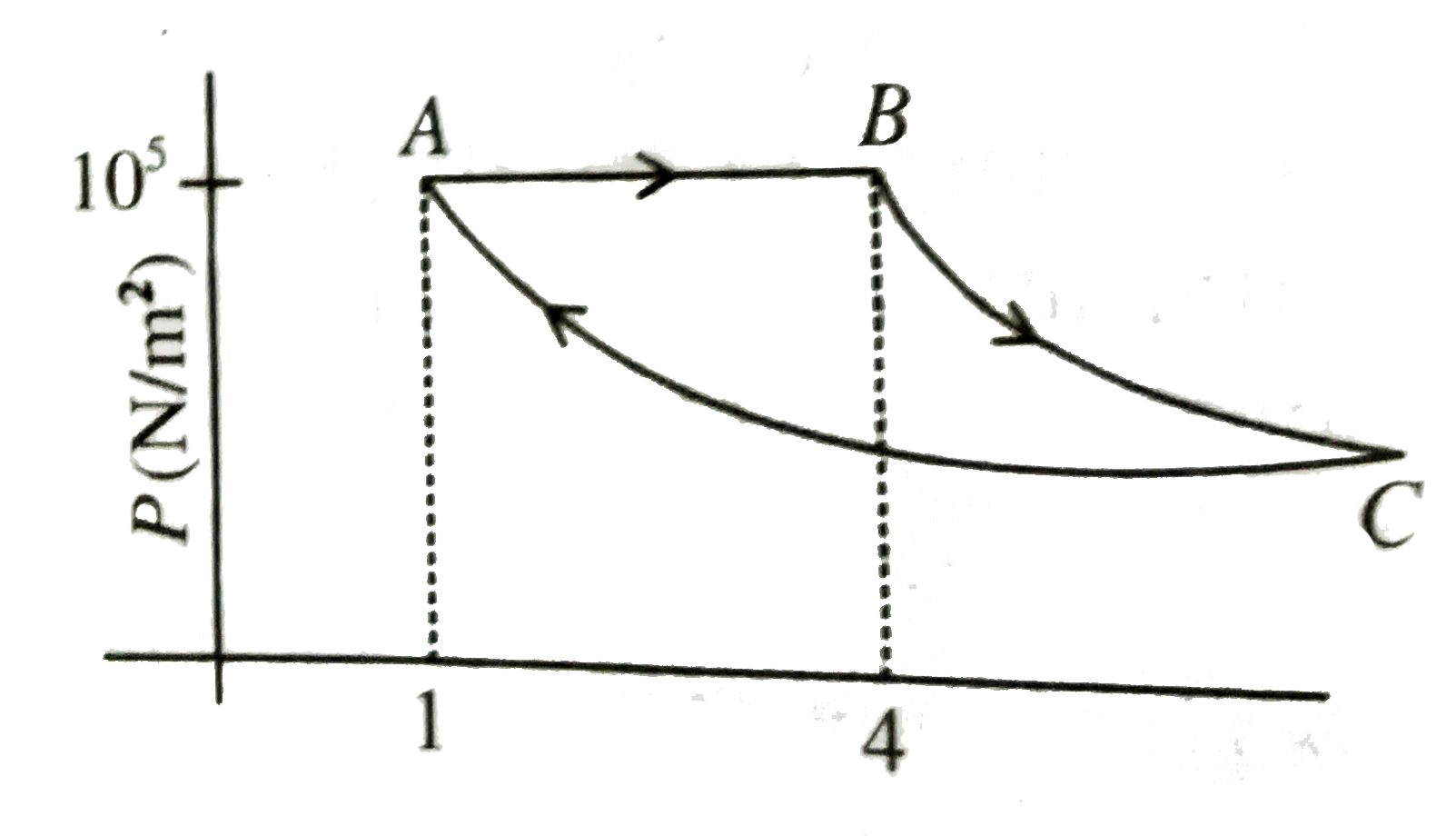 View Solution
View SolutionA fixed mass of gas is taken through a process A→B→C→A. Here A→B is isobaric, B→C is adiabatic and C→Ais isothermal. Find work done is the process ( take γ=1.5).
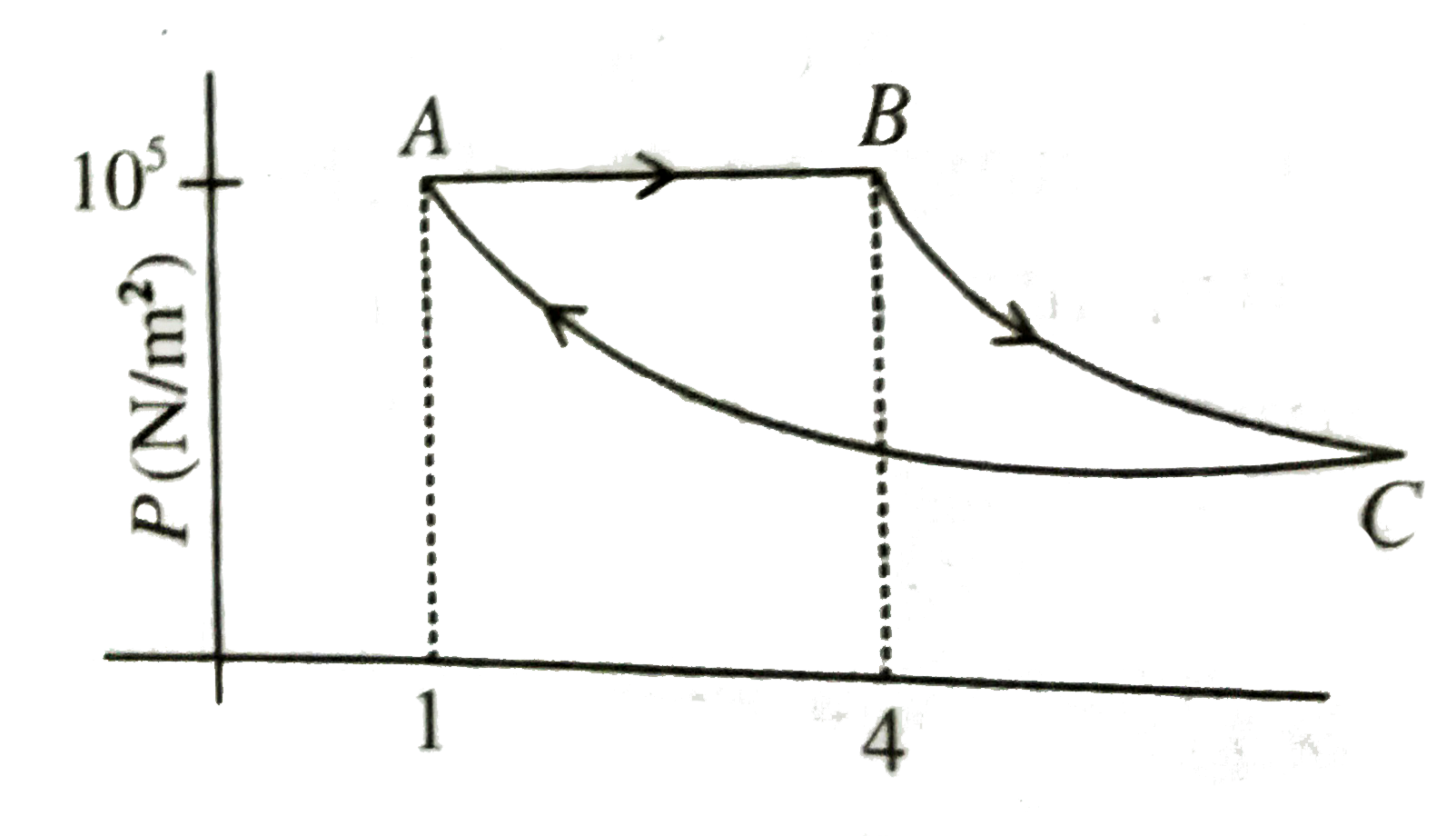
View Solution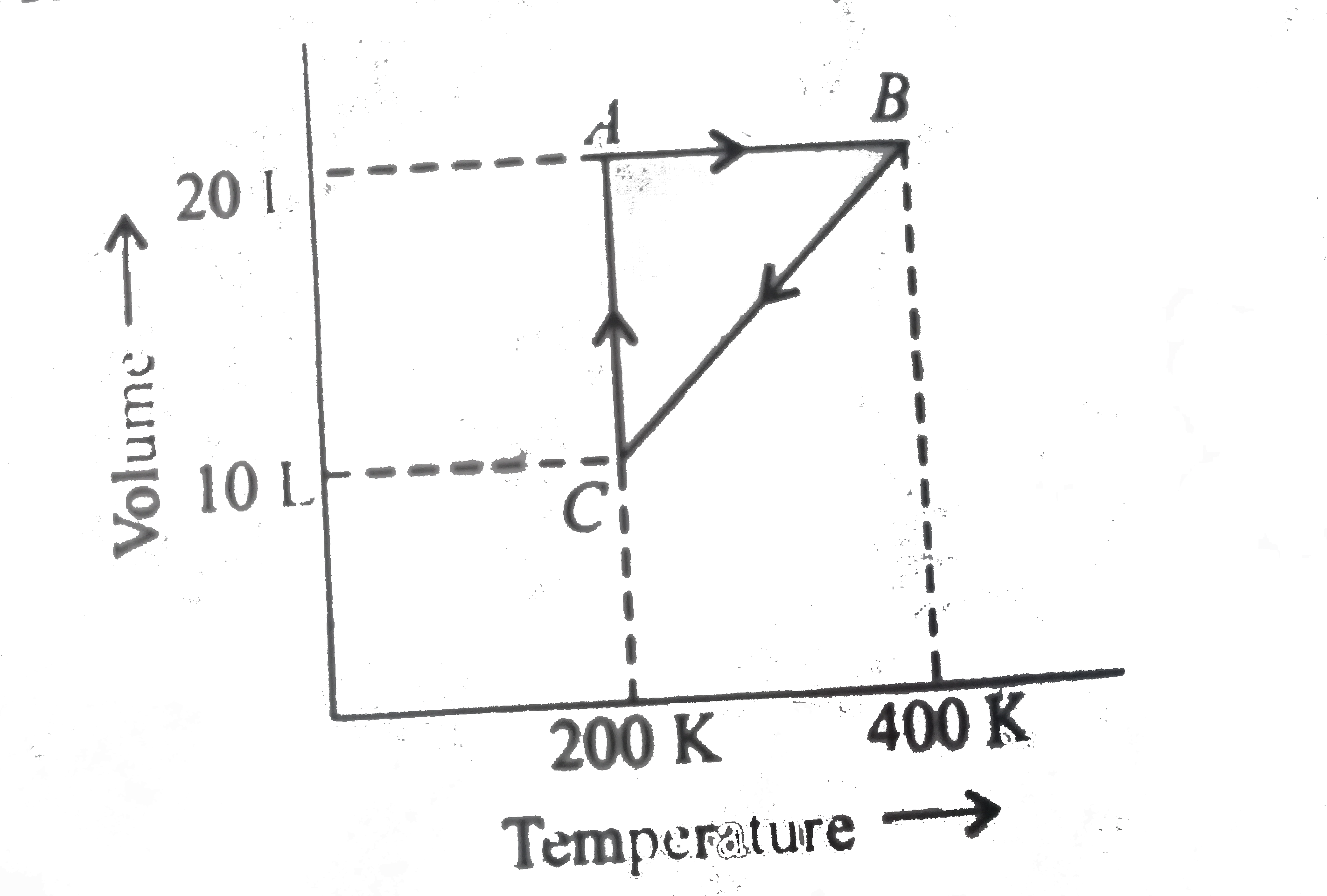
Process A→B representsView SolutionA gas is taken through the cycle A→B→C→A, as shown in figure, what is the net work done by the gas?
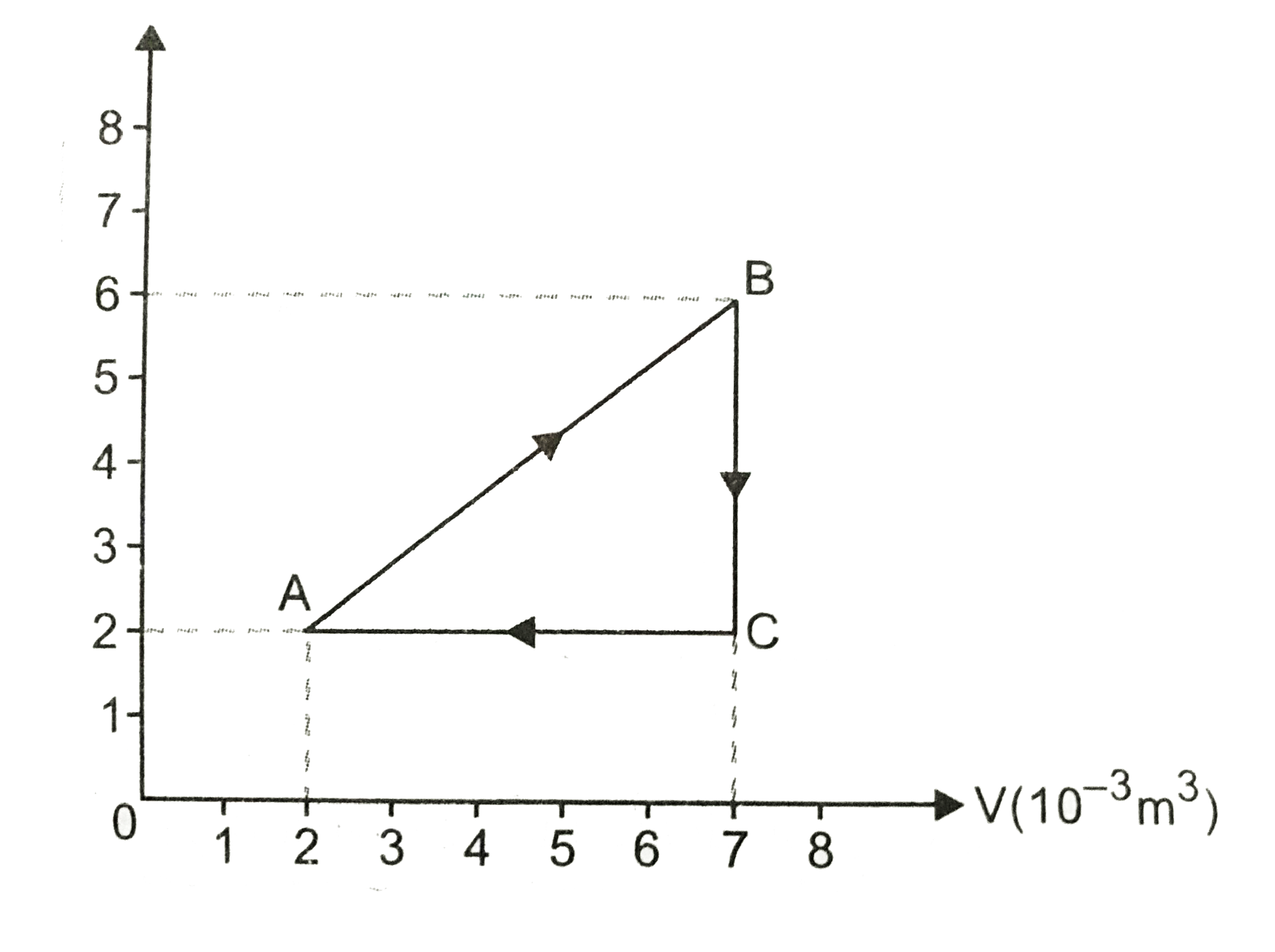 View Solution
View SolutionIsobaric expansion from A→B, isochoric pressure drop from B→C, isothermal compression C→A.
View SolutionIsothermal expansion from A→B, isochoric pressure increase from B→C, isobaric compression from C→D, isochoric pressure drop from D→A.
View SolutionAn ideal gas is taken through the cycle A→B→C→A, as shown in figure. If the net heat supplied to the gas in the cycle is 5 J the work done by the gas in the process A→B is
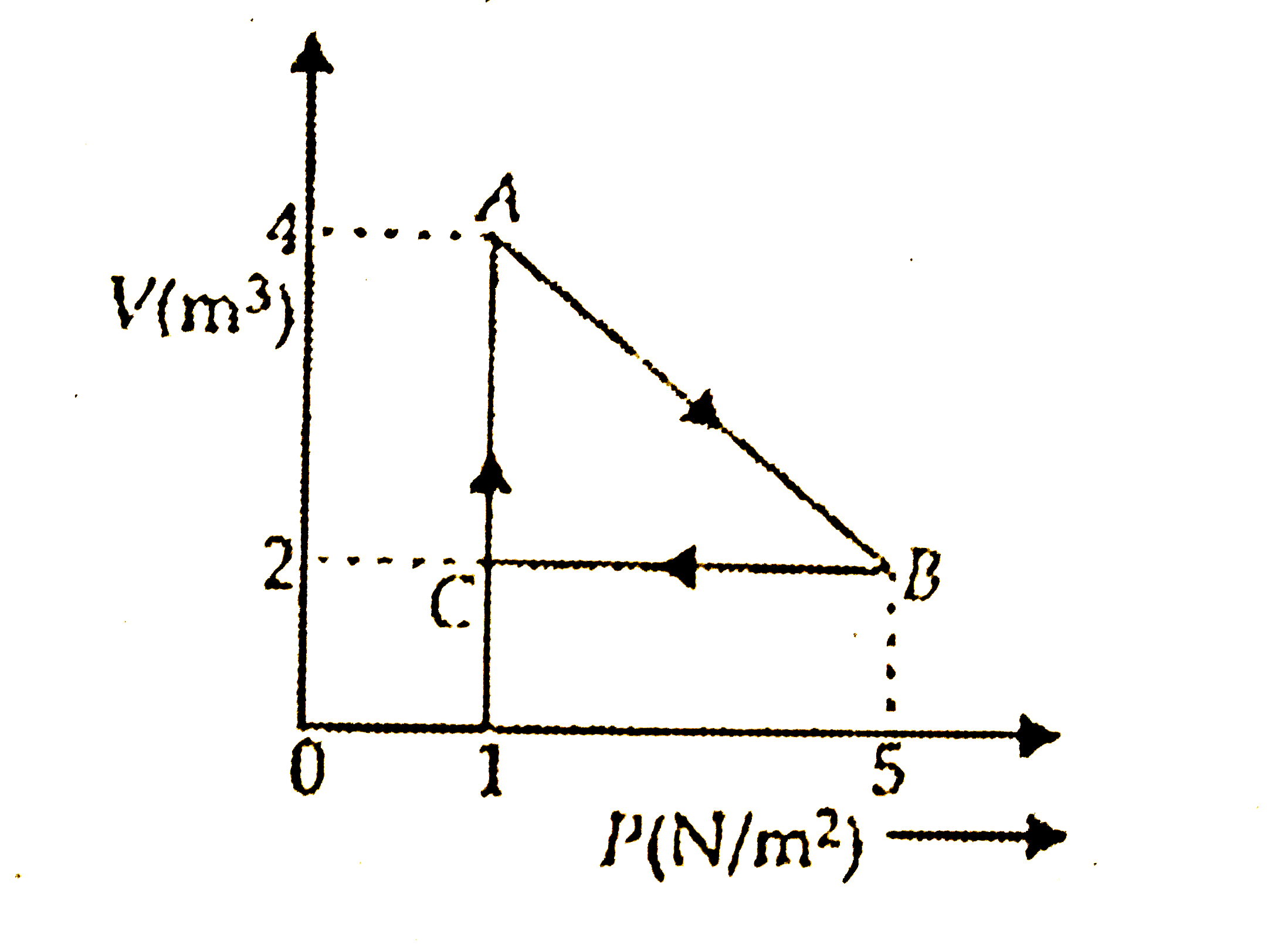 View Solution
View SolutionFill in the blanks A and B
Kingdom → Phylum → [A] → Order → [B]View SolutionOn mole of a monoatomic ideal gas is taken through the cycle shown in figure .
A→B : Adiabatic expansion B→C : Cooling at constant volume
C→D: Adiabatic compression D→A : Heating at constant volume
The pressure and temperature at A,B, etc, are denoted by PA,TA,PB,TB etc., respectively . Given that TA=1000K,PB=(23)PAandPC=(13)PA. Calculate the following quantities: (i) The work done by the gas in the processs A→B (ii) The heat lost by the gas in the process B→C (iii) The temperature TD.(Given:(23)2/5=0.85)
< View Solution
View SolutionIn the decay process:
A−α−−→B−β−−→C−β−−→DView Solution

