A system undergoes a cyclic process in which it absorbs Q, heat and gives out Q2. heat. The efficiency of the process is n and the work done is W.
W=Q1−Q2
η=WQ1
η=Q2Q1
η=1−Q2Q1
The correct Answer is:A, B, D
To solve the problem, we need to analyze the cyclic process in thermodynamics where a system absorbs heat Q1, gives out heat Q2, and does work W. We are also given the efficiency η of the process.
1. Understanding the First Law of Thermodynamics:
The first law of thermodynamics states that the change in internal energy of a system is equal to the heat added to the system minus the work done by the system. In a cyclic process, the internal energy returns to its initial state, so the change in internal energy is zero.
ΔU=Q−W=0⟹Q=W
Here, Q is the net heat added to the system.
2. Relating Heat and Work:
Since the system absorbs Q1 and gives out Q2, the work done W can be expressed as:
W=Q1−Q2
This equation shows that the work done by the system is equal to the heat absorbed minus the heat rejected.
3. Calculating Efficiency:
The efficiency η of a cyclic process is defined as the ratio of the work done W to the heat input Q1:
η=WQ1
Substituting the expression for W:
η=Q1−Q2Q1
This can be rearranged to:
η=1−Q2Q1
4. Identifying Correct Relations:
Now, we can summarize the relationships derived:
- Work done: W=Q1−Q2
- Efficiency: η=WQ1 or η=1−Q2Q1
Conclusion:
From the analysis:
- The correct relations are:
- A: W=Q1−Q2 (Correct)
- B: η=WQ1 (Correct)
- C: η=Q2Q1 (Incorrect)
- D: η=1−Q2Q1 (Correct)
Thus, options A, B, and D are correct.
The first law of thermodynamics states that the change in internal energy of a system is equal to the heat added to the system minus the work done by the system. In a cyclic process, the internal energy returns to its initial state, so the change in internal energy is zero.
ΔU=Q−W=0⟹Q=W
Here, Q is the net heat added to the system.
Since the system absorbs Q1 and gives out Q2, the work done W can be expressed as:
W=Q1−Q2
This equation shows that the work done by the system is equal to the heat absorbed minus the heat rejected.
The efficiency η of a cyclic process is defined as the ratio of the work done W to the heat input Q1:
η=WQ1
Substituting the expression for W:
η=Q1−Q2Q1
This can be rearranged to:
η=1−Q2Q1
Now, we can summarize the relationships derived:
- Work done: W=Q1−Q2
- Efficiency: η=WQ1 or η=1−Q2Q1
From the analysis:
- The correct relations are:
- A: W=Q1−Q2 (Correct)
- B: η=WQ1 (Correct)
- C: η=Q2Q1 (Incorrect)
- D: η=1−Q2Q1 (Correct)
Topper's Solved these Questions
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - COMPREHENSIONS-I
3 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - COMPREHENSIONS-II
2 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) (LEVEL-I) (ASSERTION AND REASON)
2 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question
2 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - NUMERICAL BASED QUESTIONS DECIMAL TYPE
5 Videos
Similar Questions
A system works in a cyclic process. It absorbs 20 calories of heat and rejects 60J of heat during the process. The magnitude of work done (J) is [1calorie=4.2J]:
View SolutionA heat engine undergoes a process in which its intemal energy decreases by 400 J and it gives out 150 J of heat. During the process
View Solution
Knowledge Check
A system undergoes a cyclic process in which it absorbs Q1 heat and gives out Q2 heat. The efficiency of the process is η and work done is W. Select correct statement:
AW=Q1−Q2Bη=WQ1Cη=Q2Q1Dη=1−Q2Q1A system undergoes a cyclic process in which it absorbs heat Q1 and gives away heat Q2. If the efficiency of the process is η and the work done is W, then
AW=Q1−Q2Bη=WQ1Cη=Q2Q1Dη=1−Q2Q1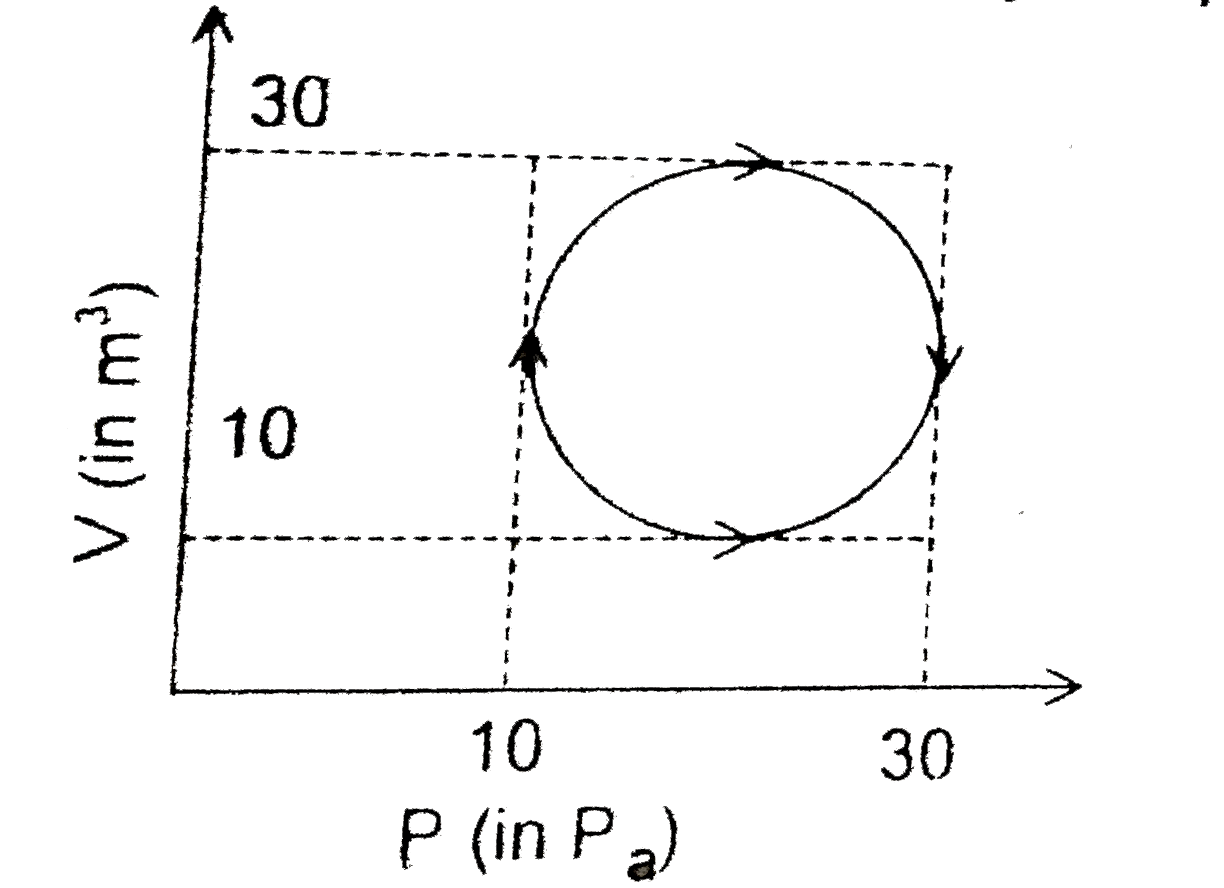
A system works under cyclic process as follow
Heat absorbed during the process isA227×102JB227×103JC227×104JD227×105J
Work Done In Cyclic Process
View Solution
An ideal gas undergoes a cyclic process, in which one process is isochoric, one process is isothermal and one process is adiabatic. During the isothermal process, 40 J heat is released by the gas, and during the isochoric process, 80 J heat is absorbed by the gas. if work done by the gas during adiabatic process is W1 and during isothermal process is W2 then the magnitude of W1W2 will be equal to:
View SolutionIn a cyclic process, work done by the system is
View SolutionIn a cyclic process, work done by the system is
View SolutionA system absorbs 640 J heat and does work. The change in internal energy (ΔU) for the process is 380 J. The work done by the system is __ J
View Solution
