The molar heat capacity for an ideal gas
is zero for an adiabatic process
is infinite for an isothermal process
depends only on the nature of the gas for a process in which either volume or pressure is constant
is equal to the product of the molecular weight and specific heat capacity for any process
The correct Answer is:A, B, C, D
Step by step video, text & image solution for The molar heat capacity for an ideal gas by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - COMPREHENSIONS-I
3 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - COMPREHENSIONS-II
2 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) (LEVEL-I) (ASSERTION AND REASON)
2 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question
2 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - NUMERICAL BASED QUESTIONS DECIMAL TYPE
5 Videos
Similar Questions
The molar heat capacity of an ideal gas (γ=1.40) varies during a process according to the law C=20.0+500T.
Is the process polytropic ?
View SolutionThe molar heat capacity of an ideal gas (γ=1.40) varies during a process according to the law C=20.0+500T.
Find the work done by a mole of the gas when heated from T1=200 K to T2=544 K .
View Solution
Knowledge Check
The molar heat capacity of an ideal gas in a process varies as C=CV+αT2 (where CV is mola heat capacity at constant volume and α is a constant). Then the equation of the process is
AVe−(αT22R)= ConstantBVe−(αT2R)= constantCVe−(2αT2R)= constantDVe−(3αT22R)= constantThe molar heat capacity C for an ideal gas going through a given process is given by C=aT, where 'a' is a constant. If γ=CpCv, the work done by one mole of gas during heating from T0 to ηT0 through the given process will be
A1alnηBalnη−(η−1γ−1)RT0Calnη−(γ−1)RT0Dnone of theseFor certain process the molar heat capacity of an ideal gas is found to be (Cv+R2) , where Cv is the molar heat capacity of the same gas at constant volume. For the given process, it can be concluded that
APV=constantBPV = constantCV2P = constantDNone of these
Find the value of molar heat capacity for an ideal gas in an adiabatic process.
View SolutionFind the molar heat capacity of an ideal gas with adiabatic exponent γ for the polytorpic process PVn= Constant.
View SolutionWhich of the following is true for the molar heat capacity of an ideal gas?
1.It cannot be negative
2.It has only two values (CPandCV)
3.It can have any value
4.It cannot be zero
View SolutionThe molar heat capacity for an ideal monatomic gas is 3R.If dQ is the heat supplied to the gas and dU is the change in its internal energy then for the process the ratio of work done by the gas and heat supplied is equal to
View SolutionDetermine the average molar heat capacity of an ideal gas under going a process shown in fig.
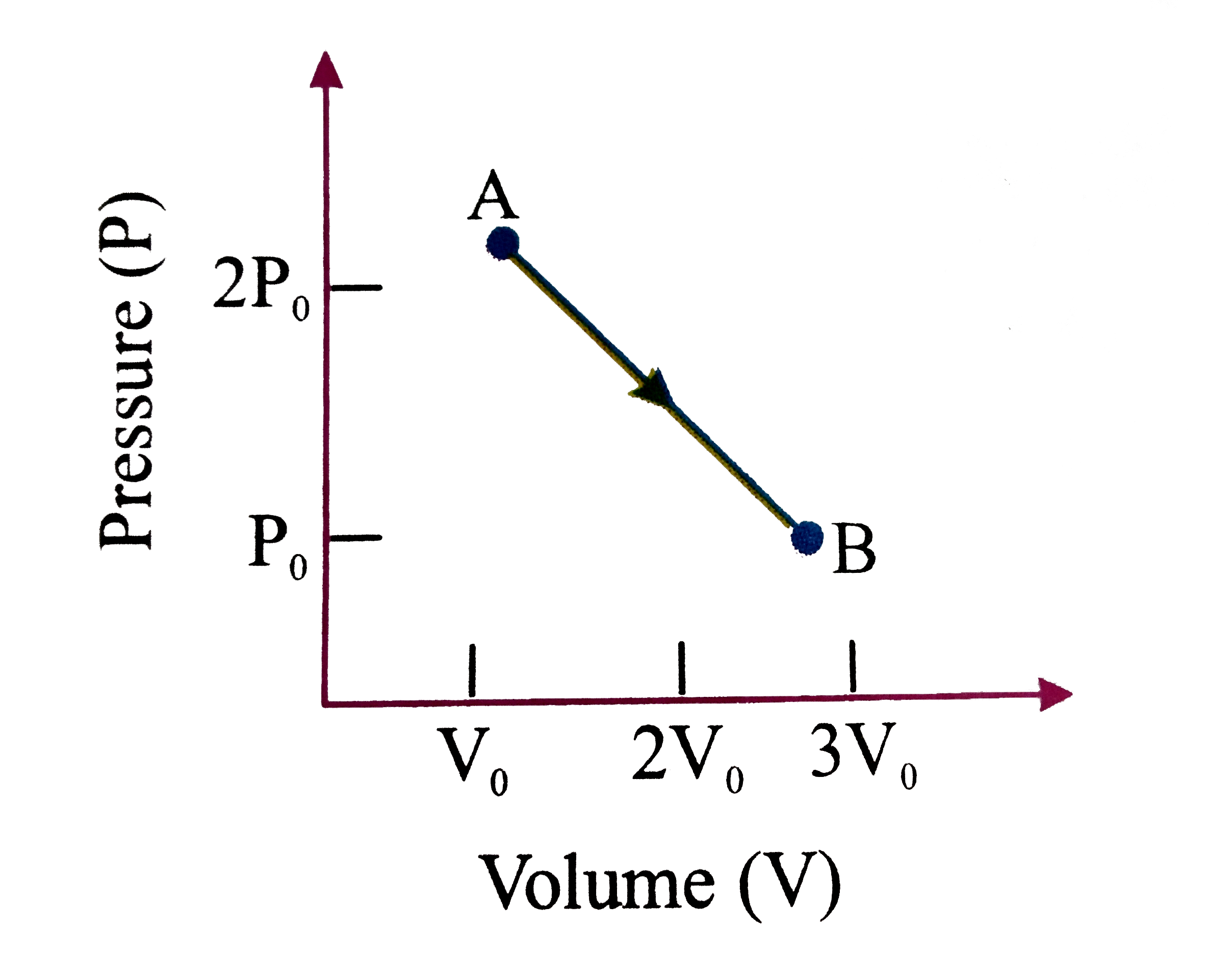
View Solution
