A bar magnet oscillates with a frequency of 10 oscillations per minute . When another bar magnet is placed on its axis at a small distance , it oscillates at 14 oscillations per minute . Now , the second bar magnet is turned so that poles are instantaneous , keeping the location same . The new frequency of oscillation will be
2 vibrations/min
4 vibrations/min
10 vibrations/min
14 vibrations/min
The correct Answer is:A
To solve the problem step by step, we need to analyze the situation of the two bar magnets and how their interaction affects the frequency of oscillation.
Step 1: Understand the initial conditions
The first bar magnet oscillates with a frequency of 10 oscillations per minute (F1 = 10 oscillations/min).
Step 2: Convert frequency to time period
The time period (T1) is the reciprocal of frequency:
T1=1F1=110 oscillations/min
To convert this to seconds, we note that 1 minute = 60 seconds:
T1=60 seconds10=6 seconds
Step 3: Analyze the effect of the second bar magnet
When the second bar magnet is placed on the axis of the first one, the frequency increases to 14 oscillations per minute (F2 = 14 oscillations/min).
Step 4: Convert the new frequency to time period
The time period (T2) is:
T2=1F2=114 oscillations/min
Converting this to seconds:
T2=60 seconds14≈4.29 seconds
Step 5: Relate time periods and magnetic fields
The time period of oscillation of a magnet in a magnetic field is given by:
T∝1√B
Thus, we can write the ratio of the time periods in terms of the magnetic fields:
T1T2=√B2B1
Where B1 is the magnetic field due to the Earth's magnetic field and B2 is the combined magnetic field when the second magnet is placed.
Step 6: Substitute the time periods
Substituting the values we found:
64.29=√BH+BBH
Squaring both sides gives:
(64.29)2=BH+BBH
Let x=BBH:
(64.29)2=1+x
Step 7: Solve for x
Calculating (64.29)2:
(64.29)2≈1.67
Thus,
1.67=1+x⟹x≈0.67
This means:
BBH≈0.67⟹B≈0.67BH
Step 8: Determine the new frequency when the second magnet's poles are reversed
When the second magnet's poles are reversed, the magnetic field becomes BH−B:
B3=BH−B=BH−0.67BH=0.33BH
Step 9: Relate the new time period to the original
Using the relationship:
T3T1=√B1B3
Substituting B1 and B3:
T36=√BH0.33BH=√10.33
Calculating gives:
T3=6√3≈10.39 seconds
Step 10: Calculate the new frequency
The new frequency F3 is:
F3=1T3≈110.39 oscillations/seconds
Converting to oscillations per minute:
F3≈6010.39≈5.77 oscillations/min
Final Answer
The new frequency of oscillation will be approximately 5.77 oscillations per minute.
The first bar magnet oscillates with a frequency of 10 oscillations per minute (F1 = 10 oscillations/min).
The time period (T1) is the reciprocal of frequency:
T1=1F1=110 oscillations/min
To convert this to seconds, we note that 1 minute = 60 seconds:
T1=60 seconds10=6 seconds
When the second bar magnet is placed on the axis of the first one, the frequency increases to 14 oscillations per minute (F2 = 14 oscillations/min).
The time period (T2) is:
T2=1F2=114 oscillations/min
Converting this to seconds:
T2=60 seconds14≈4.29 seconds
The time period of oscillation of a magnet in a magnetic field is given by:
T∝1√B
Thus, we can write the ratio of the time periods in terms of the magnetic fields:
T1T2=√B2B1
Where B1 is the magnetic field due to the Earth's magnetic field and B2 is the combined magnetic field when the second magnet is placed.
Substituting the values we found:
64.29=√BH+BBH
Squaring both sides gives:
(64.29)2=BH+BBH
Let x=BBH:
(64.29)2=1+x
Calculating (64.29)2:
(64.29)2≈1.67
Thus,
1.67=1+x⟹x≈0.67
This means:
BBH≈0.67⟹B≈0.67BH
When the second magnet's poles are reversed, the magnetic field becomes BH−B:
B3=BH−B=BH−0.67BH=0.33BH
Using the relationship:
T3T1=√B1B3
Substituting B1 and B3:
T36=√BH0.33BH=√10.33
Calculating gives:
T3=6√3≈10.39 seconds
The new frequency F3 is:
F3=1T3≈110.39 oscillations/seconds
Converting to oscillations per minute:
F3≈6010.39≈5.77 oscillations/min
The new frequency of oscillation will be approximately 5.77 oscillations per minute.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - MAGNETISM AND MATTEREXERCISE - EXERICSE4videos
MAGNETISM AND MATTER
- BOOK - FIITJEECHAPTER - MAGNETISM AND MATTEREXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE ) (LEVEL -1)18videos
MAGNETISM AND MATTER
- BOOK - FIITJEECHAPTER - MAGNETISM AND MATTEREXERCISE - SOLVED PROBLEMS OBJECTIVE : (LEVEL - 1)10videos
MAGNETISM AND MATTER
- BOOK - FIITJEECHAPTER - MAGNETISMEXERCISE - Example12videos
MAGNETISM
- BOOK - FIITJEECHAPTER - MODERN PHYSICSEXERCISE - Numerical based questions5videos
MODERN PHYSICS
Similar Questions
Knowledge Check
- Question 1 - Select One
The magnetic needle of an oscillation magnetometer makes 10 oscillations per minut under the action of earth's magnetic field along. When a bar magnet is placed at some distance along the axis of the needle it makes 14 oscillations per minute. If the bar magnet is turned so that its poles interchange their position, then the new frequency of oscillation of the needle is:
A10 vibrations per minuteB14 vibrations per minuteC4 vibrations per minuteD2 vibration per minute - Question 2 - Select One
At a place where angle of dip is 45∘, a magnet oscillates with 30 oscillations per minute. At another place where angle of dip is 60∘, the same magnet makes 20 oscillations per minute The ratio of total magnetic fields at the two places is
A3√2:2B9:4C4:9D9√2:4 - Question 3 - Select One
A magnetic needle has a frequency of 20 oscillations per minute in the earth's horizontal field. When the field of a manget supports the earths horizontal field, the frequency increases to 30 oscillations per minute. The ration of the field of the magnet to that of the earth is
A4:7B7:4C5:4D4:5
The frequency of oscillation of the magnet in an oscillation magnetometer in the earth's magnetic field is 40 oscillations per minute. A short bar magnet is placed to the north of the magnetometer, at a separation of 20cm from the oscillating magnet, with its north pole pointing towards north (figure). The frequency of oscillation is found to increase to 60 oscillations per minute. Calculate the magnetic moment of this short bar magnet. Horizonatl component of the earth's magnetic field is 24μT.
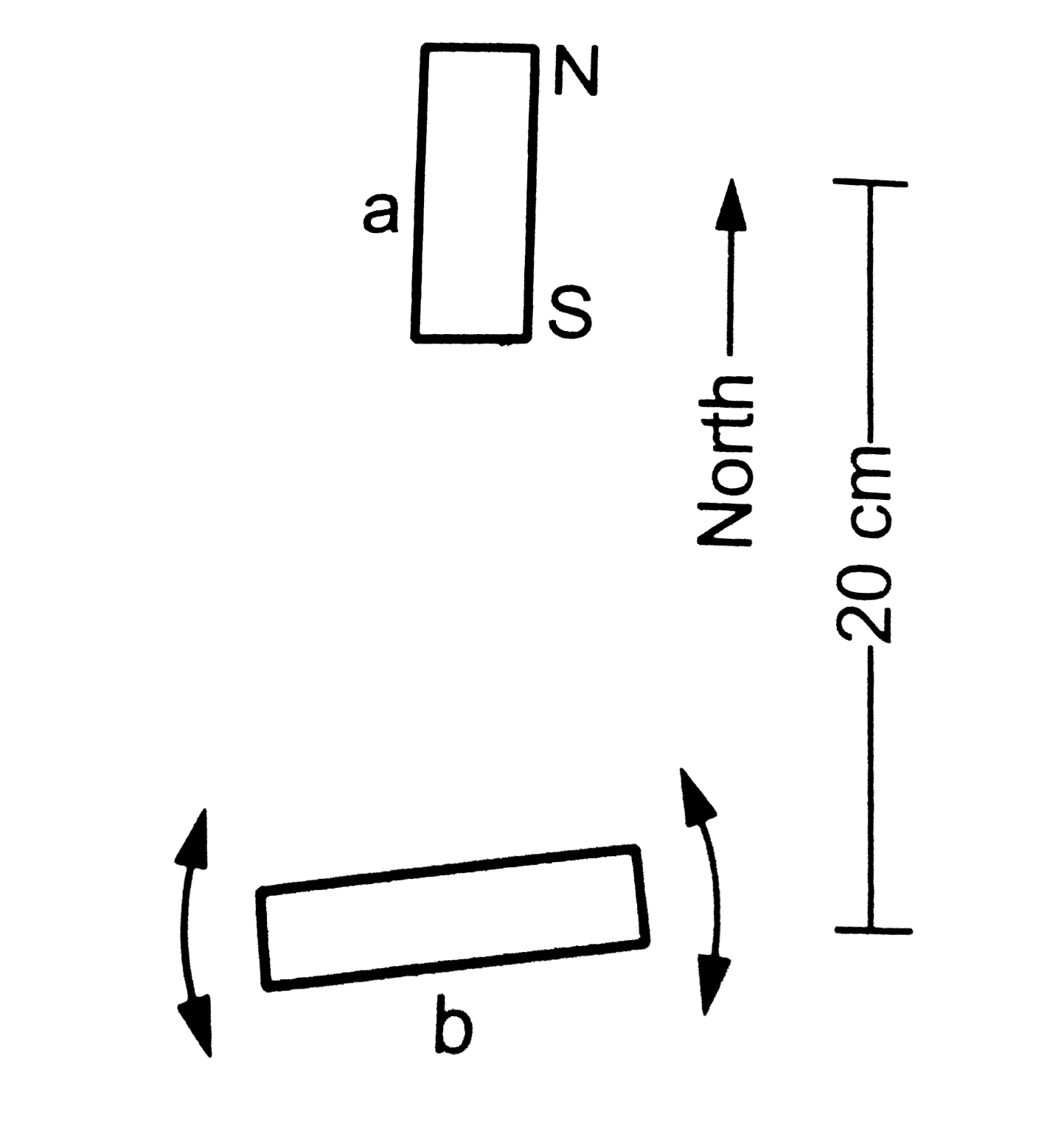 View Solution
View SolutionA bar magnet suspended at a place P where dip angle is 60∘ gives 10 oscillations per minute. The same bar magnet suspended at another place Q where dip angle is 30∘ gives 20 oscillations per minute. The ratio of magnetic fields at P and Q,BPBOis
View SolutionA frequency of 1 Hz means _________ oscillations per second.
View SolutionA small magnetic needle performs 10 oscillations/minute in the earth's horizontal magnetic field . When a bar magnet is placed near the small magnet in same position , frequency of oscillations becomes 10√2 oscillations/minute . If the bar magnet be turned around end to end , the rate of oscillation of small magnet will become
View SolutionAt a certain place a small bar magnet completes 30 oscillations per minute. At another place, where the magnetic field is double, its time period will be
View Solution

