Two circular loops of radii R and r (R > > r) have same cenre and carry currents I and i respectively. Find the maximum torque and maximum angular acceleration of smallar loop, if it is free to rotate about y axis where as the bigger loop is fixed. (Neglect the inductance of the system). The mas of the smaller loop is m.

The magnetic induction due to larger current loop at the centre O is
B=μ0I2R
The magnetic moment of the smaller loop =μ=(πr2)i
implie The maximum torque experienced by the smaller loop
=τ=μB=(πr2i)(μ0I2R)=μ0Iir2π2R
⇒ The maximum angular accleration of the smallar loop
=α=τ1, (moment of inerta I=mr2/2∴ rotation is about diameter)
⇒α=μIir22Rmr22=μ0IimR
Topper's Solved these Questions
- MAGNETICBOOK - FIITJEECHAPTER - MAGNETICEXERCISE - Solved Problems (Objective)
14 Videos
- MAGNETICBOOK - FIITJEECHAPTER - MAGNETICEXERCISE - Comprehension-1
3 Videos
- MAGNETICBOOK - FIITJEECHAPTER - MAGNETICEXERCISE - Numerical Based Type
2 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
- MAGNETISMBOOK - FIITJEECHAPTER - MAGNETISMEXERCISE - Example
12 Videos
Similar Questions
Two coaxial circular loops of raadii r1 and r2 are separated by a distance x and carry currents i1 and i2 respectively. Calculate the mutual inductance. What is the force between the loops ?
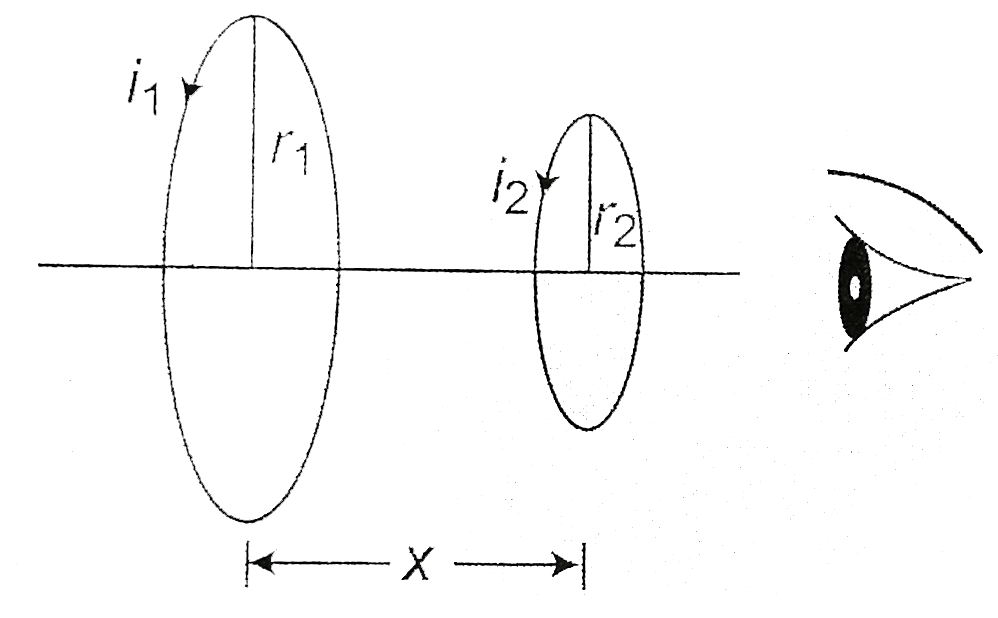
View SolutionTwo circular loops A and B of radii R and 4R are kept concentrically in the same plane. The loops carry currents I1 and I2 respectively. If the magnetic field at a point on the common axis of the loops at a distance 2R from their common centre is zero, the ratio I1I2 is _________.
View Solution
Knowledge Check
Two concentric co - planar circular loops of radius R and r(<<R) are placed as shown in the figure. The mutual inductance of the system will be
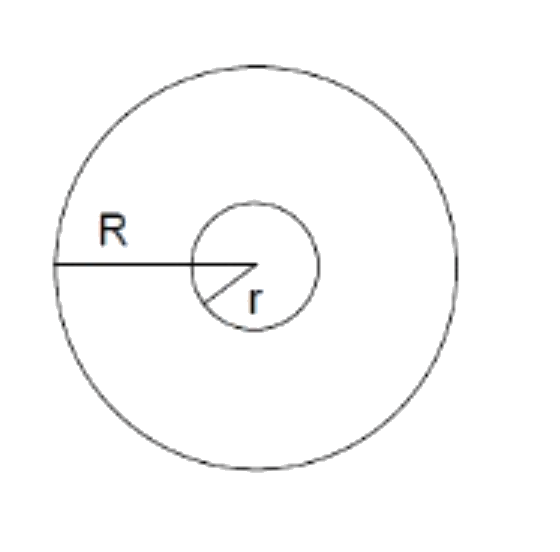 Aπμ0r22RBπμ0r24RCπμ0R24rDπμ0R22r
Aπμ0r22RBπμ0r24RCπμ0R24rDπμ0R22rA very small circular loop of radius a is initially coplanar & concentric with a much larger circular loop of radius b (>>a). A constant current is passed in the large loop which is kept fixed in space & the small loop is rotated with angular velocity omega about a diameter. The resistance of the small loop is R & its self inductance is negligible. The current in the larger loop is clockwise.
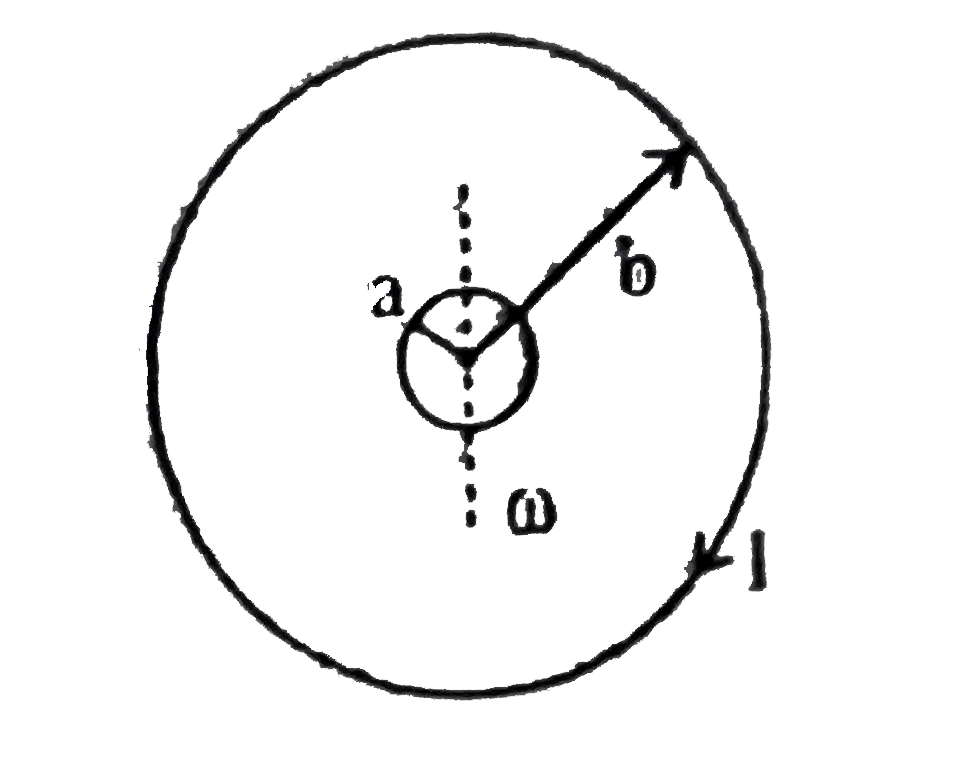
Calculate how much torque must be exerted on the small loop to rotate it.AωR(πb2μ0Isinωt2b)2BωR(πb2μ0I2b)2sinωtcosωtCωR(πa2μ0Isinωt2b)2DNone of theseA very small circular loop of radius a is initially coplanar & concentric with a much larger circular loop of radius b (>>a). A constant current is passed in the large loop which is kept fixed in space & the small loop is rotated with angular velocity omega about a diameter. The resistance of the small loop is R & its self inductance is negligible. The current in the larger loop is clockwise.
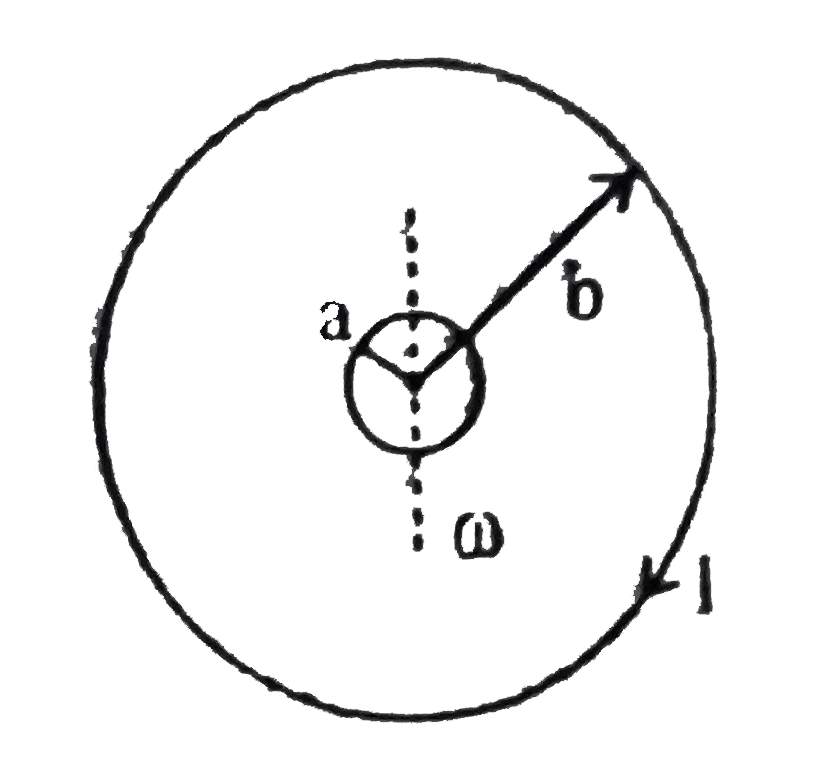
Find the current in the small loop as a function of time.Aπa2μ0Iωsinωt2bRBπa2μ0Iωcosωt2bRCπb2μ0Iωsinωt2aRDπb2μ0Iωcosωt2aR
A very small circular loop of radius r is initially coplanar and concentric with a much larger circular loop of radius R(>>r) . A constant current i is passed in the larger loop which is kept fixed in space and the small loop is rotated with angular velocity ω about a diameter. The resistance of the small loop is R0 and the inductance is negligible.
(a) Find the current in the small loop as a function of time.
(b) Calculate how much troque must be exerted on the small loop to rotate it.
View SolutionIn the figure shown two loops ABCD &EFGH are in the same plane. The smaller loop carries time varying current I=bt, where b is a positive constant and t is time. The resistance of the smaller loop is r and that of the larger loop is R : (Neglect the self inductance of large loop ). The magnetic force on the loop EFGH due to loop ABCD is μ20Iabxπ2Rln43 . Find the value of x.
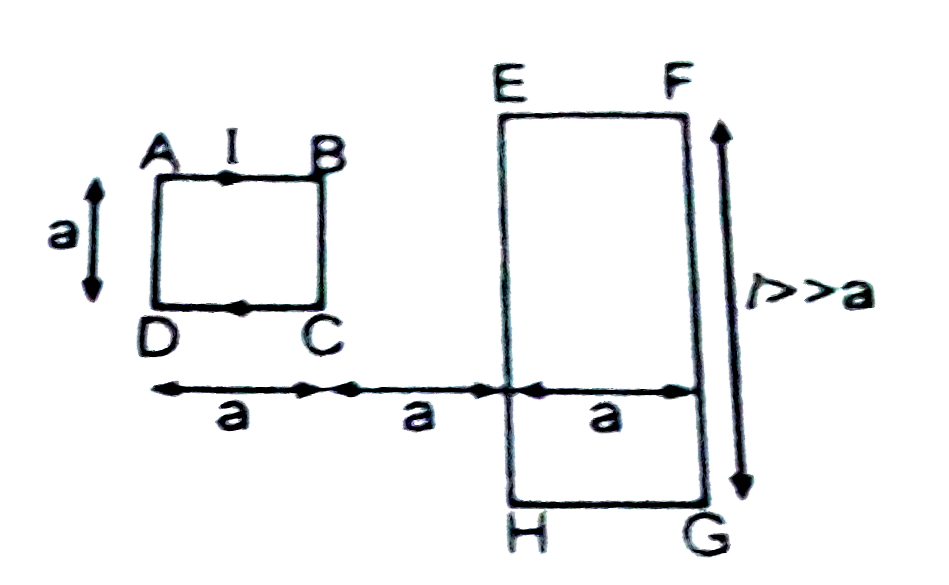
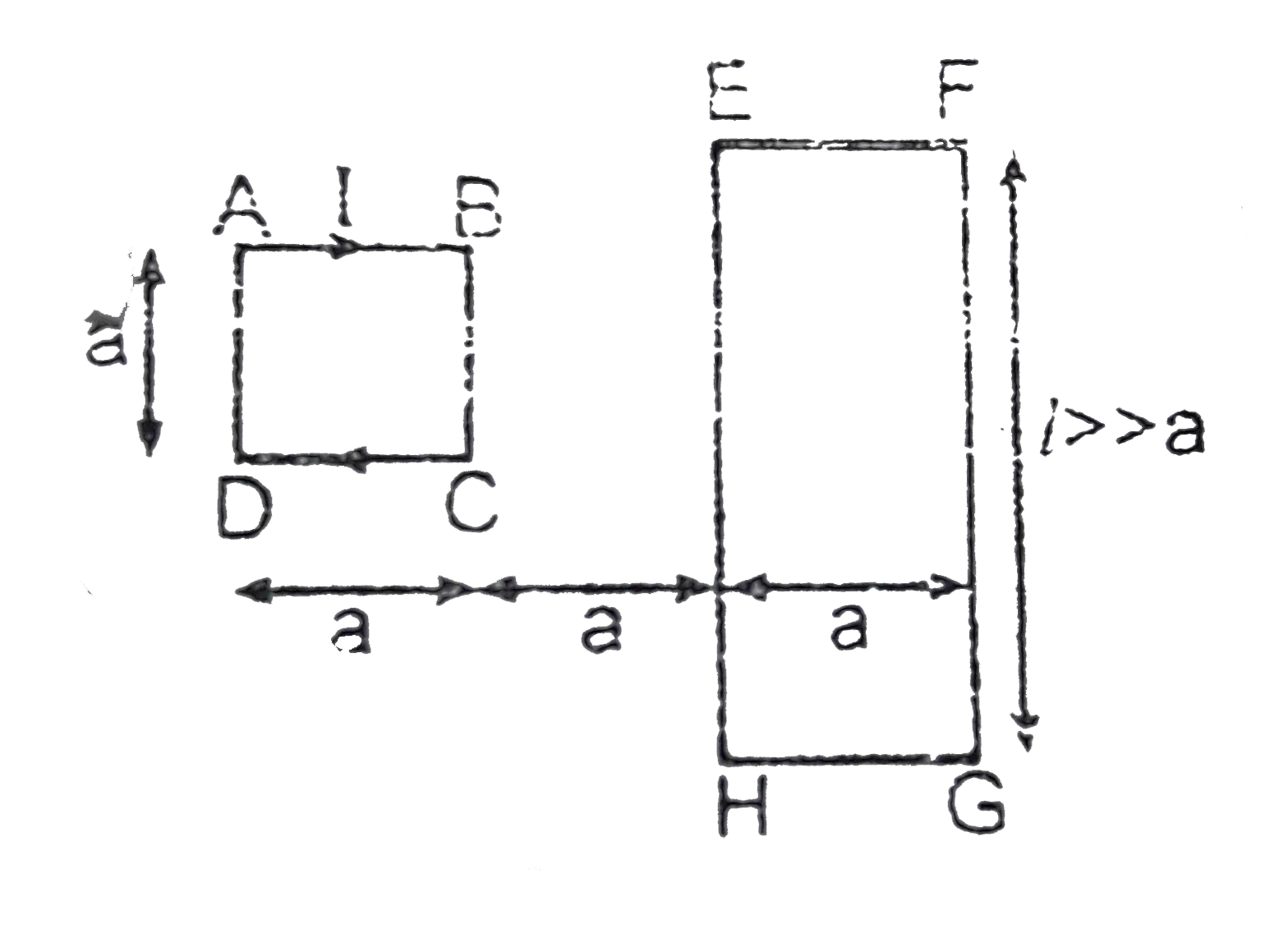
View SolutionIn the figure shown two loops ABCD & EFGH are in the same plane.The smaller loop carries time varying current I=bt, where b is a positive constant and t is time.The resistance of the smalller loop is r and that of the larger loop is R.:(Neglect the self inductance of large loop)
The magnetic force on the loop EFGH due to loop ABCD is μ20Iabxπ2Rln43.Findout value of x.
View SolutionFind mutual inductance if we have a square loop of side r instead of a small circular loop of side r at the centre of bigger circular loop.
View SolutionTwo concentric coplanar circular conducting loops have radii R and r(R>>r) .Their mutual inductance is proportional to
View Solution
