To know the surface of matter on smallest scale we allow an energetic charged particle to slam into a solid target or allow two energetic charged particle to collide head on. We use cyclotrons to give very high kinetic energy to the charged particles, we arrange for the proton to circulate in a magnetic field and give it a modest electrical kick once per revolution. Two hollow D shaped objects, called does are part of an electrical oscillator that alternates the electric potential difference across the gap between the does back ad forth. the does are immersed in a magnetic field whose direction is out of the plane of page and that is set up by a large electromagnet, suppose a proton injected by a source S at the centre of the cyclotron, initially moves towards a negatively charged de. It will accelerate toward this doe and enter it. Once inside, it is shielded from electric fields by the copper walls of the dee: that is the electric field does not enter the dee. The magnetic field however is not screened by the copper dee. So, the proton moves in a circular path whose radius, which depends on speed is given by r=mvqB
The key to the operation of cyclotron is that the frequency f at which the proton circulates in the field and thaat does not depend on its speed must be equal to the fixed frequency Foce of the electrical oscillator. The resonance condition is given by
qB=2πmFoce
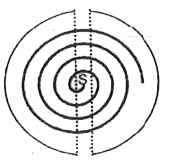
If a proton circulates 200 times in a magnetic field of 1.5 T and receives an energy boost of 100 keV every time it completes an orbit it will end up with a kinetic energy of
100 KeV
20 MeV
40 MeV
20 MeV
The correct Answer is:B
Topper's Solved these Questions
- MAGNETICBOOK - FIITJEECHAPTER - MAGNETICEXERCISE - Comprehension -3
3 Videos
- MAGNETICBOOK - FIITJEECHAPTER - MAGNETICEXERCISE - Comprehension -4
2 Videos
- MAGNETICBOOK - FIITJEECHAPTER - MAGNETICEXERCISE - Comprehension -1
3 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
- MAGNETISMBOOK - FIITJEECHAPTER - MAGNETISMEXERCISE - Example
12 Videos
Similar Questions
The basic principle underlying the hall effect is the Lorentz force. Whenk an electron moves along a direction perpendicular to an applied magnetic field. It exeriences a force acting normal to both the directions and moves in response to this force and the force exerted by the internal electric field. For an - n-type bar shaped semiconductor, the carries are predominatly electrons of bulk density n. We assume that the constant current I flows along the x-axis from left to right in the presence of a magnetic field toward the negative z-axis resulting in an excess surface electrical charge on the sides of the sample. this charge results in the hall voltage a potential drop across the two sides of the sample
Thre transverse voltage is the hall voltage VH and its magnitude is equal to IB/qnD, where I is the current B is the magnetic field, d is the sample thickness and q is the elementary charge. A silver ribbon lies as shown in the adjacent figure (z1=11.8mm and = 0.23 mm) carrying a current of 120 A in the x -direction in unifrom magnetic field B = 0.95 T. If electron density is 5.85×1028/m3 then
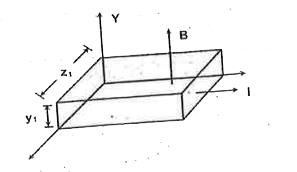
magnitude of the drift velocity of electron is
View SolutionA 100 turn closely wound circular coil of radius 10 cm carries a current of 3.2A. A uniform horizontal magnetic field of strength 2T is turned on. The axis of the coil is initially in the direction of the field . The coil rotates through an angle of 90∘ under the influence of the magnetic field. The moment of inertia of the coil is 0.1 kg m2
What is the field at the centre of the coil?
View SolutionAnalog voltmeters and ammeters work b measuring the torque exerted by a megentic field on a current carrying coil. The reading is displayed by means of the deflection of a pointer over a scale. The adjacent figure shows the essentials of a galvanometer, on which both analog ammters and analog voltmeters are based. Assume that the coil is 2.1 cm high, 1.2 cm wide has 250 turns and is mounted so that it can rotate about an axis (into the page) in a uniform radial magnetic field with B = 0.23 T. for any orientation of the coil, the net magnetic field through the coil is perpendicular to the normal vector of the coil (and thus parallel to the plane of coil) A spring SP provides a counter torque that balance the magnetic torque so that a given steady current I in the coil results in a steady angular diflection ϕ. The greater the current is greater the deflection is and thus greater the torque required of the spring is A current of 100 μA produces an angular deflection of 28∘.
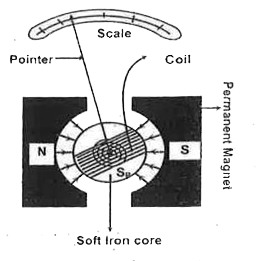
What must be the torional conctant k of the spring ?
View SolutionGenerally, we consider that during slowing of a moving automobile, its retardation is constant, but in practice this is seldom the case. Under many circumstances, especially at high speed, we usually apply the brakes slowly at first and then more strongly as the car slows. The braking force therefore depends on the time during the interval over which the car is slowing and acceleration changes with time.
ax(t)=vA−vxdt=Fx(t)m
∫vxv0xdVx=∫10Fx(t)mdt
∴Vx=V0x+1m∫10Fx(t)dt
x(t)=x0+∫10Vx(t)dt
An example for the same is discussed here.
A car of mass m = 1000 kg is moving with 25 m/s. The driver begins to apply the brakes so that the magnitude of the braking force increases linearly with time at a rate of 2000 N/s.
Read the above passage carefully and answer the following questions.
Find the velocity of the car at t = 10 sec.
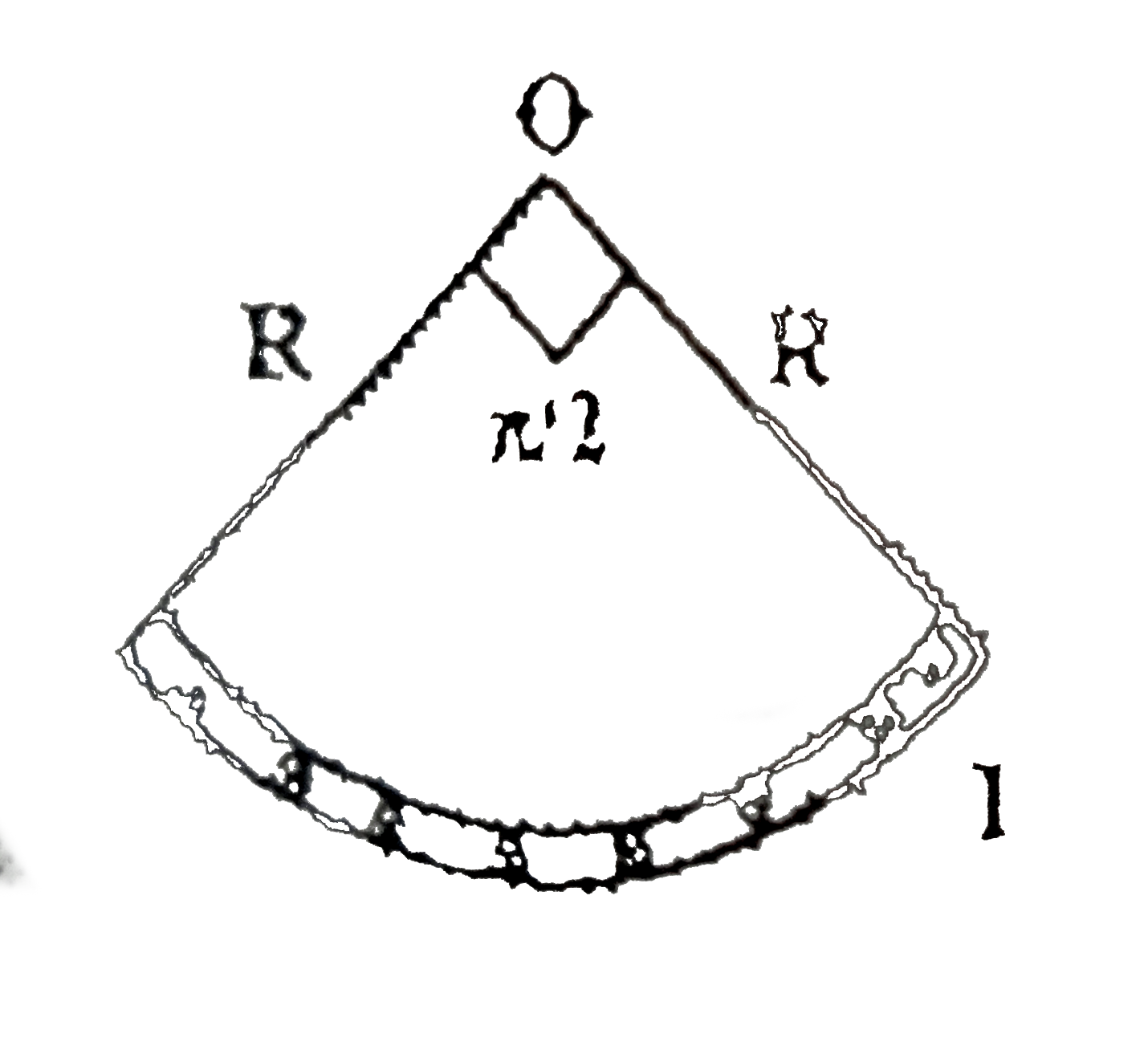
View SolutionA current I flows in a long straight wire (into the plane of the paper) with cross-section having the from of a circular are of radius R a shown in the figure. Find the magnetic induction at the point O.
View SolutionIn a cyclotron the radius of dees is R and the applied magnetic field has a magnitude of B. Particles having charge q and mass m are accelerated using this cyclotron and the maximum kinetic energy that can be imparted to a particle is k. (a) Find k in terms of R, B, q and m. (b) If protons and alpha particles are accelerated using this cyclotron which particle (proton or alpha) will gain more kinetic energy? (c) Can we use a cyclotron to impart very high kinetic energy to an electron?
View SolutionThe cyclotron is a device which is used to accelerate charged particles such as protons, deutrons, alpha particles, etc. to very high energy. The principle on which a cyclotron works is based on the fact that an electric field can accelerate a charged particle and a magnetic field can throw it into a circular orbit. A particle of charge +q experiences a force qE in an electric field E and this force is independent of velocity of the particle. The particle is accelerated in the direction of the magnetic field. On the other hand, a magnetic field at right angles to the direction of motion of the particle throws the particle in a circular orbit in which the particle revolves with a frequency that does not depend on its speed. A modest potential difference is used as a sources of electric field. If a charged particle is made to pass through this potential difference a number of times, it will acquire an enormous by large velocity and hence kinetic energy. Which of the following cannot be accelerated in a cyclotron?
View SolutionThe cyclotron is a device which is used to accelerate charged particles such as protons, deutrons, alpha particles, etc. to very high energy. The principle on which a cyclotron works is based on the fact that an electric field can accelerate a charged particle and a magnetic field can throw it into a circular orbit. A particle of charge +q experiences a force qE in an electric field E and this force is independent of velocity of the particle. The particle is accelerated in the direction of the magnetic field. On the other hand, a magnetic field at right angles to the direction of motion of the particle throws the particle in a circular orbit in which the particle revolves with a frequency that does not depend on its speed. A modest potential difference is used as a sources of electric field. If a charged particle is made to pass through this potential difference a number of times, it will acquire an enormous by large velocity and hence kinetic energy.
The working of a cyclotron is based on the fact that
View SolutionThe cyclotron is a device which is used to accelerate charged particles such as protons, deutrons, alpha particles, etc. to very high energy. The principle on which a cyclotron works is based on the fact that an electric field can accelerate a charged particle and a magnetic field can throw it into a circular orbit. A particle of charge +q experiences a force qE in an electric field E and this force is independent of velocity of the particle. The particle is accelerated in the direction of the magnetic field. On the other hand, a magnetic field at right angles to the direction of motion of the particle throws the particle in a circular orbit in which the particle revolves with a frequency that does not depend on its speed. A modest potential difference is used as a sources of electric field. If a charged particle is made to pass through this potential difference a number of times, it will acquire an enormous by large velocity and hence kinetic energy.
Cyclotron is not suitable for accelerating
View SolutionVan de Graff generator is used to produce high energetic charged particles of energy of about
View SolutionGive any three pracitical application of high energetic charged particles obtained in a cyclotron
View SolutionHow do we know the charge of a sol particle?
View SolutionA charged particle having a mass of 1.6xx10^(-26) kg comes out of accelerator tube with kinetic energy 2xx10^3 eV . Calculate the smallest magnitude of the magnetic field that should be applied in vertically downwards direction to just prevent the charged particle from colliding the plate (Assume charge on particle = charge of the proton)
View Solutionदो आवेशित कण को जिनके द्रव्यमान 4m एवं m और आवेश +q एवं + 3q हैं, एक समान विद्युत क्षेत्र में रखा है। यदि इसे 2 सेकण्ड तक गति करने दिया जाए तो दोनों कणों की गतिज ऊर्जाओं का अनुपात होगा
View SolutionTo know the surface of matter on smallest scale we allow an energetic charged particle to slam into a solid target or allow two energetic charged particle to collide head on. We use cyclotrons to give very high kinetic energy to the charged particles, we arrange for the proton to circulate in a magnetic field and give it a modest electrical kick once per revolution. Two hollow D shaped objects, called does are part of an electrical oscillator that alternates the electric potential difference across the gap between the does back ad forth. the does are immersed in a magnetic field whose direction is out of the plane of page and that is set up by a large electromagnet, suppose a proton injected by a source S at the centre of the cyclotron, initially moves towards a negatively charged de. It will accelerate toward this doe and enter it. Once inside, it is shielded from electric fields by the copper walls of the dee: that is the electric field does not enter the dee. The magnetic field however is not screened by the copper dee. So, the proton moves in a circular path whose radius, which depends on speed is given by r=mvqB
The key to the operation of cyclotron is that the frequency f at which the proton circulates in the field and thaat does not depend on its speed must be equal to the fixed frequency Foce of the electrical oscillator. The resonance condition is given by
qB=2πmFoce

Suppose a cyclotron is operated at an oscillator frequency of 24 MHz and has a dee of radius 26.5 cm. Then what is the magnitude of the magnetic field needed for deuterons to be accelerated in the cyclotrons?
View Solution
