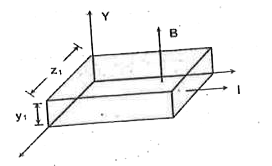
The basic principle underlying the hall effect is the Lorentz force. Whenk an electron moves along a direction perpendicular to an applied magnetic field. It exeriences a force acting normal to both the directions and moves in response to this force and the force exerted by the internal electric field. For an - n-type bar shaped semiconductor, the carries are predominatly electrons of bulk density n. We assume that the constant current I flows along the x-axis from left to right in the presence of a magnetic field toward the negative z-axis resulting in an excess surface electrical charge on the sides of the sample. this charge results in the hall voltage a potential drop across the two sides of the sample
Thre transverse voltage is the hall voltage and its magnitude is equal to IB/qnD, where I is the current B is the magnetic field, d is the sample thickness and q is the elementary charge. A silver ribbon lies as shown in the adjacent figure and = 0.23 mm) carrying a current of 120 A in the x -direction in unifrom magnetic field B = 0.95 T. If electron density is then
magnitude of the drift velocity of electron is
2.35 mm/s
4.7 mm/s
7.5 mm/s
9.4 mm/s
The correct Answer is:B
Topper's Solved these Questions
- MAGNETICBook:FIITJEEChapter:MAGNETICExercise:Comprehension -4
Explore 2 Videos
- MAGNETICBook:FIITJEEChapter:MAGNETICExercise:Numerical Based Type
Explore 2 Videos
- MAGNETICBook:FIITJEEChapter:MAGNETICExercise:Comprehension -2
Explore 3 Videos
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:COMPREHENSION-III
Explore 2 Videos
- MAGNETISMBook:FIITJEEChapter:MAGNETISMExercise:Example
Explore 12 Videos
Similar Questions
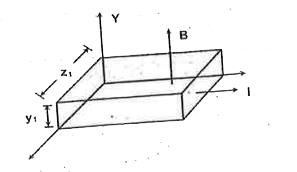
The basic principle underlying the Hall effect is the Lorentz force. When an electron moves along a direction perpendicular to an applied magnetic field, it experiences a force acting normal to both the directions and moves in response to this force and the force exerted by the internal electric field. For an n-type, bar-shaped semiconductor, the carriers are predominantly electrons of bulk density n. We assume that the constant current I flows along the x-axis from left to right in the presence of a magnetic field toward y-axis. Electrons subjected to the lorentz force initially drift away from the current line toward the negative z-axis, resulting in an excess surface electrical charge on the sides of the sample. This charge results in the hall voltage, a potential drop across the two sides of the sample.
The transverse voltage is the hall voltage VH and its magnitude is equal to IB/qnd, where I is the current, B is the magnetic field, d is the sample thickness and q is the elementary charge. A silver ribbon lies as shown in the adjacent figure. (z1=11.8mm and y1=0.23mm) carrying a current of 120A in the x-direction in a uniform magnetic field B=0.95T. If electron density is 5.85×1028/m3, then
What is the value of hall emf ?
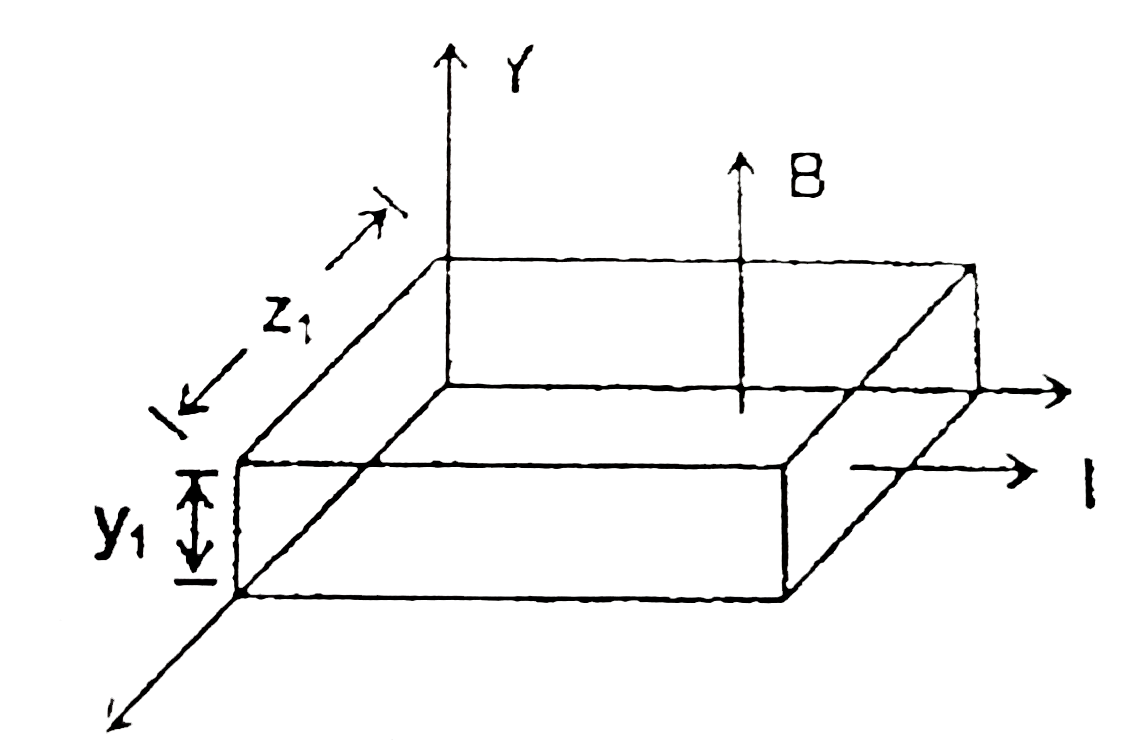
View SolutionThe basic principle underlying the Hall effect is the Lorentz force. When an electron moves along a direction perpendicular to an applied magnetic field, it experiences a force acting normal to both the directions and moves in response to this force and the force exerted by the internal electric field. For an n-type, bar-shaped semiconductor, the carriers are predominantly electrons of bulk density n. We assume that the constant current I flows along the x-axis from left to right in the presence of a magnetic field toward y-axis. Electrons subjected to the lorentz force initially drift away from the current line toward the negative z-axis, resulting in an excess surface electrical charge on the sides of the sample. This charge results in the hall voltage, a potential drop across the two sides of the sample.
The transverse voltage is the hall voltage VH and its magnitude is equal to IB/qnd, where I is the current, B is the magnetic field, d is the sample thickness and q is the elementary charge. A silver ribbon lies as shown in the adjacent figure. (z1=11.8mm and y1=0.23mm) carrying a current of 120A in the x-direction in a uniform magnetic field B=0.95T. If electron density is 5.85×1028/m3, then
Magnitude of the drift velocity of elelctrons is
View Solution
Knowledge Check
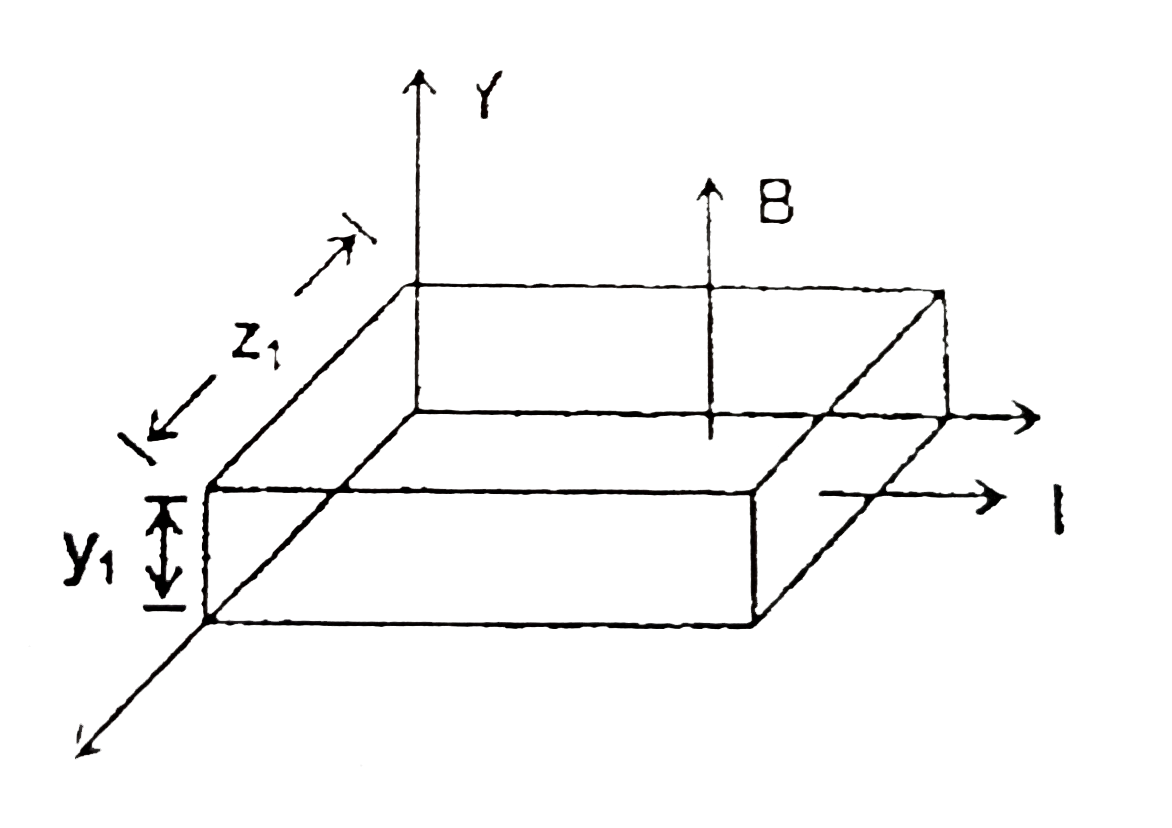
The basic principle underlying the hall effect is the Lorentz force. Whenk an electron moves along a direction perpendicular to an applied magnetic field. It exeriences a force acting normal to both the directions and moves in response to this force and the force exerted by the internal electric field. For an - n-type bar shaped semiconductor, the carries are predominatly electrons of bulk density n. We assume that the constant current I flows along the x-axis from left to right in the presence of a magnetic field toward the negative z-axis resulting in an excess surface electrical charge on the sides of the sample. this charge results in the hall voltage a potential drop across the two sides of the sample
Thre transverse voltage is the hall voltage VH and its magnitude is equal to IB/qnD, where I is the current B is the magnetic field, d is the sample thickness and q is the elementary charge. A silver ribbon lies as shown in the adjacent figure (z1=11.8mm and = 0.23 mm) carrying a current of 120 A in the x -direction in unifrom magnetic field B = 0.95 T. If electron density is 5.85×1028/m3 then
What is the magnitude and direction of electric field ?A4.5×10−3 V/m in + z dirB45×10−3 V/m In - z dirC2.25×10−3 V/m + x dirD2.25×10−3 V/m In - zdirThe basic principle underlying the hall effect is the Lorentz force. Whenk an electron moves along a direction perpendicular to an applied magnetic field. It exeriences a force acting normal to both the directions and moves in response to this force and the force exerted by the internal electric field. For an - n-type bar shaped semiconductor, the carries are predominatly electrons of bulk density n. We assume that the constant current I flows along the x-axis from left to right in the presence of a magnetic field toward the negative z-axis resulting in an excess surface electrical charge on the sides of the sample. this charge results in the hall voltage a potential drop across the two sides of the sample
Thre transverse voltage is the hall voltage VH and its magnitude is equal to IB/qnD, where I is the current B is the magnetic field, d is the sample thickness and q is the elementary charge. A silver ribbon lies as shown in the adjacent figure (z1=11.8mm and = 0.23 mm) carrying a current of 120 A in the x -direction in unifrom magnetic field B = 0.95 T. If electron density is 5.85×1028/m3 then
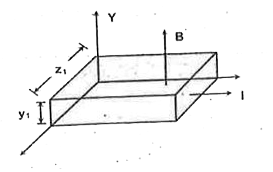
What is the value of hall emf?A53 mvB53μVC5.3 mVD5.3μVIf an electron is going in the direction of magnetic field →B with the velocity of →v then the force on electron is
AZeroBe(→v.→B)Ce(→v×→B)DNone of these
What is the force acting on charge (q) moving in a direction perpendicular to a magnetic field (B) with velocity v?
View SolutionWhat is the magnitude and direction of force on an electron moving along the direction of the magnetic field.
View SolutionAn electron in moving along positive x-axis in the presence of uniform magnetic field along positive y-axis. What is the direction of the force acting on it ?
View SolutionAn electrons is moving along +ve x-axis in the presence of uniform magnetic field along +ve y-axis. What is the direction of the force acting on it?
View SolutionAssertion : Magnetic force is always perpendicualr to the magnetic field.
Reason : Electric force is along the direction of electric field.
View Solution
