An inductor of inductance 2 mH is connected across a charged capacitor of 5 μ F . Let q denote the instaneous charge on the capacitor and i the current in the circuit . Maximum value of q is Q = 200 μ C.
(a) When q = 100 μ C what is the value of /di/dt / ?
(b) When q = 200 μ C what is the value of i ?
To solve the problem step by step, we will address both parts of the question.
Given Data:
- Inductance, L=2mH=2×10−3H
- Capacitance, C=5μF=5×10−6F
- Maximum charge, Q=200μC=200×10−6C
(a) When q=100μC, find didt.
1. Apply Kirchhoff's Voltage Law (KVL):
- The voltage across the inductor is given by −Ldidt.
- The voltage across the capacitor is given by −qC.
- According to KVL, we have:
−Ldidt−qC=0
- Rearranging gives:
Ldidt=−qC
2. Substitute the values:
- Substitute q=100μC=100×10−6C and the values of L and C:
Ldidt=−100×10−65×10−6
- This simplifies to:
Ldidt=−20
3. Calculate didt:
- Now, substituting L=2×10−3:
2×10−3didt=−20
- Thus,
didt=−202×10−3=−10,000A/s=−104A/s
(b) When q=200μC, find i.
1. Current at maximum charge:
- When the charge q=200μC, it indicates that the capacitor is fully charged and there is no change in charge at that instant.
- Therefore, the current i is given by:
i=dqdt
- Since q is at its maximum and does not change, we have:
dqdt=0
- Thus, the current i=0.
Final Answers:
(a) didt=−104A/s
(b) i=0A
- Inductance, L=2mH=2×10−3H
- Capacitance, C=5μF=5×10−6F
- Maximum charge, Q=200μC=200×10−6C
- The voltage across the inductor is given by −Ldidt.
- The voltage across the capacitor is given by −qC.
- According to KVL, we have:
−Ldidt−qC=0
- Rearranging gives:
Ldidt=−qC
- Substitute q=100μC=100×10−6C and the values of L and C:
Ldidt=−100×10−65×10−6
- This simplifies to:
Ldidt=−20
- Now, substituting L=2×10−3:
2×10−3didt=−20
- Thus,
didt=−202×10−3=−10,000A/s=−104A/s
- When the charge q=200μC, it indicates that the capacitor is fully charged and there is no change in charge at that instant.
- Therefore, the current i is given by:
i=dqdt
- Since q is at its maximum and does not change, we have:
dqdt=0
- Thus, the current i=0.
(a) didt=−104A/s
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - SOLVED PROBLEMS ( SUBJECTIVE)10videos
ELECTROMAGNETIC INDUCTION
- BOOK - FIITJEECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - SOLVED PROBLEMS ( OBJECTIVE)15videos
ELECTROMAGNETIC INDUCTION
- BOOK - FIITJEECHAPTER - ELASTICITY AND WAVES EXERCISE - Assignment Problems (Objective) Level-II15videos
ELASTICITY AND WAVES
- BOOK - FIITJEECHAPTER - ELECTROMAGNETIC INDUCTION AND AC CURRENTEXERCISE - Example15videos
ELECTROMAGNETIC INDUCTION AND AC CURRENT
Similar Questions
An inductor of inductance 2.0mH s connected across a charged capacitor of capacitance 5.0μF and the resulting LC circuit is set oscillating at its natural frequency. Let Q denote the instantaneous charge on the capacitor and I the current in the circuit. It is found that the maximum value of charge Q is 200μC.
a. When Q=100μC, what is the value of ∣∣∣dIdt∣∣∣?
b. When Q=200μC, what is the value of I?
c. Find the maximum value of I.
d. When I is equal to one-half its maximum value, what is the value of |Q|?View SolutionAn inductor of inductance 2.0mH is connected across a charged capacitor of capacitance 5.0μF and the resulting L−C circuit is set oscillating at its natural frequency. Let Q denote the instantaneous change on the capacitor and i the current in the circuit. It is found that the maximum value of Q is 200μC .
(a) When Q=100μC , what is the value of |di/dt| ?
(b) When Q=200μC , what is the value of i ?
(c)Find the maximum value of i
(d) When i is equal to one-half its maximum value, what is the value of |Q| ?View Solution
Knowledge Check
- Question 1 - Select One
An inductor of inductance 2.0 mH is connected across a charged capacitor of capacitance 0.5μF and the resulting LC circuit is set oscillating at its natural frequency. Let Q denote the instantaneous charge on the capacitor and I the current in the circuit. it is found that the maximum value of charge Q is 200μC. what is the maximum value of I (in ampere)?
A1AB1.5AC2AD3A - Question 2 - Select One
An inductor of inductance 2 mH is connected across a charged capacitor of capacitance 5μF and the L-C circuit is set oscillating at its natural frequency. What is the natural angular frequency of its oscillations?
A2×103rad/sB104rad/sC2×104rad/sD0.5×105rad/s - Question 3 - Select One
When a charged capacitor is made to discharge through an inductance, the charge Q on the capacitor and the current i in the inducrtor vary sinusoidally. The phase different between Q and i is
AπBπ2Cπ4Dzero
Determine the charge on the capacitor in the following circuit in μC ________.
 View Solution
View SolutionIn the circuit shown , charge on the 5μF capacitor is :
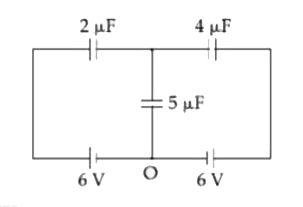 View Solution
View SolutionAn inductor of inductance 20 mH is connected across a charged capacitor of capacitance 5 μF & resulting L-C circuit is set oscillating at its natural frequency . The maximum charge q is 200 μ C on the capacitor . Find the potential difference across the inductor when the charge is 100 μC .
View SolutionAn LC circuit oscillating at natural frequency conssts of an inductor of inductance 30 m H and a capacitor of capacitance 60μF. The maximum value of instantaneous charge on capacitor in the circuit is 200 μC . If I is the current in the circuit then answer the following :
(i) What is the value of dIdt when charge is 150 μC?
(ii) Calculate the value of I when charge is 200 μC .
(iii) Find the maximum value of I.
(iv) For what value of q I is half of its maximum value ?View SolutionA non-resistive inductor is connected across a fully charged capacitor and the L-C circuit is set oscillating at its natural frequency. What is the value of the current when the charge on the capacitor has the maximum value of 100μC?
View Solution

