A capacitor can be used to produce a desired electric field. We consldered the parallel plate arrangement as a basic type of capacitor. Similarly, an inductor (symbol ) con be used to near the middle of a long solenoid ) as our basic type fo inductor.
if we establish a current i in the winding ( or turns ) of an inductro ( a solenoid ) the current produces a magnetic flux through the central region of the inductor. the inductance of the inductor is then
( inductance defined )
where N is the number of turns. the windings of the inductor are said to the linked by the shared flux, and the product is called the magnetic flux linkage . the inductance L is thus a measure of flux produced by the inductor per unit of current . Now, consider a special type of inductor whose radius of turn R as shown in the adjacent figure and total number of turns is N.
This special type of solenoid produces a magnetic field uniformly along the axis of the solenoid as shown in figure. r is the distance from the axis of solenoid.
![A capacitor can be used to produce a desired electric field. We consldered the parallel plate arrangement as a basic type of capacitor. Similarly, an inductor (symbol ) con be used to near the middle of a long solenoid ) as our basic type fo inductor. if we establish a current i in the winding ( or turns ) of an inductro ( a solenoid ) the current produces a magnetic flux phi(B) through the central region of the inductor. the inductance of the inductor is then [ L = (N phi(E))/(i) ] ( inductance defined ) where N is the number of turns. the windings of the inductor are said to the linked by the shared flux, and the product N phi(E ) is called the magnetic flux linkage . the inductance L is thus a measure of flux produced by the inductor per unit of current . Now, consider a special type of inductor whose radius of turn R as shown in the adjacent figure and total number of turns is N. This special type of solenoid produces a magnetic field |vec(B)| = mu l r^(2) uniformly along the axis of the solenoid as shown in figure. r is the distance from the axis of solenoid. The value of total flux linkages when current l flows through this special type of inductor is given by](https://d10lpgp6xz60nq.cloudfront.net/physics_images/FIITJEE_PHY_MB_05_C02_E03_001_Q01.png)
The value of total flux linkages when current l flows through this special type of inductor is given by
The correct Answer is:A
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - COMPREHENSIONS - II3videos
ELECTROMAGNETIC INDUCTION
- BOOK - FIITJEECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - COMPREHENSIONS - III2videos
ELECTROMAGNETIC INDUCTION
- BOOK - FIITJEECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT PROBLEMS (Level - II)15videos
ELECTROMAGNETIC INDUCTION
- BOOK - FIITJEECHAPTER - ELASTICITY AND WAVES EXERCISE - Assignment Problems (Objective) Level-II15videos
ELASTICITY AND WAVES
- BOOK - FIITJEECHAPTER - ELECTROMAGNETIC INDUCTION AND AC CURRENTEXERCISE - Example15videos
ELECTROMAGNETIC INDUCTION AND AC CURRENT
Similar Questions
The capacitor of capacitance C can be charged (with the help of a resistance R ) by a voltage source V, by closing switch S1 while keeping switch S2 open. The capacitor can be connected in series with an inductor 'L' by closing switch S2 and opening S1.

Initially, the capacitor was uncharged. Now , switch S1 is closed and S2 is kept open. if time constant of this circuit is τ, then02:35View SolutionA uniform wire of mass m and length I can freely slide on a pair of parallel, frictionless, horizontal rails placed in a vertical constant magnetic field B (as shown in figure ). The rails are connected by a capacitor of capacitance C. The electric resistance of the circuit is zero. A constant horizontal force F acts on the middle point of wire begining t = 0 ,and the wire is at rest t = 0.

At t = 0 , electric current in the circuit is03:42View SolutionA long wire carrying a steady current I lies in the plane of circular conducting loop placed at a certain distance from the wire. There will be an induced current in the loop if it is
04:16View SolutionWhen does an elastic metal rod change its length?
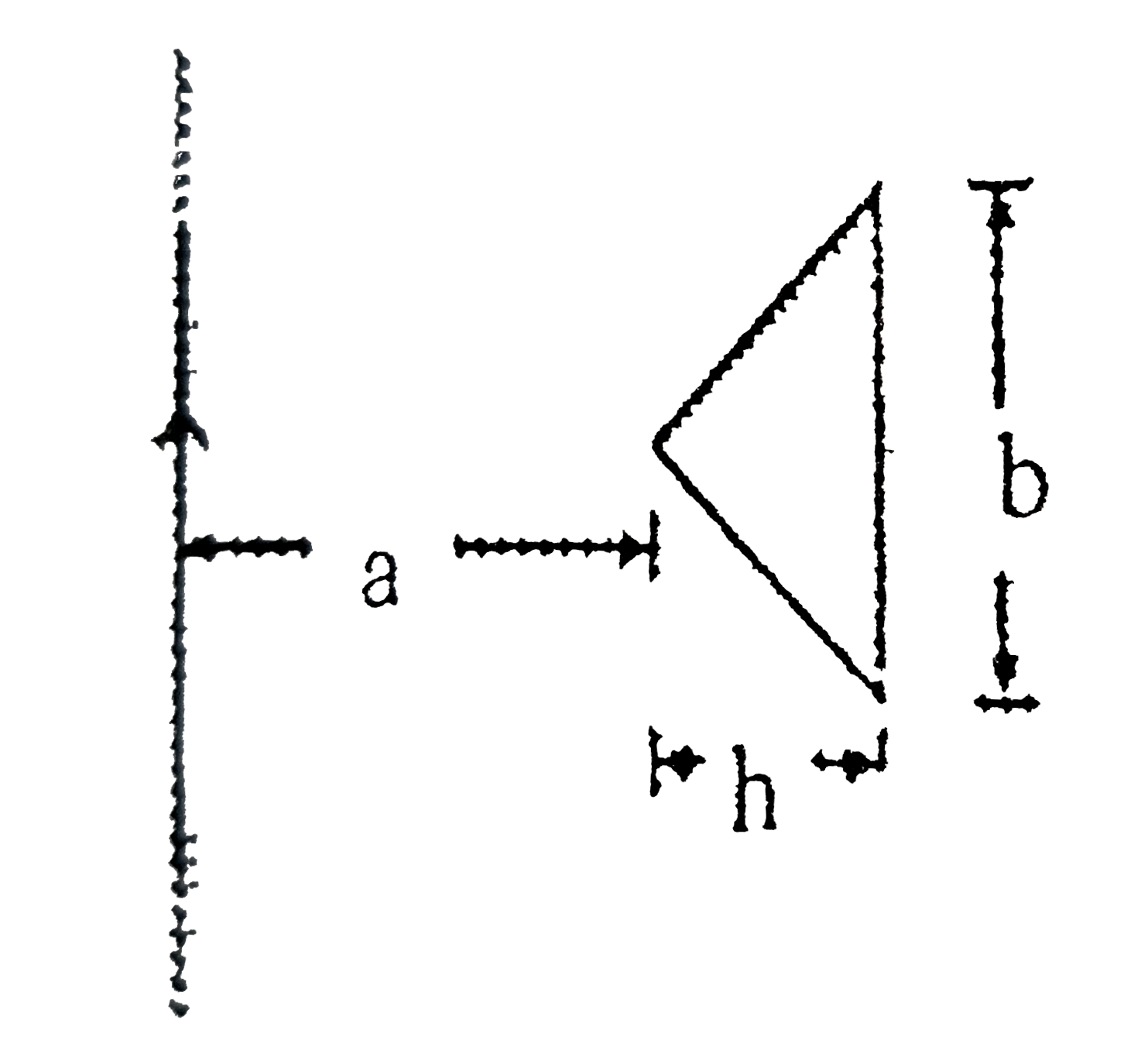
04:34View SolutionA very long staright conductor and an isoceles triangular conductor lie in a plane and separated from each other as shown in the figure.
Given a=10cm, b=20cm and h=10cm
(a) Find their coefficeint of mutual induction.
(b) If current in the staright wire is increasing at a rate of 2A/s , find the direction and magnitude of current in the triangular wire. [Diameter of the wire crosss-section d=1mm, resistivity of the wire, ρ=1.8×10−8Ω−m]
 03:34View Solution
03:34View SolutionA long solenoid is formed by winding 20 turns cm−1. What current is necessary to produce a magnetic field of 20mT inside the solenoid?
02:37View SolutionA capacitor and an inductor are connected in parallel across an ac source If the current through the inductor is 0.4 A and that through the capacitor is 0.3 A then the current drawn from the source is .
View SolutionA 90 cm long solenoid has six layers of windings of 450 turns each. If the diameter of solenoid is 2.2 cm and current carried is 6 A, then the magnitude of magnetic field inside the solenoid, near its centre is
View SolutionA closely wound solenoid 80cm long has 5 layers of windings of 400 turns each .The diameter of the solenoid is 1.8cm .If the current carried is 8A ,the magnetic field near the centre of the solenoid is ...
View SolutionWhy inductors or capacitors are used in AC circuits for controlling currents ?
View SolutionThe magnetic field intensity inside a long solenoid is 1T. If the current per turn of the solenoid winding is 1A, find the number of turns in per meter.
02:56View SolutionA capacitor can be used to produce a desired electric field. We consldered the parallel plate arrangement as a basic type of capacitor. Similarly, an inductor (symbol ) con be used to near the middle of a long solenoid ) as our basic type fo inductor.
if we establish a current i in the winding ( or turns ) of an inductro ( a solenoid ) the current produces a magnetic flux ϕB through the central region of the inductor. the inductance of the inductor is then
[L=NϕEi] ( inductance defined )
where N is the number of turns. the windings of the inductor are said to the linked by the shared flux, and the product NϕE is called the magnetic flux linkage . the inductance L is thus a measure of flux produced by the inductor per unit of current . Now, consider a special type of inductor whose radius of turn R as shown in the adjacent figure and total number of turns is N.
This special type of solenoid produces a magnetic field ∣∣→B∣∣=μlr2 uniformly along the axis of the solenoid as shown in figure. r is the distance from the axis of solenoid.
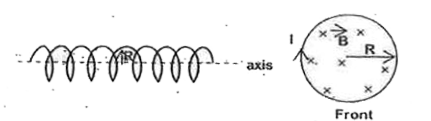
Value of self inductance of this inductor is given by02:09View SolutionA capacitor can be used to produce a desired electric field. We consldered the parallel plate arrangement as a basic type of capacitor. Similarly, an inductor (symbol ) con be used to near the middle of a long solenoid ) as our basic type fo inductor. if we establish a current i in the winding ( or turns ) of an inductro ( a solenoid ) the current produces a magnetic flux phi_(B) through the central region of the inductor. the inductance of the inductor is then [ L = (N phi_(E))/(i) ] ( inductance defined ) where N is the number of turns. the windings of the inductor are said to the linked by the shared flux, and the product N phi_(E ) is called the magnetic flux linkage . the inductance L is thus a measure of flux produced by the inductor per unit of current . Now, consider a special type of inductor whose radius of turn R as shown in the adjacent figure and total number of turns is N. This special type of solenoid produces a magnetic field |vec(B)| = mu l r^(2) uniformly along the axis of the solenoid as shown in figure. r is the distance from the axis of solenoid. If an external magneitc field vec(B) perperdicular to the axis of the solenoid is applied, then total flux linkage will
01:31View SolutionA capacitor can be used to produce a desired electric field. We consldered the parallel plate arrangement as a basic type of capacitor. Similarly, an inductor (symbol ) con be used to near the middle of a long solenoid ) as our basic type fo inductor.
if we establish a current i in the winding ( or turns ) of an inductro ( a solenoid ) the current produces a magnetic flux ϕB through the central region of the inductor. the inductance of the inductor is then
[L=NϕEi] ( inductance defined )
where N is the number of turns. the windings of the inductor are said to the linked by the shared flux, and the product NϕE is called the magnetic flux linkage . the inductance L is thus a measure of flux produced by the inductor per unit of current . Now, consider a special type of inductor whose radius of turn R as shown in the adjacent figure and total number of turns is N.
This special type of solenoid produces a magnetic field ∣∣→B∣∣=μlr2 uniformly along the axis of the solenoid as shown in figure. r is the distance from the axis of solenoid.

If it is given that total flux linkage through the inductor is KIL2 (where L is the inductance). then its inductance is given by03:37View SolutionA capacitor can be used to produce a desired electric field. We consldered the parallel plate arrangement as a basic type of capacitor. Similarly, an inductor (symbol ) con be used to near the middle of a long solenoid ) as our basic type fo inductor.
if we establish a current i in the winding ( or turns ) of an inductro ( a solenoid ) the current produces a magnetic flux ϕB through the central region of the inductor. the inductance of the inductor is then
[L=NϕEi] ( inductance defined )
where N is the number of turns. the windings of the inductor are said to the linked by the shared flux, and the product NϕE is called the magnetic flux linkage . the inductance L is thus a measure of flux produced by the inductor per unit of current . Now, consider a special type of inductor whose radius of turn R as shown in the adjacent figure and total number of turns is N.
This special type of solenoid produces a magnetic field ∣∣→B∣∣=μlr2 uniformly along the axis of the solenoid as shown in figure. r is the distance from the axis of solenoid.
 Adjust the value of K such that inductance become twice of the previous value. 02:42View Solution
Adjust the value of K such that inductance become twice of the previous value. 02:42View Solution

