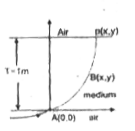
A ray of light travelling in air is incident at grazing angle (incident angle = 90∘) on a large rectangular slab of a transparent medium of thickness t = 1 m. The point of incidence js the origin A (0, 0). The medium has a refractive index of n (y) given
n(y)=(9ky32+1)12
Where K = (meter)−32, The refractive index of air is 1.
Obtain the equation for the trajectory y(x) of the ray of the medium.
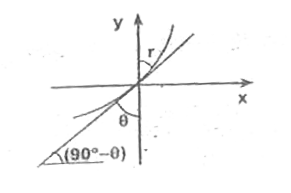
If θ be the incident angle, the slope of the curve (trajectory) at any point,
m=tan(90∘−θ)=cotθ
Since, sinθ1sinθ2=n2n1⇒n1sinθ1=n2sinθ2
If the ray is incident from the air on the medium at an angle
θ1=90∘ then sinθ1=1 and n1=1
⇒n2sinθ2=1⇒sinθ2=1n
Putting θ2=θ we obtain,
⇒sinθ=1n⇒cotθ=√n2−1
Since m=dydx=cotθ⇒dydx=√n2−1
Since n=√ky3/2+1
we obtain dydx=√ky3/2
4y1/4=k1/2x
Topper's Solved these Questions
- OPTICSBOOK - FIITJEECHAPTER - OPTICSEXERCISE - Solved problem (objective)
15 Videos
- OPTICSBOOK - FIITJEECHAPTER - OPTICSEXERCISE - Comprehension-1(prob)
3 Videos
- OPTICSBOOK - FIITJEECHAPTER - OPTICSEXERCISE - Illustration
10 Videos
- MODERN PHYSICSBOOK - FIITJEECHAPTER - MODERN PHYSICSEXERCISE - Numerical based questions
5 Videos
- PHYSICS PART-IIIBOOK - FIITJEECHAPTER - PHYSICS PART-IIIEXERCISE - NUMERICAL BASED QUESTIONS DECIMAL TYPE
11 Videos
Similar Questions
A ray of light travelling in air is incident at grazing angle (incident angle=90∘) on a long rectangular slab of a transparent medium of thickness t=1.0 (see figure). The point of incidence is the origin A(O,O) .The medium has a variable index of refraction n(y) given by :n(y)=[ky3/2+1]1/2 ,where k=1.0m−3/2.the refractive index of air is 1.0<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/NG_PHY_RO_C01_E01_029_Q01.pngwh=80%mx-autosty≤=background:white;><br>(i)Obta∈arelationbetweentheslopeofthetrajec→ryoftherayatap∮B(x,y)∈themediumandthe∈cnt∠attˆp∮<br>(ii)obta∈anequationforthetrajec→ryy(x)oftheray∈themedium.<br>(ii)Determinethec∞rd∈ates(x_(1),y_(1))ofthep∮P.where the ray the ray intersects upper surface of the slab -air boundary.
Indicate the path of the ray subsequently.
View SolutionA ray of light travelling in air is incident at grazing angle (incident angle=90∘) on a long rectangular slab of a trasnparent medium of thickness t=1.0(see figure). The point of incidence is the originA(O,O) .The medium has a variable index of refraction n(y) given by :n(y)=[ky3/2+1]1/2,wherek=1.0m−3/2.the refrative index of air is 1.0<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/NG_PHY_RO_C01_E01_029_Q01.pngwh=80%mx-autosty≤=background:white;><br>(i)Obta∈arelationbetweentheslopeofthetrajec→ryoftherayatap∮B(x,y)∈themediumandthe∈cnt∠attˆp∮<br>(ii)obta∈anequationforthetrajec→ryy(x)oftheray∈themedium.<br>(ii)Determinethec∞rd∈ates(x_(1),y_(1))ofthep∮P.where the ray the ray intersects upper surface of the slab -air boundary.
Indicate the path of the ray subsequently.
View Solution
Knowledge Check
A ray of light travelling in air is incident at 45∘ on a medium of refractive index √2. The angle of refractive in the medium is
AA. 45∘BB.60∘CC.30∘DD.70∘AN unpolarised beam of light is incident at the polarising angle on the surface of a transparent medium of refractive index 1.6. The angle of refraction in the medium is
A58∘B29∘C32∘D42∘
A light ray enters from medium A to medium B as shown in the figure. The refractive index of medium B relative to A will be
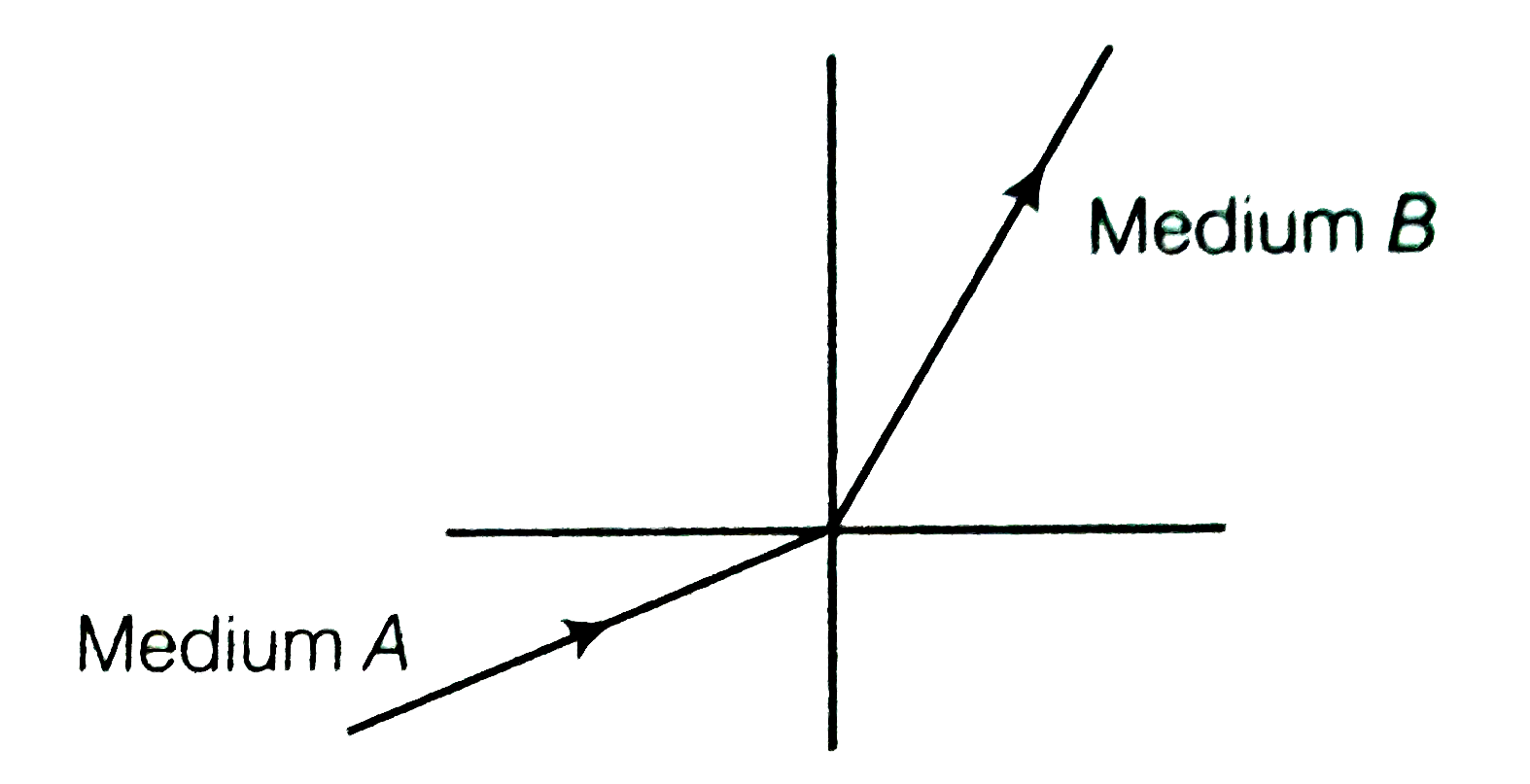
View SolutionA ray of light travelling in air is incident on the plane surface of a transparent medium. The angle of incidence is 45∘ and the angle of refraction is 30∘ . Find the refractive index of the medium .
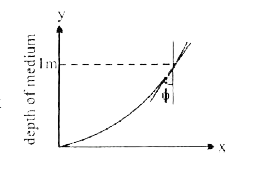
View SolutionA ray of light travelling in air is incident at grazing angle (incidence angle =90∘) on a medium whose refractive index depends on the depth of the medium. The trajectory of the light in the medium is a parabola, y=2x2. Find, at a depth of 1 m in the medium
(i) the refractive index of the medium and
(ii) angle of incidence ϕ.
View SolutionThe lateral shift for a ray of light incident at 60∘ on one face of a rectangular slab of thickness 1 m is 0.577 m. What is the refractive index of the slab.
View SolutionA ray of light is incident at an angle of 60∘ on one face of a rectangular glass slab of thickness 0.1m, and refractive index 1.5.Calculate the lateral shift produced.
View SolutionWhen a light ray moves from air to a transparent medium the angle of incidence and the angle of refraction are 45∘and30∘ respectively. Find the refractive index of this medium.
View Solution
