Question

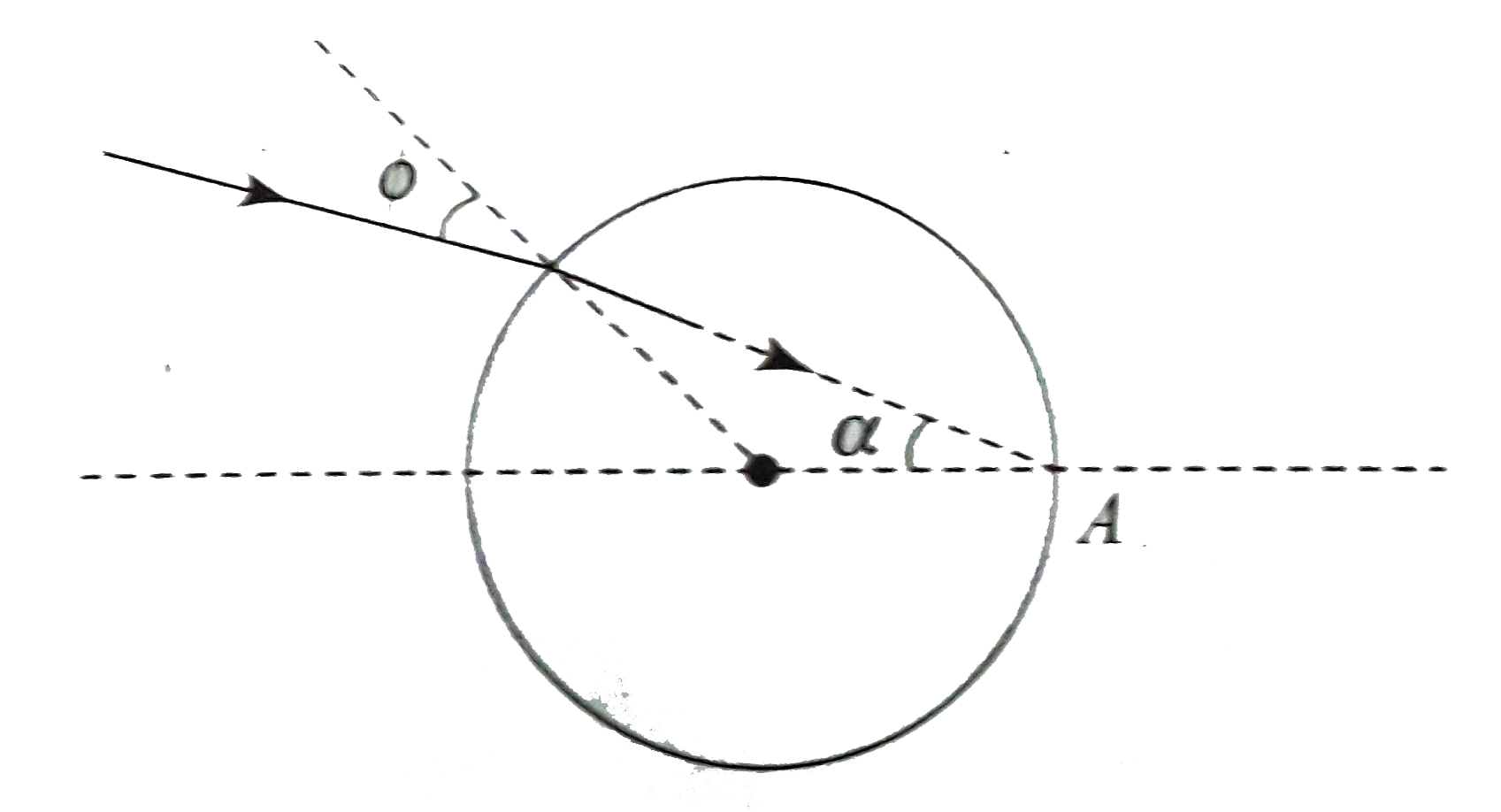
Two parallel beams of light P and Q (separation d) containing radiation of wavelengths $4000A$ and $5000A$ (which are mutually coherent in each wavelength separately) are incident normally on a prism as shown in fig. The refractive index of the prism as a function of wavelength is given by the relation. $\mu \left(\lambda \right)=1.20+\frac{b}{{\lambda }^2}$ Where $\lambda$ is in $A$ and b is positive constant. The value of b is such that the condition wave length and is not satisfied for the other.
(a) Find the value of b.
(b) find the deviation of the beams transmitted through the face AC. (c) A convergent lens is used to bring these transmitted beams into focus. If the intensities of transmission form the face AC, are 41 and I respectively, find the resultant intensity at the focus.

Explanation

Similarly `delta_(2) = r_(2)- i_(2)` where `i_(2)= theta` & `r_(2)` can be given as
`(sini_(2))/(sin r_(2)) = 1/n_(2)`
Putting `n_(2) = 1.2 + b/(5000)^(2) = 1.2 + (0.8 xx 10^(6))/(5000)^(2)`
=1.232 and `sintheta=0.8`
We obtain `r_(2)=80^@ 16^(.)`
`implies delta_(2) = 80^@ 16^(.) - sin^(-1) 0.8 cong 27^@`