A rectangular block of glass (R.l. = 3/2) is kept in water (R.l. = 4/3). The critical angle for total internal reflection between glass and water is
sin−1(23)
sin−1(124)
tan−1(23)
tan−1(32)
The correct Answer is:A
To find the critical angle for total internal reflection between the glass and water, we can follow these steps:
Step 1: Identify the refractive indices
- The refractive index of glass (n_glass) is given as 32.
- The refractive index of water (n_water) is given as 43.
Step 2: Understand the condition for total internal reflection
Total internal reflection occurs when light travels from a denser medium (glass) to a rarer medium (water). The critical angle (θ_c) is the angle of incidence in the denser medium at which the angle of refraction in the rarer medium is 90 degrees.
Step 3: Apply Snell's Law
According to Snell's Law:
n1sin(θ1)=n2sin(θ2)
Where:
- n1=nglass=32
- n2=nwater=43
- θ1=θc (the critical angle)
- θ2=90∘
Since sin(90∘)=1, we can rewrite Snell's Law as:
32sin(θc)=43⋅1
Step 4: Solve for the critical angle
Rearranging the equation gives:
sin(θc)=43⋅23=89
Step 5: Calculate the critical angle
To find θc, we take the inverse sine:
θc=sin−1(89)
Final Answer
Thus, the critical angle for total internal reflection between the glass and water is:
θc=sin−1(89)
---
- The refractive index of glass (n_glass) is given as 32.
- The refractive index of water (n_water) is given as 43.
Total internal reflection occurs when light travels from a denser medium (glass) to a rarer medium (water). The critical angle (θ_c) is the angle of incidence in the denser medium at which the angle of refraction in the rarer medium is 90 degrees.
According to Snell's Law:
n1sin(θ1)=n2sin(θ2)
Where:
- n1=nglass=32
- n2=nwater=43
- θ1=θc (the critical angle)
- θ2=90∘
32sin(θc)=43⋅1
Rearranging the equation gives:
sin(θc)=43⋅23=89
To find θc, we take the inverse sine:
θc=sin−1(89)
Thus, the critical angle for total internal reflection between the glass and water is:
θc=sin−1(89)
Topper's Solved these Questions
- OPTICSBOOK - FIITJEECHAPTER - OPTICSEXERCISE - ASSERTION REASONING TYPE
3 Videos
- OPTICSBOOK - FIITJEECHAPTER - OPTICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE)(level 2)
20 Videos
- OPTICSBOOK - FIITJEECHAPTER - OPTICSEXERCISE - assignment problem(subjective)(Level - II & III)
15 Videos
- MODERN PHYSICSBOOK - FIITJEECHAPTER - MODERN PHYSICSEXERCISE - Numerical based questions
5 Videos
- PHYSICS PART-IIIBOOK - FIITJEECHAPTER - PHYSICS PART-IIIEXERCISE - NUMERICAL BASED QUESTIONS DECIMAL TYPE
11 Videos
Similar Questions
Knowledge Check
The critical angle for refraction from glass to air is 30° and that from water to air is 37° . Find the critical angle for refraction from glass to water
Asin−1(56)B51∘3'C61∘2'D63∘3'Relation between critical angles of water and glass is
ACw>CgBCw<CgCCw=CgDCw=Cg=0If sound travelling at 340ms−1 enters water where its speed becomes 1480ms−1 , then critical angle for total internal reflection is
A13.3∘B89.7∘C86.7∘D10.3∘
A ray of light strikes a glass plate at an angle of incidence 57∘. If the reflected and refracted rays are perpendicular to eachother, calculate critical angle for total internal reflection at glass air interface.
View SolutionCritical Angle||Total Internal Reflection||Graph Between Deviation and Angle OF Incidence
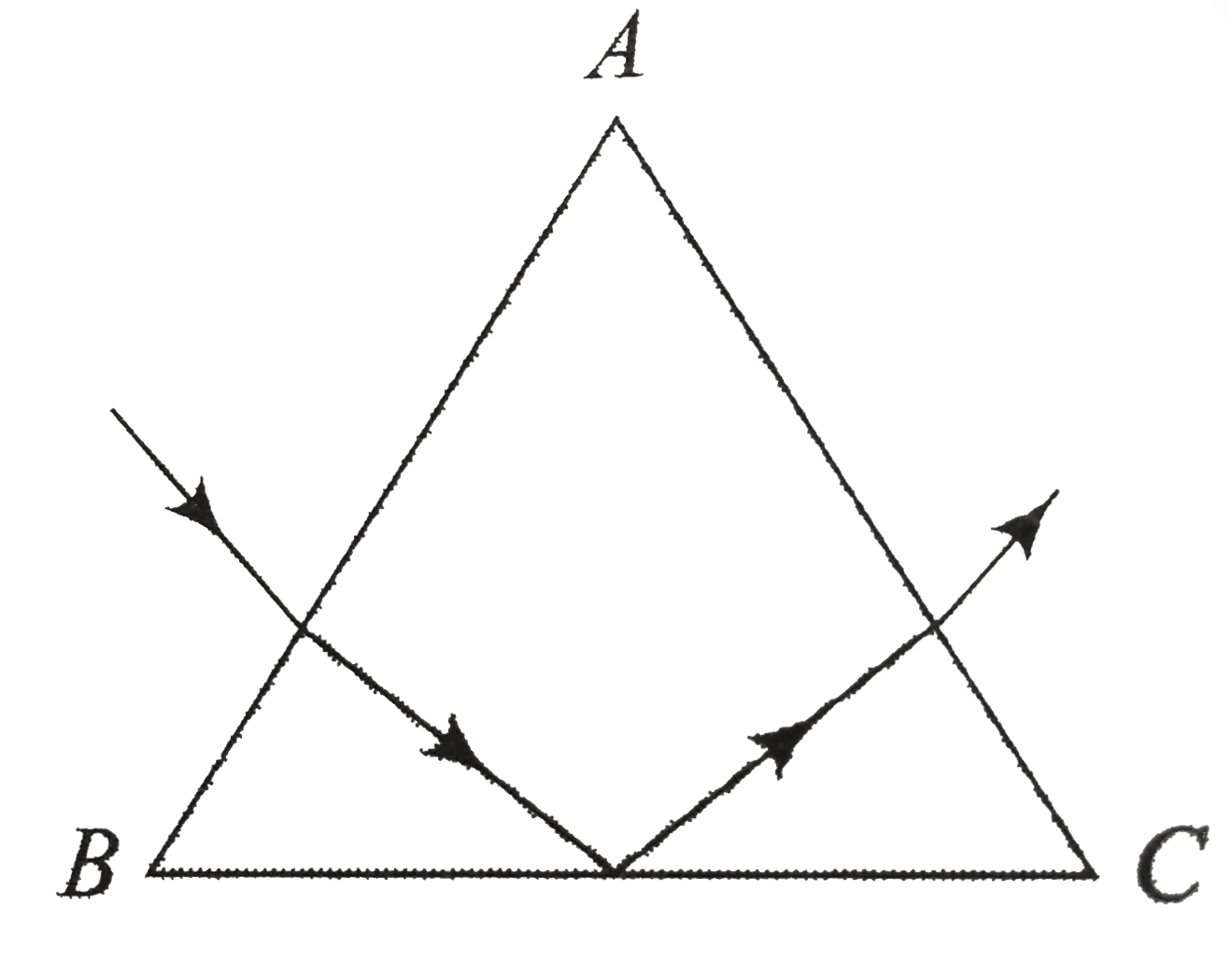
View SolutionThe path of a ray of light passing through an equilateral glass prism ABC is shown in figure. The ray of light is incident on face BC at the critical angle for just total internal reflection. The total internal reflection. The total angle of deviation after the refraction at face AC is 108∘. Calculate the refractive index of the glass.
View SolutionA light ray falls on a rectangular glass slab as shown. The index of refraction of the glass, if total internal reflection is to occur at the vertical face, is

View SolutionCritical angle of light passing from glass to water is minimum for
View Solution
