An optical fibre (mu = 1.72) is surrounded by a glass coating (mu= 1.50). Find the critical angle for total internal reflection at the fibre-glass interface.
The correct Answer is:A
To find the critical angle for total internal reflection at the fibre-glass interface, we can follow these steps:
1. Understand the Concept of Critical Angle:
The critical angle (C) is the angle of incidence above which total internal reflection occurs when light travels from a denser medium to a rarer medium.
2. Identify the Refractive Indices:
- The refractive index of the optical fiber (denser medium) is μ1=1.72.
- The refractive index of the glass coating (rarer medium) is μ2=1.50.
3. Use Snell's Law:
According to Snell's Law, at the critical angle, the relationship can be expressed as:
μ1sin(C)=μ2sin(90∘)
Since sin(90∘)=1, this simplifies to:
μ1sin(C)=μ2
4. Substitute the Values:
Substitute the values of the refractive indices into the equation:
1.72sin(C)=1.50
5. Solve for sin(C):
Rearranging the equation gives:
sin(C)=1.501.72
6. Calculate sin(C):
Performing the division:
sin(C)=1.501.72≈0.8721
7. Find the Critical Angle C:
To find the critical angle, take the inverse sine:
C=sin−1(0.8721)
8. Calculate the Angle:
Using a calculator, we find:
C≈61.0∘
Final Answer:
The critical angle for total internal reflection at the fibre-glass interface is approximately 61.0∘.
---
The critical angle (C) is the angle of incidence above which total internal reflection occurs when light travels from a denser medium to a rarer medium.
- The refractive index of the optical fiber (denser medium) is μ1=1.72.
- The refractive index of the glass coating (rarer medium) is μ2=1.50.
According to Snell's Law, at the critical angle, the relationship can be expressed as:
μ1sin(C)=μ2sin(90∘)
Since sin(90∘)=1, this simplifies to:
μ1sin(C)=μ2
Substitute the values of the refractive indices into the equation:
1.72sin(C)=1.50
Rearranging the equation gives:
sin(C)=1.501.72
Performing the division:
sin(C)=1.501.72≈0.8721
To find the critical angle, take the inverse sine:
C=sin−1(0.8721)
Using a calculator, we find:
C≈61.0∘
The critical angle for total internal reflection at the fibre-glass interface is approximately 61.0∘.
Topper's Solved these Questions
Similar Questions
A ray of light strikes a glass plate at an angle of incidence 57∘. If the reflected and refracted rays are perpendicular to eachother, calculate critical angle for total internal reflection at glass air interface.
View SolutionExplain briefly how the phenomenon of total internal reflection is used in fibre optics.
View Solution
Knowledge Check
A rectangular block of glass (R.l. = 3/2) is kept in water (R.l. = 4/3). The critical angle for total internal reflection between glass and water is
Asin−1(23)Bsin−1(124)Ctan−1(23)Dtan−1(32)Statement I: A ray is incident from outside on a glass sphere surrounded by air as shown in Figure. This ray may suffer total internal reflection at the second interface.

Statement II: For a ray going from a denser to rarer medium, the ray may suffer total internal reflection.AStatement is True, Statement II is True, Statement II is correct explanation for Statement IBStatement I is True, Statement II is True, Statement II is NOT a correct explanation for Statement I.CStatement I is True, Statement II is False.DStatement I is False, Statement II is True.In the diagram shown, a ray of light is incident on the interface between 1 and 2 at angle slightly greater than critical angle. The light surfers total internal reflection at this interface. After that the light ray falls at the interface of 1 and 3, and again it suffers total internal reflection. Which of the following relations should hold true?
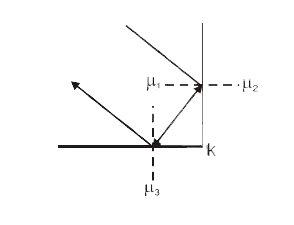 Aμ1>μ2<μ3Bμ21−μ22>μ23Cμ21−μ23>μ22Dμ21+μ22>μ23
Aμ1>μ2<μ3Bμ21−μ22>μ23Cμ21−μ23>μ22Dμ21+μ22>μ23
A ray of light is incident on a glass prism of refractive index μ and refractive angle A. If it just suffers total internal reflection at the other face, obtain an expression relating the angle of incidence , angle of prism and critical angle.
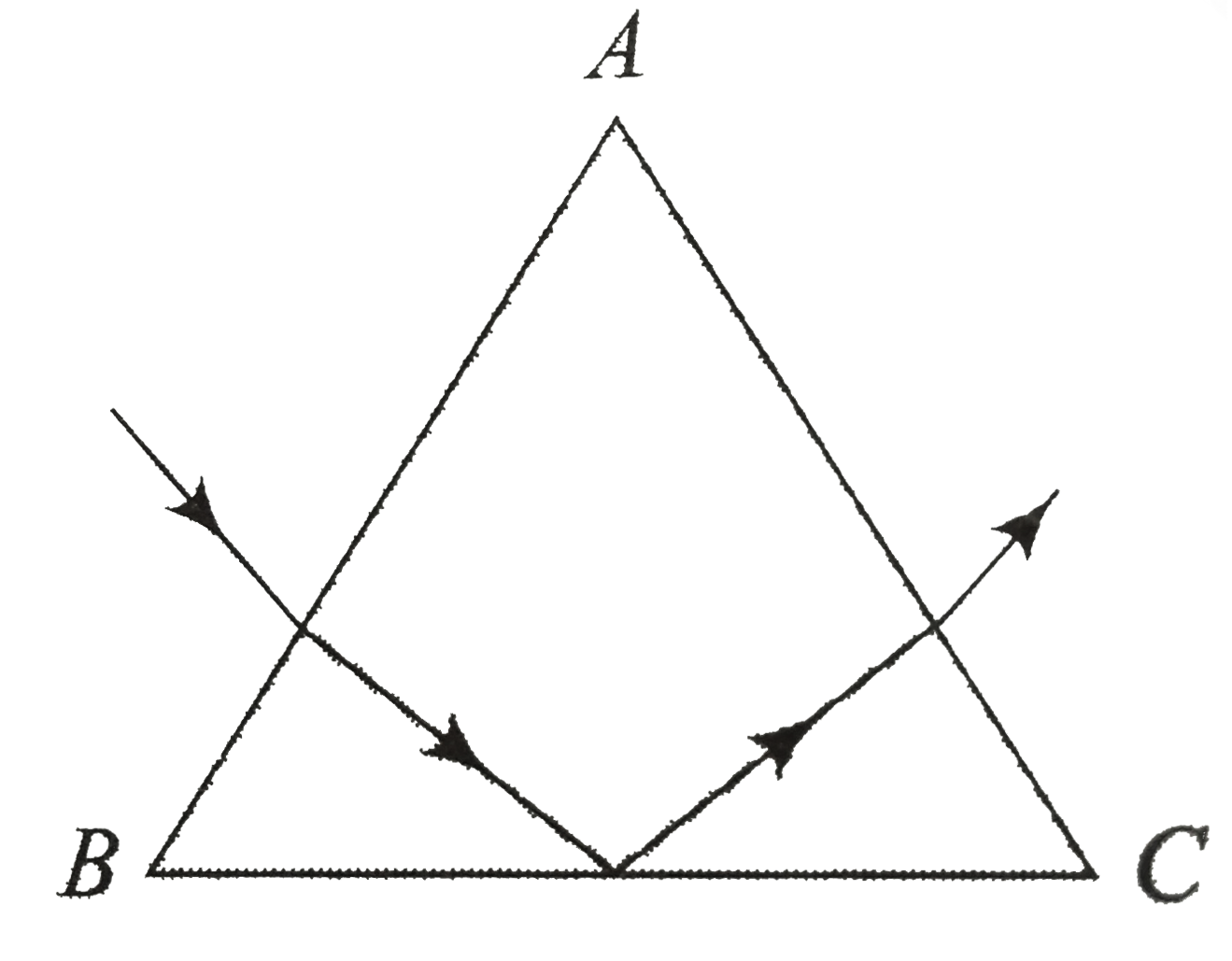
View SolutionThe path of a ray of light passing through an equilateral glass prism ABC is shown in figure. The ray of light is incident on face BC at the critical angle for just total internal reflection. The total internal reflection. The total angle of deviation after the refraction at face AC is 108∘. Calculate the refractive index of the glass.
View SolutionLight undergoes successive total internal reflection as it moves through an optical fibre.
View SolutionAn isosceles glass prism with base angles 40∘ is champed over a tray of water in a position such that the base is just dipped in water. A ray of light incident normally on the inclined face suffers total internal reflection at the base. If the refractive index of water is 1.33 then the condition imposed on the refractive index μ of the glass is -
View SolutionPick out the correct staments about optical fibres from the following:
S1: Optical fibres are used for the transmission of optical signals only
S2: Optical fibres are used for transmission of optical electrical signals
S3: The intensity of light signals sent through optical fibres suffer very small loss
S4: Optical fibres effectively employ the principle of multiple total internal reflections
S5: Optical fibres are glass fibres coated with a thin layer of a material with lower refractive index
View Solution
