For one mole of an ideal gas
The correct Answer is:A, B, C
Topper's Solved these Questions
- GASEOUS STATEBOOK - FIITJEECHAPTER - GASEOUS STATEEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-II COMPREHENSION-I
5 Videos
- GASEOUS STATEBOOK - FIITJEECHAPTER - GASEOUS STATEEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-II COMPREHENSION-II
4 Videos
- GASEOUS STATEBOOK - FIITJEECHAPTER - GASEOUS STATEEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-I
50 Videos
- ENVIRONMENTAL CHEMISTRYBOOK - FIITJEECHAPTER - ENVIRONMENTAL CHEMISTRYEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL -II (MULTIPLE CORRECT QUESTIONS)
20 Videos
- GENERAL ORGANIC CHEMISTRYBOOK - FIITJEECHAPTER - GENERAL ORGANIC CHEMISTRYEXERCISE - SINGLE INTEGER ANSWER TYPE QUESTIONS
14 Videos
Similar Questions
Knowledge Check
An ideal gas is initially at temperature T and volume V. Its volume is increased by ΔV due to an increase in temperature ΔT, pressure remaining constant. The quantity δ=ΔVVΔT varies with temperature as
A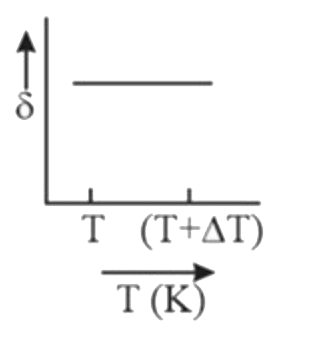 B
B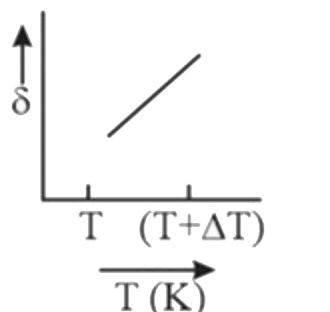 C
C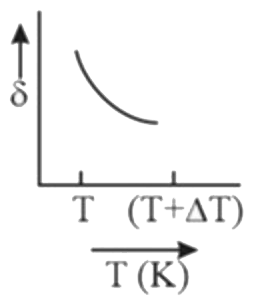 D
D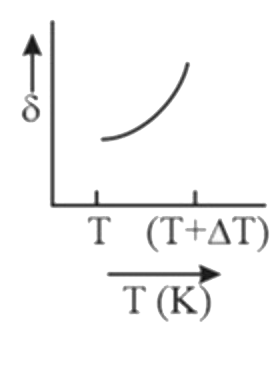
The expression [ΔE/ΔT]V represent
View SolutionA body is released from rest at t0=0,x0=0 and moves with constant acceleration. Its position is measured at the equally spaced times t1=Δt,t2=2Δt,t3=3Δt and so forth. Prove that displacements Δxj−xj−1 which occur in the successive time intervals Δt are in the ratio
Δx1:Δx2:Δx3......≈1:3:5...
View SolutionCompare the formula Cp−Cv=R for an ideal gas with the thermodynamics relation ΔU=ΔQ−PΔV.
View SolutionCompare the formula Cp−Cv=R for an ideal gas with the thermodynamics relation ΔU=ΔQ−PΔV.
View SolutionThe drift speed is defined as vd=(Δl/Δt)where (Δl)isthedistancedrifted∈alongtime(Delta t).Whydon'twedef∈ethedriftspeedasthelimitof(Delta l//Delta t)as (Delta t (rarr)0)?
View SolutionThe drift speed is defined as vd=(Δl/Δt)where (Δl)isthedistancedrifted∈alongtime(Delta t).Whydon'twedef∈ethedriftspeedasthelimitof(Delta l//Delta t)as (Delta t (rarr)0)?
View SolutionThe volume of one mode of an ideal gas with adiabatic exponent γ is varied according to the law V=a/T, where a is constant . Find the amount of heat obtained by the gas in this process, if the temperature is increased by ΔT.
View Solution
