Consider following figure and answer the questions at the end of it.
Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.
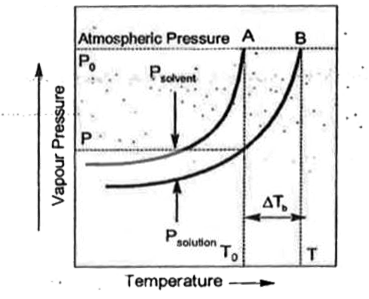
Variation of vapour pressure with temperature and showing elevation in boiling point.
Elevation in boiling point of an aqueous urea solution is . (. Hence, mole fraction of urea in this solution is
0.982
0.0567
0.943
0.018
The correct Answer is:D
Topper's Solved these Questions
- LIQUID SOLUTION BOOK - FIITJEECHAPTER - LIQUID SOLUTION EXERCISE - Comprehension - V
3 Videos
- LIQUID SOLUTION BOOK - FIITJEECHAPTER - LIQUID SOLUTION EXERCISE - Comprehension - VI
2 Videos
- LIQUID SOLUTION BOOK - FIITJEECHAPTER - LIQUID SOLUTION EXERCISE - Comprehension - III
4 Videos
- IONIC EQUILIBRIUM BOOK - FIITJEECHAPTER - IONIC EQUILIBRIUM EXERCISE - SINGLE INTEGER ANSWER QUESTIONS
4 Videos
- NUCLEIC ACID AND VITAMIN BOOK - FIITJEECHAPTER - NUCLEIC ACID AND VITAMIN EXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE)
15 Videos
Similar Questions
Figure explains elevation in boiling point when a non-volatile solute is added to a solvent. Variation of vapour pressure with temperaure and elevation in boiling point is marked.

Elevation in b.p of an aqueous urea solution is 0.52∘(Kb=0.52∘mol−1kg). Hence, mole fraction of urea in this solution is:
View SolutionConsider following figure and answer the questions at the end of it. Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.
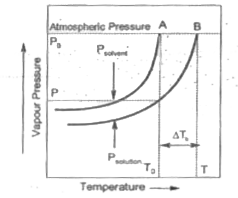
Variation of vapour pressure with temperature and showing elevation in boiling point.
A complex of iron and cyanide ions is 100% ionized at 1m (molal). If elevation in boiling point is 2.08∘(Kb=0.52∘mol−1kg) then the complex is:
View Solution
Knowledge Check
Figure explains elevation in boiling point when a non-volatile solute is added to a solvent. Variation of vapour pressure with temperaure and elevation in boiling point is marked.

Elevation in b.p of an aqueous urea solution is 0.52∘(Kb=0.52∘mol−1kg). Hence, mole fraction of urea in this solution is:A0.982B0.0567C0.943D0.018Elevation in b.p. of an aqueous urea solution is 0.52∘,(Kb=0.622∘mol−1kg) Hence, mole-fraction of urea in this solution is :
A0.982B0.567C0.943D0.018Consider following figure and answer the questions at the end of it. Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.

Variation of vapour pressure with temperature and showing elevation in boiling point.
A complex of iron and cyanide ions is 100% ionized at 1m (molal). If elevation in boiling point is 2.08∘(Kb=0.52∘mol−1kg) then the complex is:AK3[Fe(CN)6]BFe(CN)2CK4[Fe(CN)6]DFe(CN)4
Elevation in boiling point of an aqueous solution of urea is 0.52(kbfor water=0.52Kmolality−1). The mole fraction of urea in this solution is :
View SolutionConsider following figure and answer the questions at the end of it. Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.
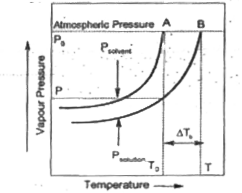
Variation of vapour pressure with temperature and showing elevation in boiling point.
Given that ΔTb is the elevation in boiling point of the solvent in a solution of molality m then Ltm→0(ΔTbm) is equal to
View SolutionConsider following figure and answer the questions at the end of it.
Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.
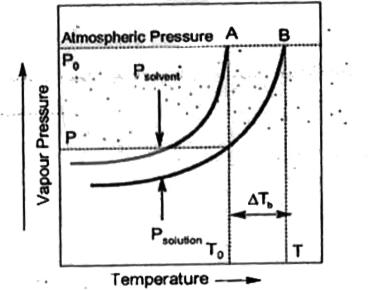
Variation of vapour pressure with temperature and showing elevation in boiling point.
A complex of iron and cyanide ions is 100% ionized at 1m (molal). If its elevation in boiling point is 2.08∘(Kb=0.52∘mol−1kg) then the complex is
View SolutionElevation in boiling point of an aqueous solution of urea is 0.52(kbfor water=0.52Kmolality−1). The mole fraction is urea in this solution is :
View SolutionConsider following figure and answer the questions at the end of it.
Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.
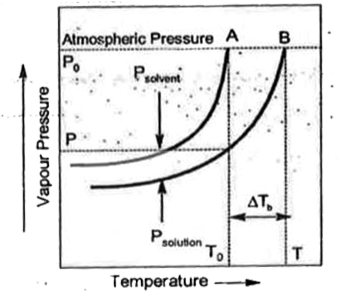
Variation of vapour pressure with temperature and showing elevation in boiling point.
Given that ΔTb is the elevation in boiling point of the solvent in a solution of molality 'm' then Ltm→0(DηlTbm) is equal to
View Solution
