A sequence b0,b1,b2,... is defined by letting b0=5 and bk=4+bk−1, for all natural number k. Show that bn=5+4n, for all natural number n using mathematical induction.
Step by step video & image solution for A sequence b_(0),b_(1),b_(2), . . . is defined by letting b_(0)=5 and b_(k)=4+b_(k-1), for all natural number k. Show that b_(n)=5+4n, for all natural number n using mathematical induction. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MATHEMATICAL INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL INDUCTIONEXERCISE - Revision Exercise
14 Videos
- MATHEMATICAL INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL INDUCTIONEXERCISE - CHECK YOUR UNDERSTANDING
10 Videos
- MATHEMATICAL INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL INDUCTIONEXERCISE - (OBJECTIVE TYPE QUESTIONS)(VERY SHORT ANSWER TYPE QUESTIONS)
5 Videos
- LINEAR INEQUATIONSBOOK - MODERN PUBLICATIONCHAPTER - LINEAR INEQUATIONSEXERCISE - CHAPTER TEST
12 Videos
- MATHEMATICAL REASONING BOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL REASONING EXERCISE - CHAPTER TEST 14
12 Videos
Similar Questions
Knowledge Check
Let a,b,c,d be any four real numbers , then an+bn=cn+dn holds for any natural number n, if
Aa+b=c+dBa−b=c−dCa+b=C+d,a2+b2=c2+d2Da−b−c−d,a2−b2=c2−d2If A={4n+2∣n is a natural number}andB={3n∣n is a natural number}, then what is (A∩B) equal to?
A{12n2+6n∣n is a natural number}B{24n−12∣n is a natural number}C{60n−30∣n is a natural number}D{12n−6∣n is a natural number}If A = {4n+ 2| n is a natural number} and B = {3n|n is a natural number}, then what is (A∩B) equal to?
A{12n2+6n∣∣n is a natural numberB{24n−12∣ n is a natural numberC{60n+30∣ n is a natural numberD{12n−6∣ n is a natural number
A sequence x1,x2,x3,.... is defined by letting x1=2 and xk=xk−1k for all natural numbers k,k≥2 Show that xn=2n! for all n∈N.
View SolutionFind the smallest natural number k such that k(33+43+53)=ab for some natural numbers a and b
View SolutionFind the smallest natural number k such that k(33+43+53)=ab for some natural numbers a and b
View SolutionComplete the following statements.
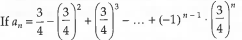 and bn=1−an then the smallest natural number n0, such that bn>anVntn>n0 is
and bn=1−an then the smallest natural number n0, such that bn>anVntn>n0 is
View SolutionShow by using the principle of mathematical induction that for all natural number n>2,2n>2n+1
View Solution
