A random variable X is defined by :
X=⎧⎪⎨⎪⎩3 with probability = 1/34 with probability = 1/412 with probability =5/12
Then E(X) is : Solution in Kannada
6
7
5
8
The correct Answer is:B
Step by step video, text & image solution for A random variable X is defined by : X={:{(3 " with probability = 1/3"),(4 " with probability = 1/4"),(12 " with probability =5/12"):} Then E(X) is : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROBABILITYBOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - MULTIPLE CHOICE QUESTIONS (LEVEL - II )
30 Videos
- PROBABILITYBOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - LATEST QUESTIONS FROM AIEEE/JEE EXAMINATIONS
13 Videos
- PERMUTATIONS AND COMBINATIONS BOOK - MODERN PUBLICATIONCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Recent Competitive Questions
6 Videos
- QUADRATIC EQUATIONS BOOK - MODERN PUBLICATIONCHAPTER - QUADRATIC EQUATIONS EXERCISE - LATEST QUESTIONS FROM AIEEE/JEE EXAMINATIONS
13 Videos
Similar Questions
LET A and B be the events such that P(A) = 0.3 and P(A∪B)=0.8 . If A and B are independent events , then P(B) is :
View SolutionAn urn contains nine balls of which three are red , four are blue and two are green . Three balls are drawn at random without replacement from the urn . The probability that the three balls have different colours is :
View SolutionHow many 5 digit telephone numbers can be constructed using the digits 0 to 9, if each number starts with 67 and no digit appears more than once ?
View SolutionLet p and q be real numbers such that p ≠ 0 , p3≠ q and p3≠−q. if αandβ are non-zero complex numbers satisfying α+β=−p and α3+β3=q,
then a quadratic equation having αβandβα as its roots is :
View SolutionWhich of the following distributions of probability of random variable X are the probability distributions? X: 0 1 2 3 4 P(X):0.1 0.5 0.2 0.1 0.1
View SolutionA random variable X is defined by
X=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩3 with probability=134 with probability=1412 with probability=512
Then, E(X) is
View SolutionThe probability distribution of a random variable (X) is P(X)={x12:X=1, 2, 3, 4, 5, 60:otherwise
Then, the conditional probability
P⎛⎝32<X<72X>2⎞⎠ is
View SolutionThe probability function of a random variable is defined as
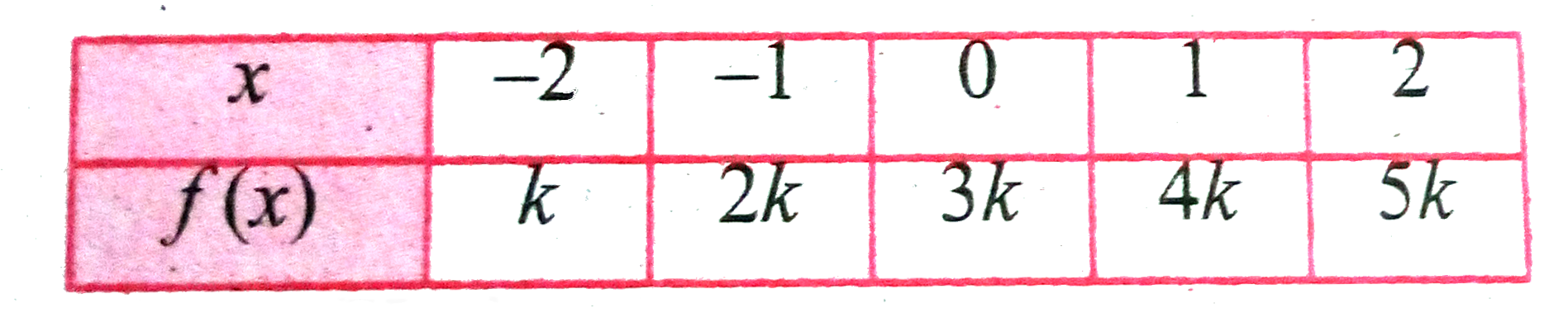
Then E(X) is equal to
View SolutionX is a random variable taking the values 3,4 and 12 with probabilites 13,14 and 512 then E(x) is
View Solutionf(x)=112,a<x<b எனும் சார்பு ஒரு தொடர்ச்சியான சமவாய்ப்பு மாறியின் நிகழ்தகவு அடர்த்தி சார்பினைக் குறிக்கிறது எனில், பின்வருவனவற்றுள் எது 1 மற்றும் –இன் மதிப்புகளாக இராது?
View SolutionA random variable X has the probability distribution:

For the events E = (X is prime number) and F = {X < 4}, the probability P(E∪F) is
View SolutionCheck the following distributions of probability of random variable X is the probability distributions?
X: 0 1 2
P(X):0.6 0.4 0.2
View SolutionProve that the following distributions of probability of random variable X are the probability distributions? X: 0 1 2 3 4 P(X):0.1 0.5 0.2 0.1 0.1
View SolutionA random variable X takes four values with probabilities 1+3x4,(1−x),1+2x4 and 1−4x4. Find the set of values of x for the variable X to have probability distribution.
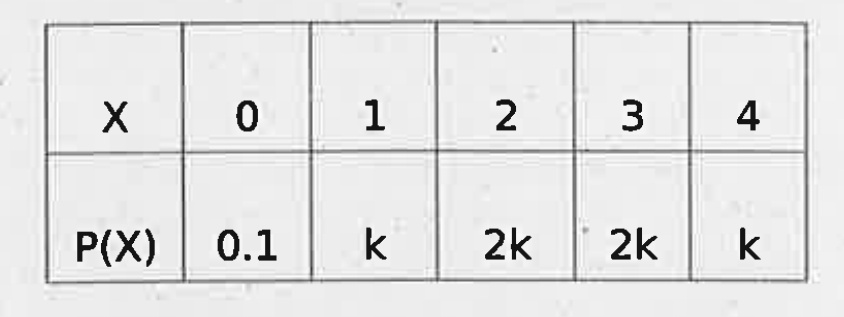
View SolutionThe probability distribution of a random variable X in given in the following table:
Find the probability that X lies between 1 and 4.
View Solution
