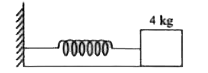
In the figure shown below , a block of mass 4 kg is attached to a spring constant 24 N/m . The coefficient og friction μ=0.5 . If the system is initially at rest and a constant horizontal force of 50 N is applied on the block , then calculate its speed when it is moved through a distance of 0.6 m .

In the presence of friction , both the spring force and frictional force will oppose the motion of the block , against the applied force .

Give , k = 24 N/m
m=4kg,μ=0.5
F=50N,x=0.6m
Work done by the two opposing forces
W1=−12kx∘−μmgx
Work done on the spring by F , W2=Fx
Net work done on the spring = Gain in K.E of block
Fx−12kx2−ugx=12mv2
50×0.6−12×24×(0.6)2−0.5×4×9.8×0.6=12×4×v2
=13.92×24=v2
v=2.64 m/s
Topper's Solved these Questions
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - PRACTICE PROBLEMS
27 Videos
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Conceptual Questions
20 Videos
- WAVESBOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions

Consider a block of mass 6 kg is attached to a spring having constant 16 Nm−1 . If the block is at rest initially and then stretched by a constant force of 20 N on frictionless surface as shown in figure . Caclculate the speed of the block when it has moved through a distance of 0.2 m from its initial position . d
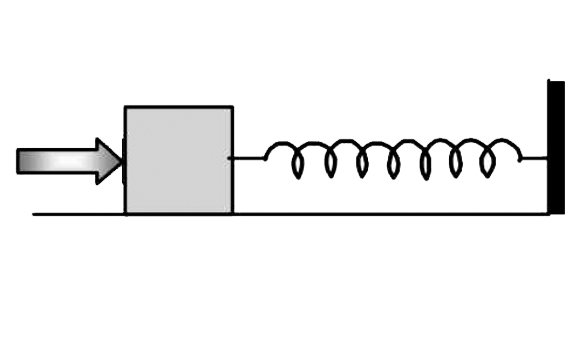
View SolutionA block of mass 4 kg while at rest is attached to an unstretched spring. The force constant of spring is 24Nm−1. If a constant horizontal force of 10 N is applied on the block, the spring gets compressed by 0.5m. What is the speed of the block at this point?
View Solution
Knowledge Check
A block of mass 5kg is lying on a rough horizontal surface. The coefficient of static and kinetic friction are 0.3 and 0.1 and 10m/s−2. If a horizontal force of 50N is applied on the block, the frictional force is
A25NB5NC10NDZeroA block A of mass 2 kg rests on another block B of mass 8 kg which rests on a horizontal floor. The coefficient of friction between A and B is 0.2 while that between B and floor is 0.5. when a horizontal force of 25 N is applied on the block B. the force of friction between A and B is
AzeroB3.9 NC5.0 ND49 NA block A of mass 2kg rests on another block B of mass 8kg which rests on a horizontal floor. The coefficient of friction between A and B is 0.2 while that between B and floor is 0.5.When a horizontal floor F of 25N is applied on the block B the force of friction between A and B is
A3NB4NC2NDzero
A spring of force constant 24N/m is resting on a frictionless horizontal surface. A force of 10N is applied on the block of mss 4kg at one end of the spring. What is the speed of the block when it has been moved through a distance of 0.5 m ?
View SolutionA block of mass 0.18kg is attached to a spring of force constant 2N/m The coefficient of friction between the block and the force is 0.1 insitially its block is at rest and the block as spring is an streched , As impalse is given to the block as shown in the figure . The block sides a distance of 0.06 in and comes to the first time . The initial velocity of the for blocks is mis V=N10 then N is .
View SolutionA block of mass 0.18kg is attached to a spring of force-constant 2N/m. The coefficient of friction between the block and the floor is 0.1 Initially the block is at rest and the spring is un-stretched. An impulse is given to the block as shown in the figure. The block slides a distance of 0.06m and comes to rest for the first time. The initial velocity of the block in m//s is V=N/10. Then N is :
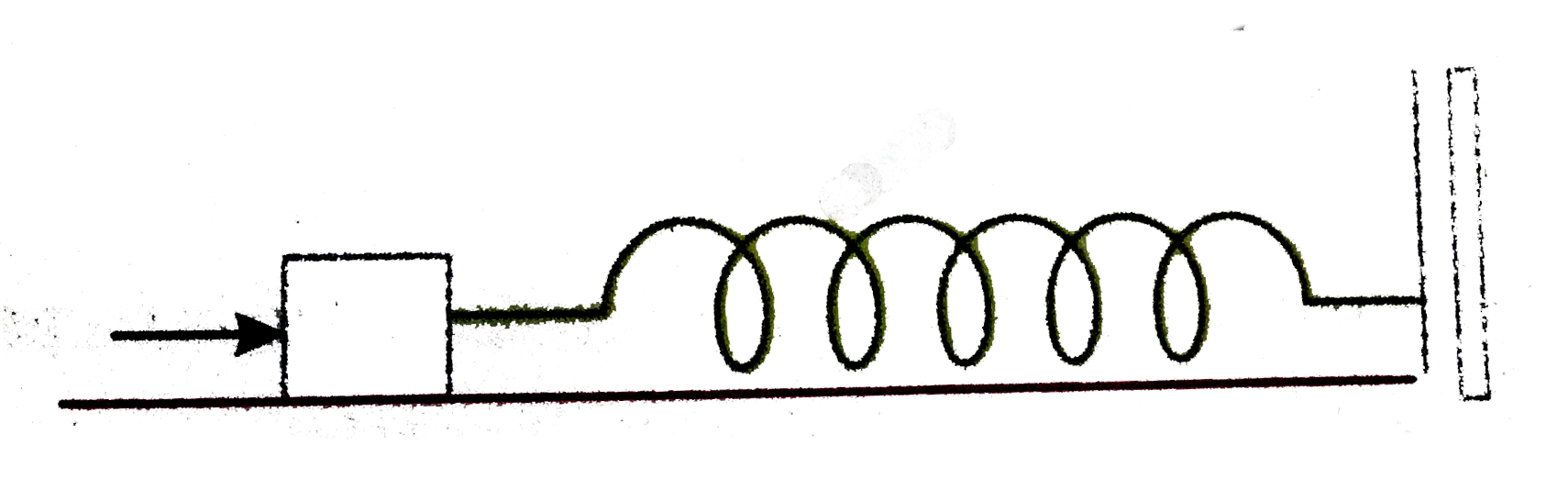 .
.
View SolutionA block of mass 2kg is connected with a spring of natural length 40cm of force constant K=200N/m. The cofficient of friction is μ=0.5. When released from the given position, acceleration of block will be

View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View Solution