A spring of force constant 24N/m is resting on a frictionless horizontal surface. A force of 10N is applied on the block of mss 4kg at one end of the spring. What is the speed of the block when it has been moved through a distance of 0.5 m ?
To solve the problem step by step, we will apply the work-energy principle and the concept of potential energy stored in the spring.
Step 1: Identify the forces acting on the block
The forces acting on the block are:
- The applied force F=10N
- The spring force Fs=kx where k=24N/m and x is the extension of the spring
- The weight of the block mg and the normal force N (which do not do work since they act perpendicular to the displacement)
Step 2: Calculate the work done by the applied force
The work done by the applied force when the block moves a distance of 0.5m is given by:
WF=F⋅d=10N⋅0.5m=5J
Step 3: Calculate the work done by the spring force
The spring force when the spring is extended by 0.5m is:
Fs=kx=24N/m⋅0.5m=12N
The work done by the spring force (which is negative since it opposes the motion) is:
Ws=−12kx2=−12⋅24N/m⋅(0.5m)2=−12⋅24⋅0.25=−3J
Step 4: Apply the work-energy theorem
According to the work-energy theorem, the change in kinetic energy (ΔKE) is equal to the total work done on the block:
ΔKE=WF+Ws
Substituting the values we calculated:
ΔKE=5J−3J=2J
Step 5: Relate change in kinetic energy to speed
The change in kinetic energy can also be expressed as:
ΔKE=12mv2−0
where m=4kg. Therefore:
2J=12⋅4kg⋅v2
This simplifies to:
2=2v2⟹v2=1⟹v=1m/s
Final Answer
The speed of the block when it has been moved through a distance of 0.5m is v=1m/s.
---
The forces acting on the block are:
- The applied force F=10N
- The spring force Fs=kx where k=24N/m and x is the extension of the spring
- The weight of the block mg and the normal force N (which do not do work since they act perpendicular to the displacement)
The work done by the applied force when the block moves a distance of 0.5m is given by:
WF=F⋅d=10N⋅0.5m=5J
The spring force when the spring is extended by 0.5m is:
Fs=kx=24N/m⋅0.5m=12N
The work done by the spring force (which is negative since it opposes the motion) is:
Ws=−12kx2=−12⋅24N/m⋅(0.5m)2=−12⋅24⋅0.25=−3J
According to the work-energy theorem, the change in kinetic energy (ΔKE) is equal to the total work done on the block:
ΔKE=WF+Ws
Substituting the values we calculated:
ΔKE=5J−3J=2J
The change in kinetic energy can also be expressed as:
ΔKE=12mv2−0
where m=4kg. Therefore:
2J=12⋅4kg⋅v2
This simplifies to:
2=2v2⟹v2=1⟹v=1m/s
The speed of the block when it has been moved through a distance of 0.5m is v=1m/s.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Conceptual Problems27videos
WORK, ENERGY AND POWER
- BOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Very Short Anwer Question.54videos
WORK, ENERGY AND POWER
- BOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Curiosity questions2videos
WORK, ENERGY AND POWER
- BOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions19videos
THERMODYNAMICS
Similar Questions
A horizontal force of 4 N is applied to a block of mass 2 kg resting on a frictionless table. What is the acceleration of the block in ms−2 ?
View SolutionA block of mass 4 kg while at rest is attached to an unstretched spring. The force constant of spring is 24Nm−1. If a constant horizontal force of 10 N is applied on the block, the spring gets compressed by 0.5m. What is the speed of the block at this point?
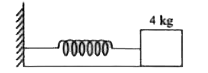 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A 30kg block rests on a rough horizontal surface A force of 200N is applied on the block The block acquires a speed of 4m/s starting from rest in 2s What is the value of coefficient of friction ? .
A√3/10B10/3C0.47D0.185 - Question 2 - Select One
Two blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig.

If the extension of the spring is x0 at time t, then the displacement of the first block at this instant isA12(Ft22m+x0)B−12(Ft22m+x0)C12(Ft22m−x0)DFt22m+x0 - Question 3 - Select One
Two blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig.

If the extension of the spring is x0 at time t, then the displacement of the second block at this instant isAFt22m−x0B12(Ft22m+x0)C12(2F2m−x0)D12(Ft22m−x0)
In the figure shown below , a block of mass 4 kg is attached to a spring constant 24 N/m . The coefficient og friction μ=0.5 . If the system is initially at rest and a constant horizontal force of 50 N is applied on the block , then calculate its speed when it is moved through a distance of 0.6 m .
 View Solution
View Solution
Consider a block of mass 6 kg is attached to a spring having constant 16 Nm−1 . If the block is at rest initially and then stretched by a constant force of 20 N on frictionless surface as shown in figure . Caclculate the speed of the block when it has moved through a distance of 0.2 m from its initial position . dView SolutionA block of mass 2.0 kg is moving on a frictionless horizontal surface with a velocity of 1.0 m/s figure towards abnother block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100 The spring constant of the spring fixed at one end is 10 N/m. Find the maximum compression of the spring.
 View Solution
View SolutionA block of mass 2 kg is moving on a frictionless horizontal surface with a velocity of 1m/s towards another block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100N/m. Find the rnaximum compression of the spring
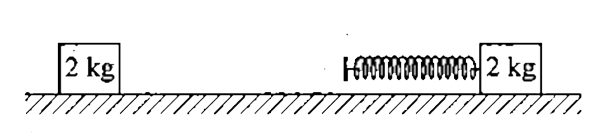 View Solution
View Solution1 kg block collides with a horizontal massless spring of force constant 2N/m. The block compresses the spring by 4m. If the coefficient of kinetic friction between the block and the· surface is 0.25, what was the speed of the block at the instant of collision? (take g=10m/s2)
 View Solution
View Solution

