Two planets have masses M and 16 M and their radii are a and 2a, respectively. The separation between the centres of the planets is 10a. A body of mass m is fired trom the surface of the larger planet towards the samller planet along the line joining their centres. For the body to be able to reach at the surface of smaller planet, the minimum firing speed needed is :
S
4√GMa
√GM2ma
32√5GMa
To solve the problem, we need to find the minimum firing speed required for a body of mass m to reach the surface of the smaller planet from the surface of the larger planet. Here's a step-by-step breakdown of the solution:
Step 1: Understanding the System
We have two planets:
- Planet 1 (larger planet) with mass M and radius a.
- Planet 2 (smaller planet) with mass 16M and radius 2a.
The distance between their centers is 10a.
Step 2: Finding the Point of Equal Gravitational Forces
When the body is fired from the larger planet, it will experience gravitational attraction from both planets. We need to find the point where the gravitational forces from both planets cancel each other out.
Let x be the distance from the center of the smaller planet where the gravitational forces balance. The distance from the center of the larger planet to this point will be 10a−x.
The gravitational force due to the larger planet at distance 10a−x is given by:
F1=GMm(10a−x)2
The gravitational force due to the smaller planet at distance x is given by:
F2=16GMmx2
Setting these forces equal to each other:
GMm(10a−x)2=16GMmx2
We can cancel GMm from both sides:
1(10a−x)2=16x2
Step 3: Cross-Multiplying and Solving for x
Cross-multiplying gives:
x2=16(10a−x)2
Expanding the right side:
x2=16(100a2−20ax+x2)
This simplifies to:
x2=1600a2−320ax+16x2
Rearranging terms:
15x2−320ax+1600a2=0
Step 4: Using the Quadratic Formula
Using the quadratic formula x=−b±√b2−4ac2a:
Here, a=15, b=−320a, and c=1600a2:
x=320a±√(−320a)2−4⋅15⋅1600a22⋅15
Calculating the discriminant:
(−320)2−4⋅15⋅1600=102400−96000=14400
Thus:
x=320a±120a30
Calculating the two possible values:
1. x=440a30=44a3
2. x=200a30=20a3
Step 5: Finding the Minimum Speed
The point where the gravitational forces cancel is at x=20a3 from the center of the smaller planet. The distance from the center of the larger planet is:
10a−20a3=30a−20a3=10a3
Step 6: Conservation of Energy
Using conservation of mechanical energy:
Initial Kinetic Energy+Potential Energy at larger planet=Potential Energy at smaller planet
12mv2−GMm10a−16GMm8a=−GMm2
Solving for v:
12mv2=GMm10a+2GMma−GMm2
Simplifying gives:
12mv2=GMm10a+20GMm10a−5GMm10a=26GMm10a
Thus:
v2=52GM10a
Taking the square root:
v=√52GM10a=2√13GM5√a
Final Answer
The minimum firing speed needed is:
v=32√5GMa
We have two planets:
- Planet 1 (larger planet) with mass M and radius a.
- Planet 2 (smaller planet) with mass 16M and radius 2a.
The distance between their centers is 10a.
When the body is fired from the larger planet, it will experience gravitational attraction from both planets. We need to find the point where the gravitational forces from both planets cancel each other out.
F1=GMm(10a−x)2
The gravitational force due to the smaller planet at distance x is given by:
F2=16GMmx2
GMm(10a−x)2=16GMmx2
We can cancel GMm from both sides:
1(10a−x)2=16x2
Cross-multiplying gives:
x2=16(10a−x)2
Expanding the right side:
x2=16(100a2−20ax+x2)
This simplifies to:
x2=1600a2−320ax+16x2
Rearranging terms:
15x2−320ax+1600a2=0
Using the quadratic formula x=−b±√b2−4ac2a:
Here, a=15, b=−320a, and c=1600a2:
x=320a±√(−320a)2−4⋅15⋅1600a22⋅15
Calculating the discriminant:
(−320)2−4⋅15⋅1600=102400−96000=14400
Thus:
x=320a±120a30
Calculating the two possible values:
1. x=440a30=44a3
2. x=200a30=20a3
The point where the gravitational forces cancel is at x=20a3 from the center of the smaller planet. The distance from the center of the larger planet is:
10a−20a3=30a−20a3=10a3
Using conservation of mechanical energy:
Initial Kinetic Energy+Potential Energy at larger planet=Potential Energy at smaller planet
12mv2−GMm10a−16GMm8a=−GMm2
Solving for v:
12mv2=GMm10a+2GMma−GMm2
Simplifying gives:
12mv2=GMm10a+20GMm10a−5GMm10a=26GMm10a
Thus:
v2=52GM10a
Taking the square root:
v=√52GM10a=2√13GM5√a
The minimum firing speed needed is:
v=32√5GMa
Topper's Solved these Questions
Similar Questions
Two stars of masses M and 4M have radii x and 3x respectively. The distance between centres of two stars is 12x. A body of mass m is fired from the surface of bigger sphere towards smaller sphere. Find the minimum initial speed (in terms of G, x, M) required to reach the surface of smaller star.
View SolutionSuppose two planets (spherical in shape) of radii R and 2R, but mass M and 9 M respectively have a centre to centre separation 8 R as shown in the figure. A satellite of mass 'm' is projected from the surface of the planet of mass 'M' directly towards the centre of the second planet. The minimum speed 'v' required for the satellite to reach the surface of the second planet is √a7GMR then the value of 'a' is ________.
[Given : The two planets are fixed in their position]
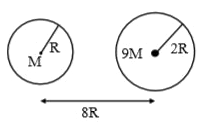
View Solution
Knowledge Check
Distance between the centres of two stars is 10a. The masses of these stars are M and 16M and their radii a and 2a respectively. A body of mass m is fired straight from the surface of the larger star towards the smaller star. The minimum initial speed for the body to reach the surface of smaller star is
A23√GmaB32√5GmaC23√5GmaD32√GmaThe distance of two planets from the sun are 1013and1012 m respectively. The ratio of the periods of the planet is
A100B1√10C√10D10√10Two planets of masses M and M2 have radii R and R2 respectively. If ratio of escape velocities from their surfaces v1v2 is n4 , then find n :
A3B1C2D4
Distance between the centres of two stars is 10a. The masses of these stars are M and 16M ans their radit a nd 2a respectively. A body of mass m is fired straight from the surface of the larger star tpwards the surface of the smaller star. What should be its minimum intial speed to reach the surface of the smaller star? Obtain the expression in terms of G, M and a.
View SolutionTwo planets A and B are at distances of 109 m and 1011m from the sun respectively. Calculate the ration of speeds of the two planets.
View SolutionThe distance between the centres of two stars is 10α. The masses of these stars are M and 16M and their radii α and 2α. A body of mass m is fired straight from the surface of the larger star towards the smaller star. What should be its minimum initial speed to reach the surface of teh smaller star? Obtain the expression interms of G, M and α.
View Solution
Two planets of mass M and 16M of radius a and 2a respectively, are at distance 10a. Find minimum speed of a particle of mass m at surface of smaller planet so that it can reached from smaller planet to larger planet.
View SolutionThe distance of the two planets from the Sun are 1013m and 1012m, respectively. Find the ratio of time periods and speeds of the two planets.
View Solution
