There is a glass sphere of radius 20 cm having refractive index 1.5. A point object is embedded inside it at a distance 6 cm to the left of the centre. Locate the image for observer looking from left. Locate the image for observer looking from right.
To solve the problem of locating the image formed by a glass sphere with a point object embedded in it, we will use the formula for refraction through spherical surfaces. Let's break down the solution step by step for both observers (from the left and from the right).
Step 1: Understand the Setup
- We have a glass sphere with a radius R=20cm and a refractive index n1=1.5 (for glass).
- The refractive index of air (outside the sphere) is n2=1.0.
- The point object is located 6cm to the left of the center of the sphere.
Step 2: Determine Object Distance for Observer on the Left
- The center of the sphere is at 0cm. Therefore, the object distance u for the observer looking from the left is:
u=−14cm(since the object is 6 cm to the left of the center, total distance from the center is 20−6=14cm)
Step 3: Apply the Refraction Formula for Observer on the Left
Using the formula:
n2v−n1u=n2−n1R
Substituting the values:
- n2=1.0
- n1=1.5
- u=−14cm
- R=−20cm
The equation becomes:
1v−1.5−14=1−1.5−20
Step 4: Simplify the Equation
Rearranging gives:
1v+1.514=−0.5−20
Calculating the right side:
1v+1.514=0.520=140
Step 5: Solve for v
Now, we can find v:
1v=140−1.514
Finding a common denominator (280):
1v=7−30280=−23280
Thus,
v=−28023≈−12.17cm
Step 6: Locate the Image Position for Observer on the Left
The negative sign indicates that the image is virtual and located on the same side as the object. The distance from the center of the sphere is:
20−12.17≈7.83cm
Step 7: Determine Object Distance for Observer on the Right
For the observer looking from the right, the object appears at:
u=−26cm(since the total distance is 20+6=26cm)
Step 8: Apply the Refraction Formula for Observer on the Right
Using the same formula:
1v−1.5−26=1−1.5−20
This simplifies to:
1v+1.526=0.520
Step 9: Solve for v
Rearranging gives:
1v=140−1.526
Finding a common denominator (520):
1v=13−30520=−17520
Thus,
v=−52017≈−30.6cm
Step 10: Locate the Image Position for Observer on the Right
The negative sign indicates that the image is also virtual. The distance from the center of the sphere is:
20−30.6≈−10.6cm(which means the image is 10.6 cm to the left of the center)
Summary of Results
- For the observer looking from the left, the image is located approximately 7.83cm to the right of the center of the sphere.
- For the observer looking from the right, the image is located approximately 10.6cm to the left of the center of the sphere.
- We have a glass sphere with a radius R=20cm and a refractive index n1=1.5 (for glass).
- The refractive index of air (outside the sphere) is n2=1.0.
- The point object is located 6cm to the left of the center of the sphere.
- The center of the sphere is at 0cm. Therefore, the object distance u for the observer looking from the left is:
u=−14cm(since the object is 6 cm to the left of the center, total distance from the center is 20−6=14cm)
Using the formula:
n2v−n1u=n2−n1R
Substituting the values:
- n2=1.0
- n1=1.5
- u=−14cm
- R=−20cm
1v−1.5−14=1−1.5−20
Rearranging gives:
1v+1.514=−0.5−20
Calculating the right side:
1v+1.514=0.520=140
Now, we can find v:
1v=140−1.514
Finding a common denominator (280):
1v=7−30280=−23280
Thus,
v=−28023≈−12.17cm
The negative sign indicates that the image is virtual and located on the same side as the object. The distance from the center of the sphere is:
20−12.17≈7.83cm
For the observer looking from the right, the object appears at:
u=−26cm(since the total distance is 20+6=26cm)
Using the same formula:
1v−1.5−26=1−1.5−20
This simplifies to:
1v+1.526=0.520
Rearranging gives:
1v=140−1.526
Finding a common denominator (520):
1v=13−30520=−17520
Thus,
v=−52017≈−30.6cm
The negative sign indicates that the image is also virtual. The distance from the center of the sphere is:
20−30.6≈−10.6cm(which means the image is 10.6 cm to the left of the center)
- For the observer looking from the left, the image is located approximately 7.83cm to the right of the center of the sphere.
- For the observer looking from the right, the image is located approximately 10.6cm to the left of the center of the sphere.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Revision Exercises (Very Short Answer Questions)82videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Revision Exercises (Additional Questions)22videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - NCERT (Exemplar Problems Subjective Questions) (Very Short Answer Type Questions)11videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION15videos
NUCLEI
- BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION12videos
SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS
Similar Questions
The base of a rectangular glass slab of thickness 10 cm and refractive index 1.5 is silvered. A coloured spot inside the glass slab at a distance of 8 cm from the base. Determine the position of the image formed by the mirror as observed from the top.
View SolutionA small object is embedded in a glass sphere (mu =1.5) of radius 5.0 cm at a distance 1.5 cm left to the centre. Locate the image of the object as seen by an observer standing (a) to the left of the sphere and (b) to the right of the sphere.
View Solution
Knowledge Check
- Question 1 - Select One
A point object is placed at the centre of a glass sphere of radius 6 cm and refractive index 1.5. The distance of the virtual image from the surface of the glass is
A2 cmB4 cmC6 cmD12 cm - Question 2 - Select One
In a medium of refractive index 1.6 and having a convex surface has a point object in it at a distance of 12 cm from the pole. The radius of curvature is 6 cm. Locate the image as seen from air
AA real image at 30 cmBA virtual image at 30 cmCA real image at 4.28 cmDA virtual image at 4.28 cm - Question 3 - Select One
A point object is situated at a distance of 36 cm from the centre of the sphere of radius 12 cm and refractive index 1.5. Locate the position of the image due to refraction through sphere.
A24 cm from the surfaceB36 cm from the centreC24 cm from the centreDBoth (1) & (2)
There is a glass (μ=1.5) biconvex lens of radius of curvature 5 cm and thickness of the lens is also 5 cm. An object is placed at a distance 20 cm from the front surface of lens. Locate its final image.
View SolutionA small air bubble O (as shown in figure) is formed inside the solid glass sphere of radius 10 cm. The refractive index of glass μ=32. The position of air at distance 5 cm from centre. If one half of sphere is polished. Then find the distance between images seen by observer on the left side of sphere. Assume μ=1.5.
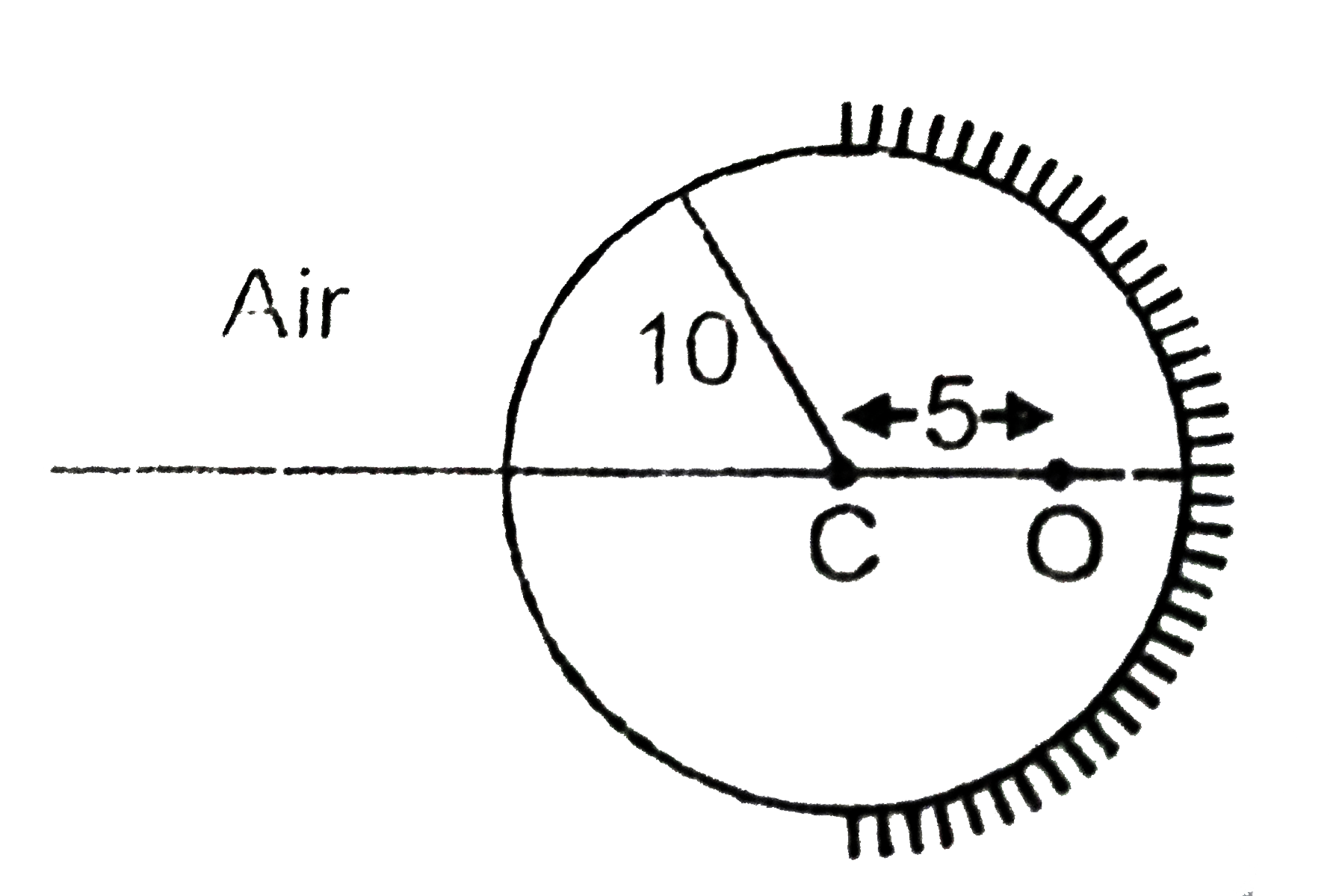 View Solution
View SolutionAn object is placed at a distance of 6cm from a convex mirror of focal length 20cm. Locate the position and nature of the image.
View SolutionAn image is formed at a distance of 100 cm from the glass surface with refractive index 1.5, when a point object is placed in the air at a distance of 100 cm from the glass surface. The radius of curvature is of the surface is
View SolutionA point object is placed at a distance 20 cm from the focus of a concave mirror of radius of curvature 20 cm. Find the distance (in cm) of the image from the focus.
View Solution

