If we turn the mirror by an angle of 20∘, the reflected ray will turn through which angle ?
To solve the problem of how much the reflected ray will turn when the mirror is turned by an angle of 20∘, we can follow these steps:
1. Understand the Setup:
- We have a mirror and an incident ray striking the mirror.
- When the mirror is turned by an angle θ, the normal to the mirror surface also shifts by the same angle.
2. Initial Angles:
- Let the angle of incidence be I and the angle of reflection be R. According to the law of reflection, I=R.
3. Turning the Mirror:
- When the mirror is turned by an angle θ=20∘, the new angle of incidence becomes I+θ (since the incident ray remains the same, but the mirror's orientation changes).
4. New Reflection Angle:
- The new angle of reflection will also change. The angle of reflection will now be R′=I+θ (because the law of reflection still holds).
5. Calculating the Change in Angle:
- The change in the angle of reflection, denoted as ϕ, can be calculated as follows:
- Initially, the angle of reflection was R.
- After turning the mirror, the new angle of reflection is R′=I+θ.
- Since I=R, we can substitute to find R′=R+θ.
6. Finding the Total Turn of the Reflected Ray:
- The total turn of the reflected ray is given by:
ϕ=R′−R=(I+θ)−I=θ
- Therefore, the reflected ray will turn through an angle of 2θ (since both the angle of incidence and angle of reflection change).
7. Final Calculation:
- Substituting θ=20∘:
ϕ=2×20∘=40∘
Conclusion:
The reflected ray will turn through an angle of 40∘.
- We have a mirror and an incident ray striking the mirror.
- When the mirror is turned by an angle θ, the normal to the mirror surface also shifts by the same angle.
- Let the angle of incidence be I and the angle of reflection be R. According to the law of reflection, I=R.
- When the mirror is turned by an angle θ=20∘, the new angle of incidence becomes I+θ (since the incident ray remains the same, but the mirror's orientation changes).
- The new angle of reflection will also change. The angle of reflection will now be R′=I+θ (because the law of reflection still holds).
- The change in the angle of reflection, denoted as ϕ, can be calculated as follows:
- Initially, the angle of reflection was R.
- After turning the mirror, the new angle of reflection is R′=I+θ.
- Since I=R, we can substitute to find R′=R+θ.
- The total turn of the reflected ray is given by:
ϕ=R′−R=(I+θ)−I=θ
- Therefore, the reflected ray will turn through an angle of 2θ (since both the angle of incidence and angle of reflection change).
- Substituting θ=20∘:
ϕ=2×20∘=40∘
The reflected ray will turn through an angle of 40∘.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Revision Exercises (Additional Questions)
22 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Revision Exercises (Fill in the Blanks)
10 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Higher Order Thinking Skills & Advanced Level (QUESTIONS WITH ANSWERS)
20 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
12 Videos
Similar Questions
A ray of light is incident on a plane mirror placed horizontally. When the mirror is rotated through an angle 30∘ the reflected ray is found to be directed along the vertical. Determine the angle of incidence at the initial position of the mirror.
View SolutionIn the given figure, two mirrors X and Y are situated at an angle of 60∘ with each other and a ray of light is incident on mirror X at an angle of 50∘. When the ray is reflected by the mirror Y, then what is angle of reflection at this mirror?

View Solution
Knowledge Check
A ray of light strikes a silvered surface inclined to another one at an angle of 90∘. Then the reflected ray will turn through
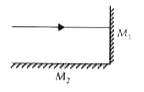 A0∘B45∘C90∘D180∘
A0∘B45∘C90∘D180∘When a plane mirror is rotated through an angle θ then the reflected ray turns through the angle 2θ then the size of the image
AIs doubledBIs halvedCRemins the sameDBecomes infiniteWhen a mirror is rotated by a angle θ , the reflected ray will rotated by
A0∘Bθ/2CθD2θ
When a light ray is incident normally on the surface of a plane mirror, the reflected ray deviates through an angle of ________
View SolutionFor a fixed incident light ray, if the mirror be rotated through and angle θ (about an axis which lies in the plane of mirror and perpendicular to the plane of incidence), show that the reflected ray turns through an angle 2θ in same sense.
View SolutionWhen a ray of light strikes a plane mirror at an angle of 15∘ with the mirror, what will be the angle through which the ray gets deviated?

View SolutionWhen mirror is rotated through an angle θ, a reflected ray from it moves through an angle of
View SolutionA ray of light is incident on a plane mirror at an angle of 20∘ with the normal, at the point of incidence, Through what angle, the ray of light will be deviated from its direction of incidence ?
View Solution
