For a light ray passing through a prism
angle of deviation increases when angle of incidence is increased
angle of deviation decreases when angle of deviation is increased
When angle of incidence is increased or decreased from a particular value then in both cases angle of deviation increases.
Angle of deviation is approximately proportional to the refracting angle of prism provided prism is very thin.
The correct Answer is:C, D
To solve the question regarding the behavior of a light ray passing through a prism, we will analyze the relationship between the angle of incidence and the angle of deviation.
1. Understanding the Prism:
- A prism is a transparent optical element with flat, polished surfaces that refract light. The angle between the two plane surfaces of the prism is called the refracting angle (A).
2. Angle of Incidence (i):
- The angle of incidence is the angle at which the incoming light ray strikes the surface of the prism.
3. Angle of Deviation (D):
- The angle of deviation is the angle between the original path of the light ray and its path after passing through the prism.
4. Behavior of Angle of Deviation:
- When the angle of incidence increases from a small value, the angle of deviation initially decreases until it reaches a minimum value at a certain angle of incidence (let's call this angle i_min).
- Beyond this minimum angle of incidence, as the angle of incidence continues to increase, the angle of deviation starts to increase again.
5. Analyzing the Options:
- Option A: "The angle of deviation increases when the angle of incidence is increased."
- This is only true for the range after the minimum angle of incidence, so it is not universally correct.
- Option B: "The angle of deviation decreases when the angle of incidence is increased."
- This is also not universally correct as it only holds true until the minimum angle of incidence.
- Option C: "The angle of deviation increases when the angle of incidence is increased or decreased from a particular value."
- This option is correct because, after reaching the minimum angle, any increase or decrease from that angle will lead to an increase in the angle of deviation.
- Option D: "The angle of deviation is approximately proportional to the refracting angle of the prism."
- This is also correct, especially for thin prisms, as the angle of deviation can be expressed in terms of the refracting angle.
6. Conclusion:
- The correct options are C and D.
- A prism is a transparent optical element with flat, polished surfaces that refract light. The angle between the two plane surfaces of the prism is called the refracting angle (A).
- The angle of incidence is the angle at which the incoming light ray strikes the surface of the prism.
- The angle of deviation is the angle between the original path of the light ray and its path after passing through the prism.
- When the angle of incidence increases from a small value, the angle of deviation initially decreases until it reaches a minimum value at a certain angle of incidence (let's call this angle i_min).
- Beyond this minimum angle of incidence, as the angle of incidence continues to increase, the angle of deviation starts to increase again.
- Option A: "The angle of deviation increases when the angle of incidence is increased."
- This is only true for the range after the minimum angle of incidence, so it is not universally correct.
- Option B: "The angle of deviation decreases when the angle of incidence is increased."
- This is also not universally correct as it only holds true until the minimum angle of incidence.
- Option C: "The angle of deviation increases when the angle of incidence is increased or decreased from a particular value."
- This option is correct because, after reaching the minimum angle, any increase or decrease from that angle will lead to an increase in the angle of deviation.
- Option D: "The angle of deviation is approximately proportional to the refracting angle of the prism."
- This is also correct, especially for thin prisms, as the angle of deviation can be expressed in terms of the refracting angle.
- The correct options are C and D.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - OBJECTIVE TYPE QUESTIONS (D. MULTIPLE CHOICE QUESTIONS)
5 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS)
10 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - OBJECTIVE TYPE QUESTIONS (JEE (ADVANCED) FOR IIT ENTRANCE)
20 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
12 Videos
Similar Questions
Plot a graph to show the variation of the angle of deviation as a function of angle of incidence for light rays passing through a prism. Write the relation for the refractive index of the prism in terms of the angle of minimum deviation and the angle of the prism.
View SolutionDraw the path of light ray passing through a prism. Label angle of incidence and angle of deviation in the ray diagram.
View Solution
Knowledge Check
A horizontal light ray passes through a prism (μ=1.5) of angle 4∘.Further, it is incident on a plane mirror M, that has been placed verticall. By what angle the mirror is rotated so that the ray after reflection becomes horizontal?
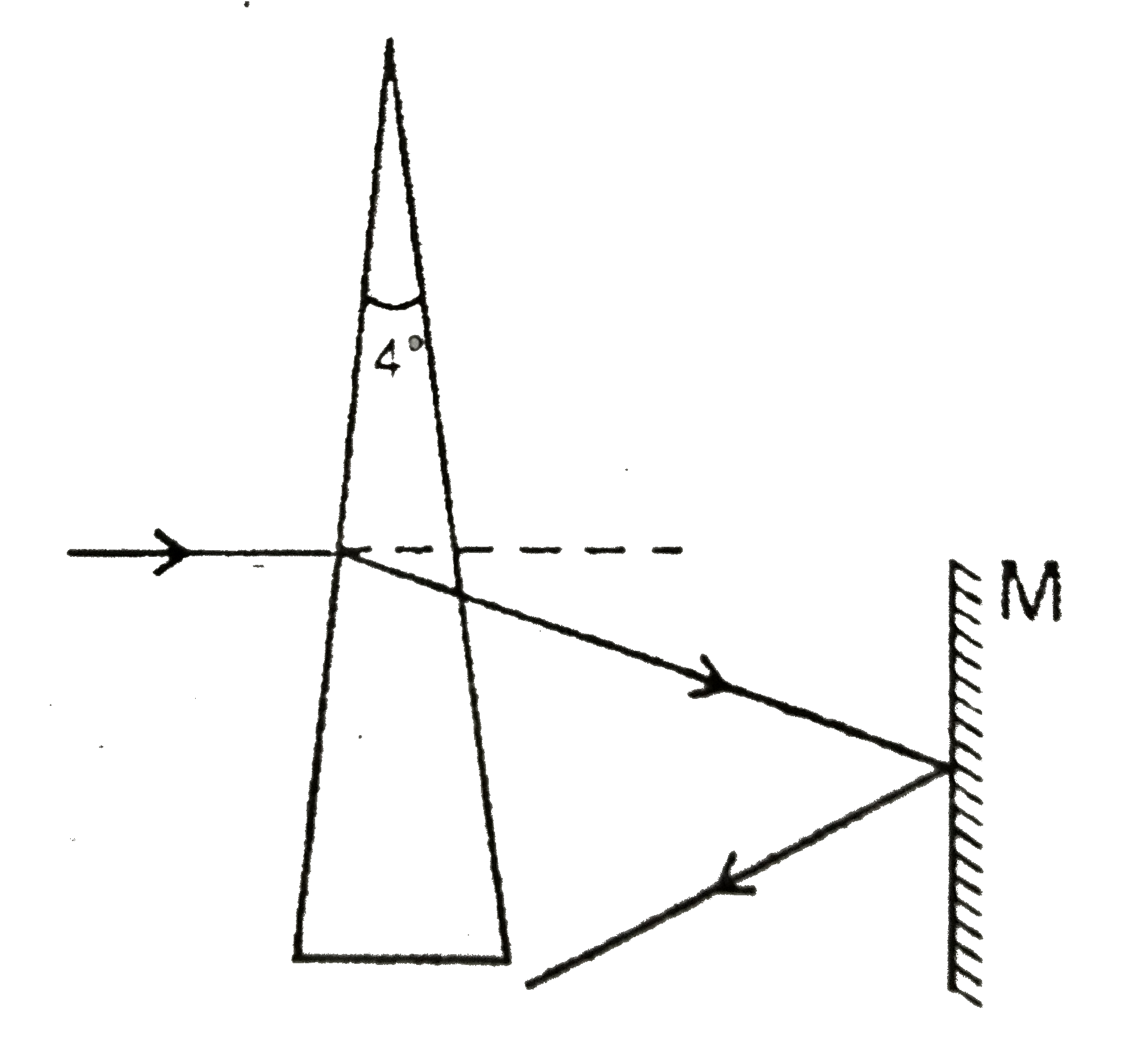 A1∘B2∘C4∘D8∘
A1∘B2∘C4∘D8∘The path of light rays passing through a glass prism is BEST represented by ________
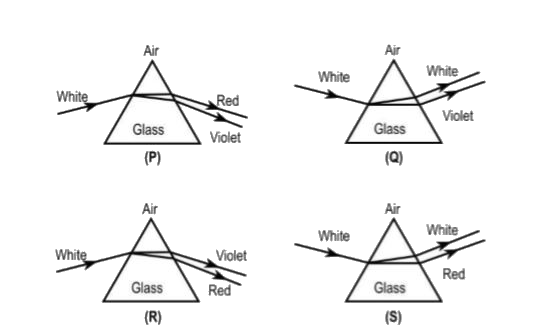 Aonly PBonly RCeither Q or SDeither P or R
Aonly PBonly RCeither Q or SDeither P or RA ray of light passing through a prism of refracting angle 60∘ has to deviate by at least 40∘. Then refractive index of prism should be
A≤√2B<√2C<1D≥1
Find the minimum and maximum deflectrion angls for a light ray passing through a glass prism with refracting angle θ=60∘.
View SolutionWhat is the cause of dispersion of light on passing through a prism ?
View SolutionWhy does a ray of light while passing through a prism, bend towards its base?
View SolutionA ray of light passing through a prism (μ=√3)suffers minimum deviation. It is found that the angle of incidence is double the angle of refraction within the prism. Then, the angle of prism is ________ (in degrees)
View SolutionA ray of light passing through a prism of refraction angle 60∘ has to deviate by atleast 30∘. Then, refractive index of prism should be
View Solution
